Автор: Денис Аветисян
Новая теория объясняет внезапные и сильные колебания цен на финансовых рынках как кратковременные, но мощные изменения в динамике ценообразования.

В статье представлена гипотеза о ‘всплесках дрифта’ как причине устойчивых ценовых движений, связанных с микроструктурой рынка и описываемых стохастическими процессами Ито.
Несмотря на развитые модели ценообразования, внезапные и кратковременные обвалы на финансовых рынках остаются сложной проблемой. В работе, посвященной ‘The drift burst hypothesis’, предложена концепция кратковременных взрывов дрейфа, объясняющих устойчивые ценовые движения, подобные флэш-крахам. Показано, что такие “всплески дрейфа” являются регулярным явлением на различных активах — от акций до валют — и связаны с особенностями микроструктуры рынка. Может ли понимание динамики этих всплесков привести к более эффективным стратегиям управления рисками и прогнозирования экстремальных событий на финансовых рынках?
Разоблачение скрытых факторов обвалов рынка
Традиционные модели анализа финансовых рынков зачастую оказываются неспособными в полной мере объяснить динамику стремительных обвалов, таких как «флэш-креши». Это несоответствие указывает на существенные пробелы в понимании экстремальных событий, происходящих на рынке. Существующие подходы, как правило, хорошо справляются с описанием постепенных изменений, однако не учитывают специфику внезапных и кратковременных ценовых скачков, которые могут кардинально изменить ситуацию. Неспособность адекватно отразить эти явления ограничивает возможности прогнозирования и управления рисками, что особенно критично в условиях высокой волатильности и непредсказуемости современной финансовой системы. Поэтому необходим пересмотр существующих методологий и разработка новых подходов, способных более точно моделировать поведение рынка в экстремальных ситуациях.
Неспособность традиционных моделей адекватно объяснить стремительные падения рынка, такие как флэш-креши, обусловлена неполным учетом кратковременных, но интенсивных ценовых колебаний, получивших название “всплески дрифта”. Эти эпизоды характеризуются резким и неожиданным изменением цены, которое может значительно искажать стандартные аналитические показатели и приводить к ошибочным выводам. Всплески дрифта, будучи локальными и быстротечными явлениями, зачастую не связаны с фундаментальными изменениями в стоимости активов, что делает их особенно сложными для прогнозирования и требует разработки новых методов анализа, способных улавливать эти мимолетные, но значимые движения.
Изучение этих кратковременных ценовых всплесков представляется критически важным, поскольку они отражают локально взрывные явления, которые могут быть оторваны от фундаментальной стоимости активов. В отличие от постепенных изменений, обусловленных макроэкономическими факторами или новостями о компаниях, подобные всплески способны формировать динамику рынка, не имея прочной связи с реальными экономическими показателями. Это означает, что традиционные модели оценки, основанные на фундаментальном анализе, могут оказаться неэффективными при прогнозировании и управлении рисками, связанными с подобными событиями. Понимание механизмов, лежащих в основе этих всплесков, позволяет выявить потенциальные точки нестабильности и разработать более надежные стратегии защиты от внезапных и непредсказуемых рыночных колебаний.
Непредсказуемость этих внезапных скачков цен представляет собой серьезную проблему для существующих моделей анализа рынков. Традиционные методы, основанные на предположении о постепенном изменении стоимости активов, оказываются неэффективными при столкновении с кратковременными, но интенсивными всплесками, которые могут искажать общую картину. Для точного выявления и оценки влияния этих явлений необходимы принципиально новые аналитические инструменты, способные фиксировать и интерпретировать столь мимолетные изменения. Эти инструменты должны учитывать нелинейность процессов и учитывать, что такие всплески могут возникать независимо от фундаментальной стоимости активов, что делает их прогнозирование особенно сложным. Разработка таких инструментов является ключевым шагом к повышению устойчивости финансовых рынков и предотвращению внезапных обвалов.

Моделирование невидимого: высокочастотные данные и снижение шума
Анализ микроструктуры рынка требует использования данных с высокой частотой (HighFrequencyData), представляющих собой записи изменений цен на максимально детализированном уровне. Эти данные фиксируют каждую транзакцию и котировку, обеспечивая возможность изучения поведения участников рынка и динамики цен в режиме реального времени. В отличие от традиционных данных, агрегированных по более крупным временным интервалам, HighFrequencyData позволяют выявить закономерности, скрытые в краткосрочных колебаниях цен, и оценить влияние различных факторов, таких как ордера и заявки, на формирование цены актива. Для получения таких данных используются специализированные системы сбора и обработки информации, способные фиксировать события в масштабе миллисекунд или даже микросекунд.
Высокочастотные данные, необходимые для анализа микроструктуры рынка, подвержены внутреннему шуму, известному как “микроструктурный шум”. Этот шум возникает из-за процессов исполнения ордеров и активности участников рынка, включающих в себя несинхронность котировок, дискретность цен, а также влияние ордеров на покупку и продажу, которые не отражают истинные изменения в цене. В частности, ордера, исполняемые не мгновенно, и ограниченность глубины книги ордеров вносят вклад в искажение наблюдаемых цен, создавая случайные колебания, которые необходимо учитывать при анализе данных. Игнорирование микроструктурного шума может привести к неверной интерпретации рыночных сигналов и ошибочным выводам относительно эффективности и ликвидности рынка.
Предварительное усреднение (Pre-Averaging) является важным начальным этапом снижения шума в высокочастотных данных, возникающего из-за микроструктуры рынка. Этот метод предполагает расчет среднего значения цены за определенный интервал времени, что позволяет сгладить краткосрочные колебания, вызванные порядками на исполнение и активностью участников. Важно отметить, что предварительное усреднение стремится к минимизации шума без существенной потери информации о реальных изменениях цены, сохраняя основные характеристики данных для последующего анализа. Эффективность данного метода напрямую зависит от правильно подобранного интервала усреднения, определяющего степень сглаживания.
Эффективный выбор ширины полосы пропускания (bandwidth selection) является критически важным этапом в процессе сглаживания высокочастотных данных. Этот параметр, определяющий степень усреднения, напрямую влияет на баланс между снижением шума микроструктуры и сохранением полезного сигнала. Слишком малая ширина полосы приведет к недостаточному подавлению шума, а слишком большая — к избыточному сглаживанию и потере информации о реальных ценовых изменениях. Оптимальная ширина полосы определяется с использованием различных методов, включая кросс-валидацию и методы, основанные на асимптотической минимизации смещения, с целью достижения наилучшего компромисса между дисперсией и смещением оценки. Выбор ширины полосы также может зависеть от конкретных характеристик данных и целей анализа, например, от необходимости точного определения волатильности или выявления краткосрочных трендов.
Ядерная оценка: раскрытие динамики цен
Ядерная оценка (Kernel Estimation) представляет собой непараметрический метод моделирования динамики цен, позволяющий избежать наложения жестких предположений о базовом распределении данных. В отличие от параметрических моделей, требующих определения фиксированного числа параметров для описания распределения, ядерная оценка строит функцию плотности вероятности непосредственно из наблюдаемых данных, используя ядра — весовые функции, определяющие вклад каждого наблюдения в итоговую оценку. Гибкость метода позволяет адаптироваться к различным формам распределения цен, включая те, которые не соответствуют стандартным параметрическим моделям, таким как нормальное или экспоненциальное распределение. Это особенно важно при анализе финансовых временных рядов, характеризующихся ненормальностью и наличием «толстых хвостов».
Различные функции ядра, такие как ‘ExponentialKernel’ и ‘ParzenKernel’, обеспечивают различную степень сглаживания при оценке плотности вероятности. ‘ExponentialKernel’ характеризуется экспоненциальным убыванием весов, что приводит к более быстрому снижению влияния удаленных точек данных и, как следствие, к менее сглаженной оценке. ‘ParzenKernel’, напротив, использует полиномиальное убывание весов, обеспечивая более плавную и сглаженную оценку плотности. Выбор конкретной функции ядра определяется характеристиками анализируемых данных; для данных с выраженными выбросами предпочтительнее ядра с более быстрым убыванием весов, в то время как для данных с небольшим уровнем шума может быть достаточно ядер, обеспечивающих более высокую степень сглаживания.
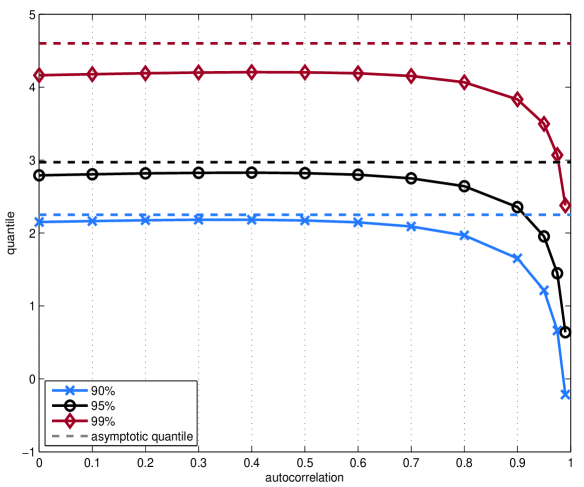
Надежность оценок, полученных с использованием Kernel Estimation, обеспечивается последовательной коррекцией ошибок посредством применения ‘HACEstimator’. Данный инструмент предназначен для учета гетероскедастичности и автокорреляции, часто встречающихся в финансовых временных рядах. Гетероскедастичность подразумевает непостоянство дисперсии ошибки, а автокорреляция — зависимость между последовательными значениями ошибки. ‘HACEstimator’ корректирует стандартные ошибки оценок, учитывая эти факторы, что позволяет получить более точные и достоверные результаты анализа и избежать ошибочных выводов о статистической значимости полученных параметров.
Точность оценок, получаемых с помощью ‘HACEstimator’, базируется на теоретических свойствах распределения Гумбеля. Данное распределение применяется для моделирования экстремальных значений, часто встречающихся во временных рядах финансовых данных. Распределение Гумбеля описывает вероятность появления максимальных или минимальных значений в последовательности наблюдений, что критически важно для корректной оценки гетероскедастичности и автокорреляции, учитываемых ‘HACEstimator’. Использование распределения Гумбеля позволяет более адекватно оценивать дисперсию оценок и обеспечивать их статистическую значимость, особенно при анализе периодов высокой волатильности на финансовых рынках. F(x) = exp(-exp(-(x - \mu) / \beta)) — основная функция распределения Гумбеля, где μ — параметр местоположения, а β — параметр масштаба.
Модель Хестона и далее: улавливая сложную динамику
Модель Хестона, представляющая собой стохастическую модель волатильности, обеспечивает мощную основу для включения в анализ процессов, связанных с волатильностью и скачкообразными изменениями. В отличие от традиционных моделей, предполагающих постоянную волатильность, модель Хестона рассматривает волатильность как случайный процесс, подверженный собственным колебаниям. Это позволяет более реалистично отражать динамику финансовых рынков, где волатильность не является фиксированной величиной, а изменяется во времени. Кроме того, модель позволяет интегрировать скачкообразные процессы, что необходимо для адекватного описания резких и неожиданных изменений цен, не объясняемых непрерывными колебаниями. Использование модели Хестона позволяет исследователям и практикам лучше понимать и прогнозировать поведение финансовых активов, а также эффективно управлять рисками, связанными с волатильностью и экстремальными событиями.
Расширение модели Хестона за счет включения процесса скачкообразной диффузии позволяет учесть внезапные, разрывные изменения цен, часто сопровождающие периоды “дрифтовых всплесков”. Традиционная модель Хестона, описывающая стохастическую волатильность, не в полной мере отражает резкие скачки, характерные для финансовых рынков. Интеграция скачкообразного процесса, добавляющего возможность мгновенных изменений цены, значительно повышает реалистичность модели и её способность адекватно описывать динамику активов в периоды интенсивных ценовых движений. Это особенно важно при анализе экстремальных событий и построении более точных моделей ценообразования, поскольку позволяет учесть влияние внезапных шоков на волатильность и доходность.
Точность моделирования динамики цен значительно возрастает при использовании данных высокой частоты для калибровки и валидации. Анализ, основанный на данных, собранных с высокой временной разрешаемостью, позволяет более детально оценить параметры модели, включая скорость и волатильность, а также выявить закономерности, которые остаются незамеченными при использовании менее детализированных данных. Такой подход позволяет более реалистично воспроизводить поведение финансовых инструментов, особенно в периоды повышенной волатильности и резких изменений цен, что критически важно для точной оценки рисков и прогнозирования будущих движений рынка. Использование данных высокой частоты не только улучшает точность модели, но и позволяет выявлять ранее неизвестные особенности динамики цен, открывая новые возможности для анализа и принятия инвестиционных решений.
Исследование показало, что резкие изменения в динамике цен, известные как “drift bursts”, являются устойчивой характеристикой финансовых рынков, а не случайными отклонениями. Регрессионный анализ, проведенный на различных классах активов, выявил значимую взаимосвязь между доходностью, предшествующей “drift burst”, и доходностью, следующей за ним. Коэффициент детерминации R^2 в этом анализе составил от 25% до 40%, что свидетельствует о существенной предсказательной силе данного явления. Это указывает на то, что, анализируя предшествующую динамику цен, можно с определенной вероятностью прогнозировать последующее поведение рынка после возникновения “drift burst”, что открывает новые возможности для разработки более точных моделей ценообразования и управления рисками.
Анализ выявленных скачков дрифта показал, что приблизительно в 65% случаев за ними следует разворот цены, что указывает на выраженную тенденцию к возвращению к среднему значению. Данное наблюдение подчеркивает, что экстремальные движения, вызванные скачками дрифта, не являются устойчивыми и часто сменяются коррекцией. Вероятность разворота цены после скачка дрифта является значительной, что позволяет предположить, что рынок обладает определенной степенью саморегуляции и стремится к равновесию. Такая динамика имеет существенное значение для моделирования ценовых процессов и оценки рисков, поскольку указывает на возможность использования стратегий, основанных на возвращении к среднему, для получения прибыли или смягчения потерь.
Анализ регрессии подтверждает наличие отрицательного и статистически значимого коэффициента для доходности после возникновения скачка дрейфа, что указывает на последовательное снижение цены после таких событий. Данный результат демонстрирует, что скачки дрейфа не являются случайными, а предвещают коррекцию цены. Наблюдаемая тенденция к снижению после скачка дрейфа предполагает, что эти события часто приводят к переоценке актива, за которой следует возврат к более фундаментальному уровню. Подобная закономерность позволяет использовать информацию о скачках дрейфа для прогнозирования краткосрочных ценовых движений и разработки более эффективных стратегий управления рисками, учитывающих склонность к возврату цены к среднему после периодов аномального роста.
Предложенный подход позволяет получить более глубокое понимание гипотезы о скачках цены (Drift Burst Hypothesis) и её последствий для моделирования экстремальных событий на финансовых рынках. Вместо рассмотрения цены как непрерывного процесса, модель учитывает внезапные и значительные изменения, называемые “скачками”, которые оказывают существенное влияние на последующую динамику. Анализ данных показал, что эти скачки не являются случайными, а имеют предсказуемые характеристики, включая отрицательную корреляцию между возвратом до скачка и возвратом после него. Это позволяет не только точнее описывать прошлые движения цены, но и улучшить прогнозы будущих экстремальных событий, что особенно важно для управления рисками и разработки эффективных стратегий торговли. Подобный подход открывает новые возможности для понимания механизмов формирования цен и повышения устойчивости финансовых систем к неожиданным шокам.

Исследование, представленное в данной работе, напоминает о неизбежности изменений в любой системе, даже в такой сложной, как финансовый рынок. Гипотеза о «всплесках дрифта» предполагает, что кажущиеся аномальными скачки цен — это не отклонения от нормы, а кратковременные проявления внутренней динамики. Это созвучно мысли Марии Уоллстонкрафт: «Невозможно создать что-то совершенное, если не признать, что всё подвержено изменениям». Именно признание этой изменчивости, понимание того, что даже самые стабильные системы могут подвергаться внезапным и интенсивным колебаниям, позволяет разрабатывать более эффективные стратегии управления рисками и понимать природу волатильности, особенно в контексте высокочастотной торговли и микроструктуры рынка.
Что впереди?
Предложенная гипотеза о «всплесках дрифта» лишь фиксирует закономерность, а не объясняет ее первопричину. Каждая архитектура финансовых систем проживает свой срок, и наблюдение за кратковременными, но интенсивными изменениями коэффициента дрифта — это скорее констатация факта старения, нежели предсказание будущего. Попытки «поймать» эти всплески, безусловно, будут предприниматься, но следует помнить: улучшения в алгоритмах высокочастотной торговли стареют быстрее, чем мы успеваем их понять.
Необходимо углубить понимание взаимосвязи между микроструктурой рынка и возникновением этих “всплесков”. Вопросы о роли ликвидности, ордерного потока и поведения маркет-мейкеров остаются открытыми. Важно учитывать, что даже наиболее точные математические модели — лишь приближения к сложной реальности, и их применение в динамично меняющейся среде всегда сопряжено с риском.
Исследование импульсных процессов, подобных описанным, неизбежно наталкивается на проблему определения «нормы». Что есть стабильность, если все системы подвержены энтропии? Возможно, будущее за изучением не самих «всплесков», а механизмов восстановления после них — способности рынка к саморегуляции и адаптации. Все, в конечном счете, возвращается к вопросу о жизнеспособности, а не о совершенстве.
Оригинал статьи: https://arxiv.org/pdf/2601.08974.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- MYX ПРОГНОЗ. MYX криптовалюта
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- SOL ПРОГНОЗ. SOL криптовалюта
- ПРОГНОЗ ДОЛЛАРА К ЗЛОТОМУ
- Золото прогноз
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
2026-01-15 21:19