Укрощение высокочастотных данных: новый подход к оценке волатильности

Автор: Денис Аветисян

В статье представлен эффективный метод анализа данных с высокой частотой, позволяющий получать более точные оценки волатильности даже в условиях шума и скачков.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал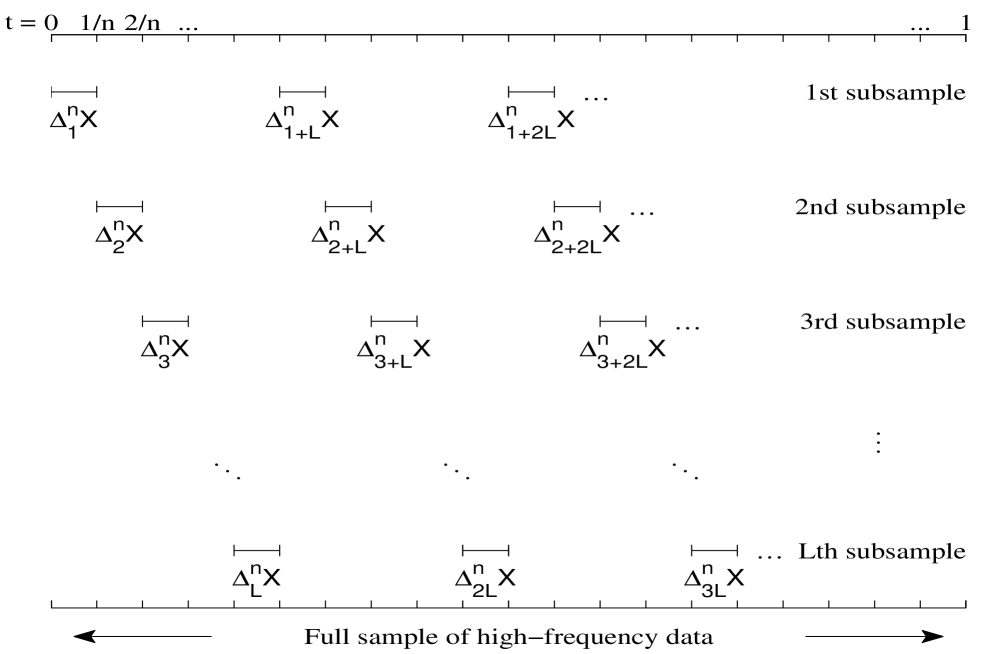

В предложенной методике заполнения пропусков используется понижающая дискретизация для учета вариаций мощности, что позволяет оптимизировать процесс и повысить эффективность системы.

Разработан устойчивый к шуму и скачкам оценочный метод асимптотической ковариационной матрицы биэнергетической вариации в высокочастотных финансовых данных.

Оценка асимптотической ковариационной матрицы, необходимой для построения доверительных интервалов в высокочастотном анализе финансовых данных, представляет собой сложную задачу, особенно в условиях рыночного шума. В статье ‘Inference from high-frequency data: A subsampling approach’ предложен новый метод оценки этой матрицы на основе субдискретизации, позволяющий получать согласованные оценки как в идеализированных, так и в зашумленных моделях. Суть подхода заключается в построении взвешенных копий статистики на основе локальных фрагментов данных и изучении вариации этих копий, что позволяет избежать необходимости в дополнительных оценках и гарантирует положительную полуопределенность полученной матрицы. Способен ли этот метод обеспечить надежную оценку погрешностей в высокочастотном анализе волатильности и расширить возможности статистического вывода в финансовых рынках?

Точность моделирования волатильности: Основы и вызовы

Точное моделирование процесса волатильности имеет первостепенное значение для финансового моделирования и управления рисками. Волатильность, отражающая степень изменчивости цен активов, напрямую влияет на оценку опционов, формирование портфелей и расчет показателей риска, таких как Value-at-Risk (VaR). Неверная оценка волатильности может привести к существенным ошибкам в ценообразовании деривативов и недооценке потенциальных убытков. Современные финансовые модели, такие как модель Блэка-Шоулза, в значительной степени полагаются на предположения о волатильности, и их точность напрямую зависит от адекватности этих предположений. Поэтому разработка и применение более точных методов моделирования волатильности, учитывающих особенности различных финансовых инструментов и рыночных условий, является ключевой задачей для профессионалов финансовой индустрии и исследователей.

Традиционные модели волатильности, базирующиеся на представлении логарифмической цены $\log(S_t)$ как итон-полумартингала, часто оказываются недостаточными для адекватного описания реальных финансовых рынков. Данный подход предполагает непрерывность ценового процесса и нормальное распределение изменений цены, что не всегда соответствует действительности, особенно в периоды высокой волатильности или резких скачков. Ограничения итон-полумартингальной модели проявляются при моделировании аномалий, таких как “толстые хвосты” распределения доходностей и кластеризация волатильности. Следовательно, для более точного прогнозирования и управления рисками требуется разработка альтернативных подходов, способных учитывать нелинейные зависимости и дискретные изменения цен, что стимулирует развитие более сложных моделей волатильности.

Определение характера колебаний цен — непрерывных или скачкообразных — представляет собой серьезную проблему в моделировании финансовых рынков. Традиционные подходы, предполагающие плавное изменение стоимости активов, могут давать неверные оценки рисков в периоды резких, неожиданных событий. Например, внезапные изменения в геополитической обстановке или публикации макроэкономической статистики способны вызвать скачки цен, которые не учитываются в моделях, основанных на непрерывных процессах. Неспособность адекватно отразить подобные “прыжки” в ценах приводит к недооценке волатильности и, как следствие, к неточным прогнозам и ошибочным инвестиционным решениям. Для повышения точности оценок необходимо разрабатывать модели, способные эффективно различать и учитывать как плавные колебания, так и резкие изменения стоимости активов, что требует применения более сложных математических инструментов и анализа данных.

Оценка плотности ядра стандартизованного <span class="katex-eq" data-katex-display="false">V^{\*} (q_k, r_k)^n</span> демонстрирует влияние параметров pp и LL. — Оценка плотности ядра стандартизованного $V^{\*} (q_k, r_k)^n$ демонстрирует влияние параметров pp и LL.

Оценка вариаций: От теории к практике

Квадратичная вариация $QV_T$ представляет собой теоретическую основу для оценки волатильности, определяя предел сумм квадратов приращений процесса на интервале [0, T] при стремлении длины подразделений к нулю. В практической реализации, применение квадратичной вариации требует осторожности, поскольку предполагает непрерывность процесса и игнорирует влияние микроструктурного шума, характерного для финансовых временных рядов. Несоблюдение этих условий может приводить к систематическим ошибкам в оценках волатильности. Таким образом, хотя квадратичная вариация предоставляет теоретически обоснованную меру общей вариации процесса, для получения надежных оценок на практике необходимы дополнительные методы коррекции и фильтрации данных.

Реализованная дисперсия ( $RV$ ) и силовая дисперсия ( $PV$ ) представляют собой практические оценки волатильности, используемые в финансовом анализе. $RV$ рассчитывается как сумма квадратов доходностей на высокочастотных данных и является простой в реализации оценкой. Однако, $PV$ превосходит $RV$ в условиях наличия скачков в ценах активов. Это связано с тем, что $PV$ использует взвешенные суммы доходностей, учитывающие порядок скачков, что позволяет более точно оценить вклад скачков в общую волатильность. В ситуациях, когда скачки незначительны или отсутствуют, $RV$ может быть достаточным, но при наличии выраженных скачков использование $PV$ является предпочтительным для получения более надежной оценки волатильности.

Высокочастотные финансовые данные, такие как тиковые цены или объемы торгов, неизбежно содержат $Microstructure N<a href="https://top-mob.com/chto-takoe-stabilizator-i-dlya-chego-on-nuzhen/">ois</a>e$ — шум, возникающий из-за дискретности рыночных котировок, негладкой природы ордербука и несовершенства механизмов формирования цен. Этот шум проявляется в виде случайных колебаний, не связанных с реальными изменениями стоимости базового актива, и может существенно искажать оценки волатильности. Для корректной оценки $Realized Variance$ и других показателей, основанных на высокочастотных данных, необходимо применять методы фильтрации и сглаживания, такие как использование весов, основанных на временных интервалах, или применение фильтров Винера, для уменьшения влияния $Microstructure Noise$ и получения более точных результатов.

Изменение параметра θ приводит к смещению распределения плотности вероятности <span class="katex-eq" data-katex-display="false"> V^{\*} (q_k, r_k)^n </span>, что демонстрирует влияние данного параметра на оценку плотности. — Изменение параметра θ приводит к смещению распределения плотности вероятности $V^{\*} (q_k, r_k)^n$ , что демонстрирует влияние данного параметра на оценку плотности.

Снижение шума и уточнение оценок

Предварительное усреднение (Pre-Averaging) является эффективным методом снижения шума микроструктуры в данных о ценах. Данный подход заключается в сглаживании высокочастотных данных путем вычисления среднего значения по нескольким последовательным наблюдениям. Это позволяет уменьшить влияние случайных колебаний, вызванных особенностями формирования котировок (например, асинхронными сделками или дискретностью времени). В результате, оценки волатильности становятся более устойчивыми и точными, особенно в условиях значительного шума микроструктуры, поскольку сглаживание уменьшает погрешность при расчете дисперсии ценовых изменений. Фактически, предварительное усреднение подготавливает данные для дальнейшего анализа и повышения надежности оценок волатильности.

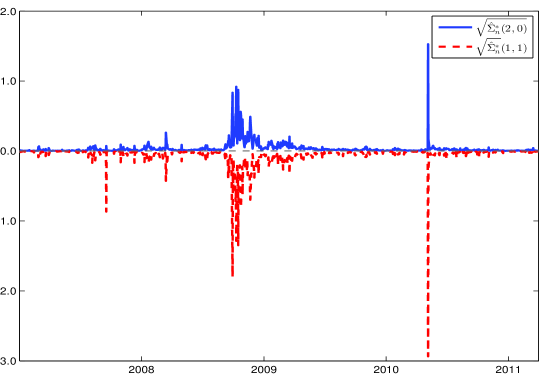
Метод вариации двух степеней (Bipower Variation) использует предварительное усреднение данных для оценки волатильности, особенно в условиях наличия скачков в ценовых рядах. В отличие от стандартных оценок волатильности, которые могут быть искажены скачками, вариация двух степеней позволяет получить более точные результаты, так как предварительное усреднение сглаживает высокочастотный шум и уменьшает влияние экстремальных значений. Этот подход обеспечивает значительное улучшение точности оценки волатильности в ситуациях, когда присутствуют резкие изменения цен, что делает его особенно полезным для анализа финансовых временных рядов.

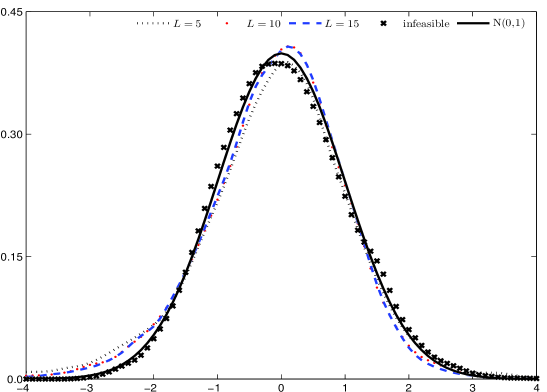
Разработанный оценочный метод подвыборки демонстрирует скорость сходимости $n^{-1/5}$ . Это означает, что ошибка оценки уменьшается пропорционально $n^{-1/5}$ , где n — размер выборки. Параметры метода, а именно количество подвыборок L и количество итераций p, растут со скоростью $O(n^{1/5})$ и $O(n^{1/10})$ соответственно. Такая асимптотическая сложность позволяет достичь оптимальной скорости сходимости при обработке больших объемов данных, сохраняя при этом вычислительную эффективность.

Сравнение подвыборки и асимптотической дисперсии показывает, что предложенный метод обеспечивает эффективное снижение дисперсии.

Оценка точности и надежности оценок

Асимптотическая дисперсия служит фундаментальным теоретическим ориентиром для оценки точности оценок волатильности. Она представляет собой предел дисперсии оценки при бесконечном размере выборки и позволяет определить, насколько близко оценка волатильности будет к истинному значению в идеальных условиях. Понимание асимптотической дисперсии критически важно, поскольку она определяет минимально достижимую точность любой оценки волатильности; любые оценки, приближающиеся к этой теоретической границе, считаются эффективными. $\sqrt{AVAR}$ фактически устанавливает стандартную ошибку оценки волатильности, что позволяет проводить статистические тесты и строить доверительные интервалы, необходимые для надежного анализа финансовых данных и управления рисками.

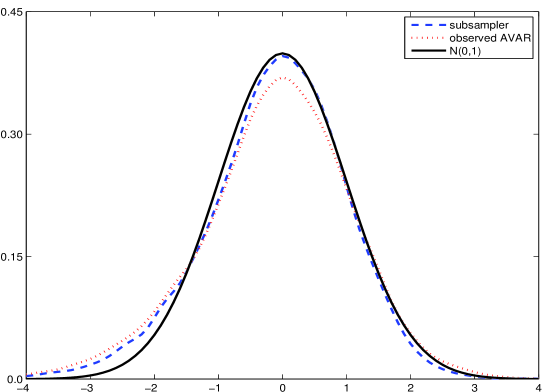
Для практической оценки точности оценок волатильности используются методы наблюдаемой асимптотической дисперсии (AVAR) и субдискретизации. Эти подходы позволяют количественно определить степень достоверности полученных результатов, предоставляя возможность сравнить различные оценки и выявить наиболее надежные. В основе этих методов лежит идея оценки асимптотической дисперсии, которая служит теоретическим ориентиром для оценки точности. Субдискретизация, в частности, предполагает повторную оценку волатильности на различных подвыборках данных, что позволяет сформировать представление о стабильности и надежности полученных результатов. Использование AVAR и субдискретизации способствует более обоснованному выбору оценок волатильности и повышению доверия к полученным выводам.

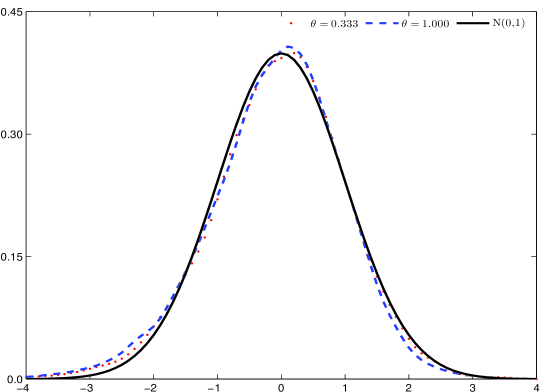
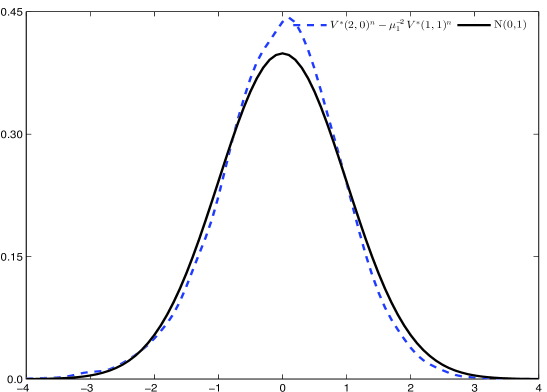
Разработанный метод подвыборки демонстрирует сходимость к асимптотической ковариационной матрице, что обеспечивает его состоятельность в оценке точности волатильности. В отличие от существующих аналогов, данный подход гарантирует положительную полуопределённость оценки, избегая проблем, связанных с нестабильностью и нереалистичными результатами. Подтверждением эффективности служит серия Монте-Карло симуляций, демонстрирующих превосходное соответствие полученных оценок стандартному нормальному распределению — это свидетельствует о высокой надежности и точности предложенного метода в практических приложениях оценки волатильности.

Временной ряд интегрированной дисперсии и стандартной ошибки позволяет оценить стабильность и точность оценки.

За пределами стандартных моделей: Учет скачков

Реальные финансовые рынки часто характеризуются внезапными, разрывными изменениями цен, которые не могут быть адекватно описаны стандартными моделями диффузии. Эти скачки, возникающие из-за неожиданных новостей, макроэкономических событий или изменений в настроениях инвесторов, приводят к нелинейностям в динамике цен и требуют использования более сложных инструментов. Модели диффузии с прыжками, известные как $Jump Diffusion Processes$ , позволяют учесть эти разрывные движения, добавляя к стандартному описанию процесса Винера случайные скачки. Эти модели представляют собой комбинацию непрерывного диффузионного компонента и дискретного процесса скачков, что позволяет более точно отражать реальное поведение цен на финансовых активах и улучшает точность прогнозирования волатильности и рисков.

Для повышения точности оценки волатильности на финансовых рынках, особенно в условиях резких скачков цен, применяются передовые методы, такие как вариация мощности. Этот подход позволяет более эффективно учитывать асимптотические свойства данных, что критически важно для выявления истинной волатильности, скрытой за случайными колебаниями. Традиционные методы оценки часто не способны адекватно отразить влияние этих скачков, приводя к искаженным результатам. Комбинируя вариацию мощности с глубоким анализом асимптотических свойств, исследователи добиваются более надежной и устойчивой оценки волатильности, что позволяет создавать более точные модели ценообразования и управления рисками. $\sigma^2$ — дисперсия, оцениваемая с использованием этих методов, позволяет лучше понимать динамику рынка и прогнозировать будущие колебания цен.

Перспективные исследования в области финансовой математики направлены на разработку адаптивных методов оценки волатильности, способных динамически реагировать на меняющиеся условия рынка. Вместо использования статических моделей, будущие алгоритмы будут стремиться к автоматической калибровке параметров оценки волатильности в режиме реального времени, учитывая как интенсивность, так и величину скачков цен. Такой подход позволит более точно отразить реальные рыночные процессы, особенно в периоды повышенной турбулентности и неопределенности. Особое внимание уделяется разработке методов, устойчивых к различным типам рыночного шума и способных эффективно различать истинные скачки цен от случайных флуктуаций. Успешная реализация этих исследований позволит значительно улучшить точность прогнозирования рисков и повысить эффективность управления инвестиционными портфелями.

Свойство стандартизованного выражения <span class="katex-eq" data-katex-display="false">V^{\\<i>}(2,0)^{n}-\mu\\_{1}^{-2}V^{\\</i>}(1,1)^{n}</span> остается неизменным. — Свойство стандартизованного выражения $V^{\\<i>}(2,0)^{n}-\mu\\_{1}^{-2}V^{\\</i>}(1,1)^{n}$ остается неизменным.

Предложенный в статье подход к оценке асимптотической ковариационной матрицы вариации биэнергии через подвыборку демонстрирует элегантность в своей простоте. Авторы, подобно архитекторам, стремящимся к устойчивости конструкции, акцентируют внимание на выявлении слабых мест в системе анализа данных. В частности, предложенный метод позволяет эффективно справляться с шумами микроструктуры и скачками, что критически важно для получения надежных оценок волатильности. Как отмечает Томас Кун: «Научные знания не растут поступательно, а формируются посредством революционных изменений в парадигмах». В данном исследовании, подвыборка выступает своего рода «революцией» в традиционных методах оценки, позволяя взглянуть на данные под новым углом и получить более точные результаты.

Куда Далее?

Предложенный подход к оценке асимптотической ковариационной матрицы вариации бистепеней, безусловно, вносит ясность в зашумлённый ландшафт высокочастотных данных. Однако, элегантность любой статистической конструкции раскрывается лишь в свете её ограничений. Очевидно, что предложенная подметодология, будучи устойчивой к микроструктурному шуму и скачкам, всё же предполагает стационарность базовых процессов. Вопрос о том, насколько эта предпосылка оправдана в реальности, остается открытым и требует дальнейшего исследования. Устойчивость системы не должна путать с всеядностью.

Более того, акцент на вариации бистепеней, хотя и полезен, не решает проблему выбора оптимальной частоты дискретизации. Поиск баланса между уменьшением шума и сохранением информации — вечная дилемма. Следующим шагом видится разработка адаптивных методов, способных динамически подстраиваться к меняющимся характеристикам данных, как живой организм приспосабливается к среде. Попытки упростить проблему, лишь смещают сложность в другое место.

В конечном счете, истинная проверка предложенного метода — это его применимость к реальным финансовым задачам, таким как оптимизация портфеля и управление рисками. Необходимо оценить, насколько точно и надёжно полученные оценки ковариационной матрицы позволяют улучшить практические результаты. Потому что, в конечном итоге, красота теории проявляется лишь в её способности объяснять и предсказывать мир вокруг.

Оригинал статьи: https://arxiv.org/pdf/2601.16668.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-26 13:05