Скрытые связи во временных рядах: новый подход к анализу данных

Автор: Денис Аветисян

Исследователи предлагают метод обнаружения неочевидных закономерностей в многомерных временных рядах без использования размеченных данных.

Сеть латентных связей, построенная на основе порогового значения косинусной близости 0.90, демонстрирует взаимосвязь между активами, где ребра указывают на сохраняющиеся отношения латентной близости.

Представлена схема построения сетей структурного подобия на основе скрытых представлений, позволяющая выявлять реляционные структуры в не стационарных данных временных рядов.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал

Анализ многомерных временных рядов часто затруднен нелинейностью и нестационарностью данных, что ограничивает возможности выявления скрытых взаимосвязей. В статье ‘Latent Structural Similarity Networks for Unsupervised Discovery in Multivariate Time Series’ предложен новый подход, основанный на построении сети структурного подобия в латентном пространстве, для неконтролируемого обнаружения взаимосвязей между сущностями во временных рядах. Метод позволяет агрегировать последовательные представления, полученные с помощью автоэнкодера на основе LSTM, в векторные вложения сущностей, а затем индуцировать разреженную сеть подобия, раскрывая потенциальные связи без предварительного определения целевой задачи. Возможно ли использовать данную структуру для построения более гибких и интерпретируемых моделей анализа данных в различных областях, от финансовых рынков до мониторинга сложных систем?

Раскрытие Скрытых Взаимосвязей в Комплексных Данных

Традиционные методы обнаружения взаимосвязей зачастую оказываются неэффективными при анализе многомерных временных рядов, упуская из виду тонкие, но критически важные связи. Сложность заключается в том, что данные, описывающие динамические системы — будь то финансовые рынки или сложные научные процессы — характеризуются высокой степенью шума и нелинейности. Стандартные алгоритмы, рассчитанные на поиск простых корреляций, не способны выявить скрытые зависимости, возникающие из-за временных задержек, нелинейных взаимодействий или влияния внешних факторов. В результате, важные сигналы могут быть погребены в шуме, а потенциально ценные закономерности остаются незамеченными, что ограничивает возможности прогнозирования и понимания исследуемых систем. Неспособность уловить эти нюансы приводит к неполной картине реальности и снижает эффективность аналитических моделей.

Современные финансовые и научные данные характеризуются огромным объемом и значительным уровнем шума, что создает серьезные трудности для выявления истинных взаимосвязей. Традиционные методы анализа зачастую оказываются неэффективными в таких условиях, поскольку не способны отделить полезный сигнал от случайных колебаний. Для преодоления этих проблем необходимы более сложные подходы, использующие алгоритмы машинного обучения и статистического моделирования, способные учитывать нелинейные зависимости и временные задержки. Разработка и применение таких методов позволяет извлекать ценную информацию из больших данных, открывая новые возможности для прогнозирования, оптимизации и принятия обоснованных решений в различных областях науки и экономики.

Существующие методы обнаружения взаимосвязей в данных часто опираются на заранее заданные метрики схожести, что существенно ограничивает их способность адаптироваться к тонким и сложным закономерностям. Такой подход предполагает, что исследователи заранее знают, какие характеристики данных являются релевантными для определения взаимосвязи, и фиксируют эти параметры в метрике. Однако, реальные данные, особенно в таких областях, как финансы или научные исследования, могут содержать скрытые или нелинейные зависимости, которые не учитываются жесткими критериями предопределенных метрик. В результате, значимые связи могут оставаться незамеченными, а анализ будет неполным или даже ошибочным. Разработка методов, способных самостоятельно выявлять релевантные признаки и адаптироваться к различным типам данных, является ключевой задачей для раскрытия полного потенциала информации, содержащейся в сложных наборах данных.

Матрица косинусной близости, вычисленная для агрегированных латентных представлений 20 криптовалют с часовым разрешением, демонстрирует степень их взаимосвязанности.

Представление Данных: Новый Взгляд на Обнаружение Взаимосвязей

Обучение представлений преобразует необработанные данные временных рядов в осмысленные векторные вложения, фиксирующие лежащие в их основе временные динамики. В отличие от прямого анализа исходных данных, обучение представлений позволяет выделить ключевые характеристики временного ряда, такие как тренды, сезонность и цикличность, кодируя их в компактном векторном пространстве. Это достигается путем применения алгоритмов, способных к снижению размерности и выявлению латентных факторов, влияющих на поведение временного ряда. В результате, каждое наблюдение во временном ряду представляется вектором, отражающим его положение и характеристики в этом пространстве, что существенно упрощает последующий анализ и выявление взаимосвязей.

Автокодировщики LSTM, реализованные по схеме «последовательность-к-последовательности», демонстрируют высокую эффективность в обучении векторных представлений временных рядов. Они используют рекуррентные слои LSTM для кодирования входной последовательности во внутреннее представление фиксированной длины, а затем декодируют это представление обратно в исходную последовательность. В процессе обучения автокодировщик стремится минимизировать ошибку реконструкции, что заставляет его сжимать входные данные, сохраняя при этом наиболее важные временные зависимости и паттерны. Это позволяет получить компактное и информативное представление данных, которое может быть использовано для последующего анализа и обнаружения взаимосвязей.

Полученные векторные представления, созданные методами обучения без учителя, значительно расширяют возможности выявления взаимосвязей в данных временных рядов. В отличие от анализа исходных данных, работа с компактными векторными эмбеддингами позволяет использовать более сложные и адаптивные алгоритмы обнаружения зависимостей, не ограничиваясь жесткими параметрами или предопределенными шаблонами. Это особенно важно при работе с нелинейными и динамически изменяющимися отношениями, где традиционные методы могут оказаться неэффективными. Более того, компактность векторных представлений снижает вычислительную сложность, позволяя обрабатывать большие объемы данных и проводить анализ в реальном времени.

Разреженные Графы Схожести: Точное Отображение Взаимосвязей

Разреженный граф схожести представляет собой способ моделирования взаимосвязей между объектами, где каждый объект выступает в роли узла, а отношения между ними — в роли ребер. Ключевой особенностью является ограничение количества ребер (разреженность), что существенно упрощает интерпретацию структуры графа и снижает вычислительные затраты при анализе и обработке данных. Такая структура позволяет выделить наиболее значимые связи, отфильтровывая менее важные, и делает граф более удобным для визуализации и анализа, особенно в контексте больших объемов данных, где полносвязный граф был бы чрезмерно сложным и неэффективным.

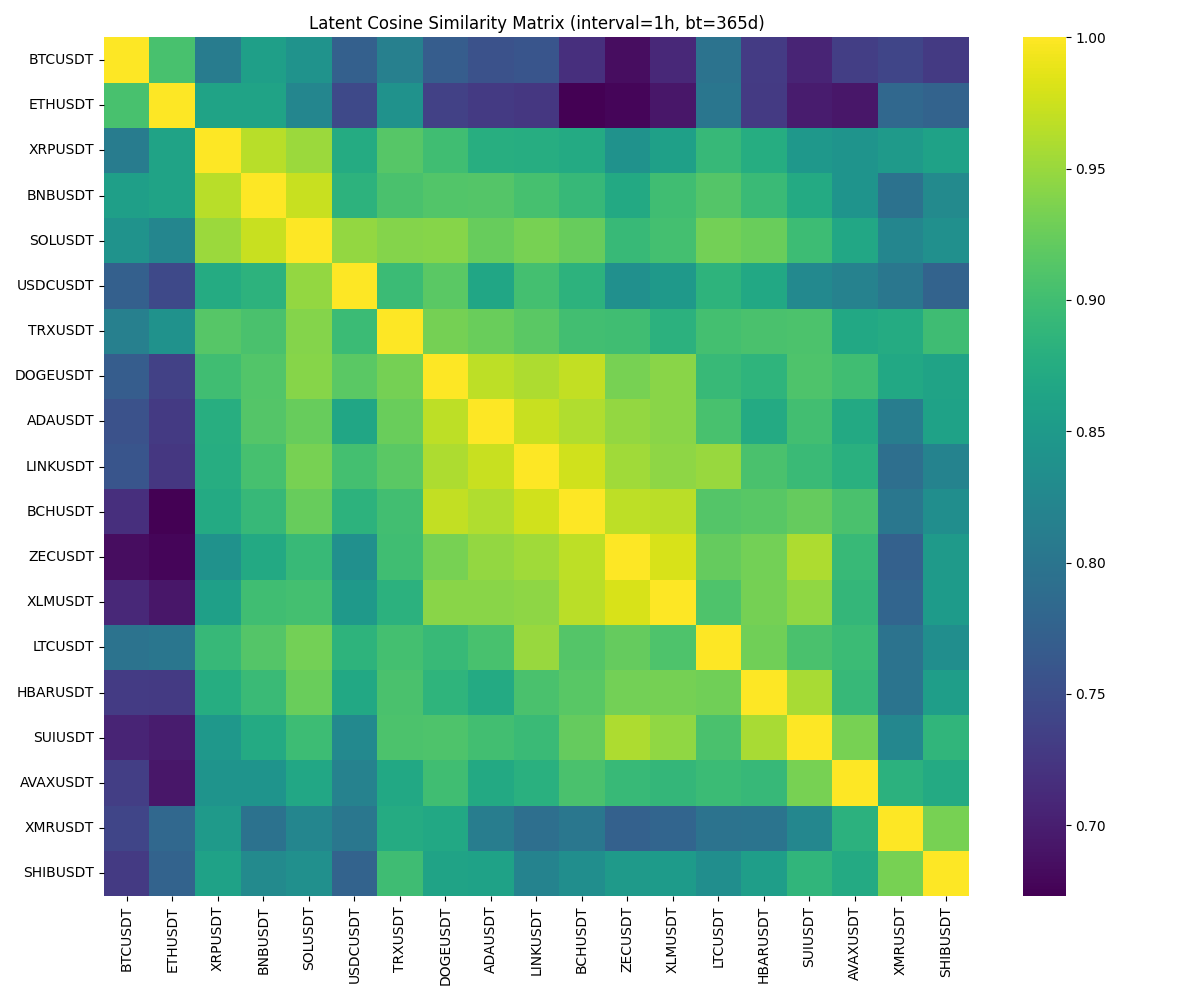
Построение графа основывается на количественной оценке сходства между векторными представлениями последовательностей (sequence embeddings). Для этого используются метрики, такие как косинусное сходство, которое вычисляет косинус угла между двумя векторами. Значение косинусного сходства варьируется от -1 до 1, где 1 указывает на полное сходство, 0 — на ортогональность (отсутствие сходства), а -1 — на полную противоположность. В контексте графов, более высокие значения косинусного сходства указывают на более тесную связь между соответствующими последовательностями, что определяет наличие и вес ребер между узлами.

В результате применения фиксированного порога схожести в 0.90, была сформирована разреженная сеть схожести, содержащая 64 ребра. Этот порог определил минимальный уровень схожести между векторами последовательностей, необходимый для установления связи между соответствующими узлами графа. Удержание только 64 ребер из потенциально большего числа связей обеспечивает разреженность графа, что упрощает его интерпретацию и снижает вычислительные затраты при анализе взаимосвязей между сущностями.

Подтверждение и Уточнение Взаимосвязей: Временная Стабильность и Коинтеграция

Временная стабильность играет ключевую роль в выявлении достоверных связей между активами. Анализ, учитывающий различные временные горизонты, позволяет определить, насколько устойчивы наблюдаемые корреляции и не являются ли они случайными флуктуациями. Если взаимосвязь между двумя активами сохраняется на протяжении значительных периодов времени, несмотря на изменения рыночных условий, это свидетельствует о более глубокой и надежной зависимости, чем просто краткосрочное совпадение. Отсутствие временной стабильности ставит под сомнение практическую ценность выявленной связи, поскольку она может быть ненадежной и непредсказуемой в будущем. Таким образом, оценка временной стабильности является необходимым шагом для подтверждения истинной взаимосвязи и использования её в стратегиях управления рисками или прогнозирования.

Применение тестов на коинтеграцию, в частности, теста Энгла-Грейнджера, к построенному разреженному графу схожести позволило подтвердить наличие долгосрочных равновесных взаимосвязей между активами. Данный подход выявил, что активы, представленные в графе как связанные, действительно склонны к совместному движению в долгосрочной перспективе, несмотря на краткосрочные колебания. Коинтеграция указывает на то, что существует линейная комбинация цен этих активов, которая является стационарным процессом, то есть не имеет тренда и возвращается к своему среднему значению. Это позволяет предположить, что отклонения от этой долгосрочной равновесной связи будут корректироваться со временем, что может быть использовано для разработки стратегий арбитража или хеджирования рисков. Фактически, подтверждение коинтеграции служит индикатором устойчивости выявленных связей между активами, повышая доверие к результатам анализа и возможности их практического применения.

Из 64 выявленных пар активов, анализ выявил, что 16 демонстрируют коинтеграцию на уровне доверия 0.95. Этот результат указывает на наличие устойчивых и статистически значимых долгосрочных равновесных взаимосвязей между данными активами. Коинтеграция предполагает, что несмотря на краткосрочные колебания, цены этих активов имеют тенденцию двигаться вместе в долгосрочной перспективе, что может быть использовано для разработки эффективных стратегий торговли и управления рисками. Высокий уровень доверия подтверждает надежность этих взаимосвязей и их потенциальную ценность для инвесторов и финансовых аналитиков.

Представленная работа демонстрирует элегантность подхода к анализу многомерных временных рядов, фокусируясь на выявлении скрытых структурных связей. Авторы, подобно искусным архитекторам, стремятся к простоте и ясности в построении модели, что особенно ценно при работе с не стационарными данными. В этой связи вспоминается высказывание Андрея Николаевича Колмогорова: «Математика — это искусство открывать закономерности в хаосе». Подобно тому, как математик ищет порядок в кажущемся хаосе, данное исследование выявляет взаимосвязи в сложном потоке временных данных, используя latent representation и similarity network для раскрытия скрытых закономерностей и обеспечения гибкого подхода к exploratory analysis.

Куда Ведут Эти Пути?

Представленный подход, стремясь к обнаружению скрытых связей в многомерных временных рядах, неизбежно сталкивается с вечными компромиссами. Элегантность упрощения модели всегда оплачивается потерей детализации, а стремление к изощрённости — риском переобучения и потери обобщающей способности. Очевидно, что устойчивость к не стационарности, хоть и заявленная, требует более глубокого изучения в контексте данных с выраженной долгосрочной трендовостью или сезонностью. Необходимо учитывать, что простое обнаружение связей — это лишь первый шаг; интерпретация этих связей, придание им осмысленного контекста, остаётся сложной задачей.

Будущие исследования, вероятно, будут направлены на интеграцию механизмов внимания, позволяющих модели фокусироваться на наиболее значимых временных интервалах и взаимосвязях. Перспективным направлением представляется адаптация подхода к работе с неполными данными, учитывая, что в реальных приложениях пропуски являются скорее правилом, чем исключением. Не стоит забывать и о необходимости разработки более эффективных метрик оценки качества обнаруженных структур, выходящих за рамки простых корреляций.

В конечном счёте, ценность предложенного подхода заключается не столько в абсолютной точности обнаружения связей, сколько в предоставлении исследователю гибкого инструмента для предварительного анализа и генерации гипотез. Как и любая система, она лишь отражение тех принципов, которые в неё заложены, и её эффективность напрямую зависит от способности исследователя правильно интерпретировать полученные результаты.

Оригинал статьи: https://arxiv.org/pdf/2601.18803.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-28 12:20