Скрытые структуры графов: как выявить закономерности в шуме

Автор: Денис Аветисян

Новый подход позволяет обнаруживать и визуализировать высокоуровневые структуры в графах, анализируя закономерности в переупорядоченных матрицах смежности.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал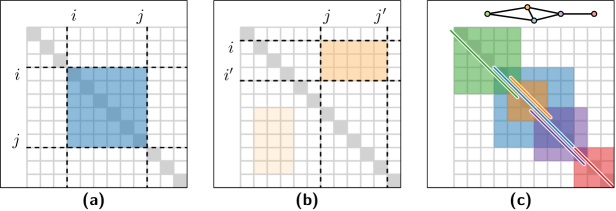

На основе анализа структуры шума, разработанный конвейер выявления закономерностей определяет и пересчитывает как клики, так и биклики, после чего осуществляет выборку клик для повышения точности обнаружения.

В статье представлен метод выявления ‘зашумленных’ графовых паттернов и их представление с помощью упрощенной мотивной техники, названной ‘Кольцевые Мотивы’.

Выявление значимых структур в графах затруднено как вычислительной сложностью поиска известных паттернов, так и наличием шума в реальных данных. В данной работе, ‘Noisy Graph Patterns via Ordered Matrices’, предложен новый подход к обнаружению и визуализации таких структур, основанный на оптимальной перестановке матрицы смежности с использованием статистики $I$ Морана. Предложенный метод позволяет определить допустимый уровень шума для стандартных графовых паттернов (клики, биклики, звезды) и эффективно декомпозировать матрицу на «зашумленные» подпаттерны. Возможно ли с помощью данного подхода разработать новые методы анализа и визуализации графов, позволяющие более эффективно извлекать полезную информацию из сложных сетевых данных?

Разоблачение Скрытых Структур: Пределы Традиционного Анализа Графов

Традиционный анализ графов часто сосредотачивается на выявлении полных подграфов, известных как клики, где каждая вершина связана со всеми остальными. Однако, в реальных сетях, будь то социальные взаимодействия, биологические системы или технологические инфраструктуры, подобные идеально связанные структуры встречаются крайне редко. Эти сети по своей природе зашумлены — связи могут отсутствовать, быть неполными или отражать лишь частичную информацию. Вследствие этого, строгое требование полной связности в определении клик приводит к упущению значительных, но неидеальных, паттернов, которые несут важную информацию об организации сети. Игнорирование этих неполных структур ограничивает возможности понимания сложных взаимосвязей и выявления скрытых закономерностей в реальных данных.

Традиционные методы анализа графов, ориентированные на поиск полных подграфов, таких как клики, часто упускают из виду важные, но неидеальные, паттерны, присутствующие в реальных сетях. Эти неполные структуры, хотя и не соответствуют строгим математическим определениям, несут в себе ценную информацию об организации сети и взаимосвязях между её элементами. Игнорирование этих «зашумленных» паттернов приводит к упрощенному пониманию сложных систем, поскольку они могут отражать важные функциональные группы, иерархии или динамические процессы, которые не проявляются в полных подграфах. Таким образом, способность выявлять и интерпретировать эти несовершенные структуры является ключевым шагом к более полному и точному анализу сетевых данных.

Для выявления неполных, зашумленных паттернов в сетевых структурах необходимы инновационные методы, способные отделять полезный сигнал от случайного шума. Традиционные алгоритмы, ориентированные на поиск совершенных структур, часто оказываются неэффективными в реальных сетях, где данные редко бывают идеальными. Новые подходы, такие как вероятностные модели и алгоритмы машинного обучения, позволяют учитывать неточности и неполноту данных, выявляя скрытые связи и закономерности, которые иначе остались бы незамеченными. Эти методы не просто ищут точные совпадения, а оценивают вероятность существования связи, даже если она не выражена полностью, что значительно повышает точность анализа и позволяет раскрыть более полную картину организации сети.

Для начала анализа сетевых структур ключевым шагом является представление связей между элементами в виде матрицы смежности. Эта матрица, где каждая строка и столбец соответствуют отдельному элементу сети, а пересечение — наличию или отсутствию связи между ними, служит основой для выявления закономерностей. $A_{ij} = 1$ указывает на наличие соединения между элементами $i$ и $j$ , в то время как $A_{ij} = 0$ означает его отсутствие. Использование матрицы смежности позволяет математически формализовать структуру сети и применять алгоритмы для обнаружения скрытых кластеров, паттернов и связей, которые невозможно увидеть при простом визуальном анализе. Она представляет собой компактный и эффективный способ кодирования сетевой информации, необходимый для последующего применения методов анализа графов и машинного обучения.

Переупорядочение матрицы данных FLT позволяет выявить более четкие паттерны при <span class="katex-eq" data-katex-display="false">\sigma = 0.3</span> и <span class="katex-eq" data-katex-display="false">\tau = 1.0</span>, в отличие от исходной матрицы, где паттерны менее выражены и шумны при <span class="katex-eq" data-katex-display="false">\sigma = 0.2</span> и <span class="katex-eq" data-katex-display="false">\tau = 0.6</span>. — Переупорядочение матрицы данных FLT позволяет выявить более четкие паттерны при $\sigma = 0.3$ и $\tau = 1.0$ , в отличие от исходной матрицы, где паттерны менее выражены и шумны при $\sigma = 0.2$ и $\tau = 0.6$ .

За Пределами Совершенства: Перечисление и Отбор Устойчивых Паттернов

Процесс выявления структурных паттернов в графе начинается с систематического перебора возможных комбинаций узлов в матрице смежности. В отличие от традиционных методов, ориентированных исключительно на поиск совершенных клик и биклик, наша методология расширяет область поиска, учитывая и неполные, приближенные структуры. Это достигается путем анализа всех подграфов определенного размера, что позволяет обнаружить паттерны, которые могут содержать незначительные отклонения от идеальной формы, но при этом отражают значимые взаимосвязи между узлами. Перебор осуществляется алгоритмически, обеспечивая полноту охвата потенциальных структур.

Метод отбора паттернов осуществляет приоритизацию наиболее репрезентативных и непересекающихся структур, полученных в результате первоначальной перечислительной процедуры. Данный процесс включает оценку каждого паттерна по критериям, отражающим его значимость и уникальность в контексте графа. Непересекающиеся паттерны выбираются для максимизации информационной насыщенности и предотвращения избыточности в конечном наборе отобранных структур. Приоритизация осуществляется с использованием метрик, позволяющих ранжировать паттерны по степени их соответствия заданным критериям значимости, что обеспечивает выделение наиболее важных и информативных структур в графе.

Предлагаемый подход к выявлению паттернов в графах обладает устойчивостью к неполноте и ошибкам в данных. В отличие от методов, требующих строгого соответствия идеальным структурам, данная методика позволяет идентифицировать паттерны, содержащие незначительные отклонения от ожидаемой конфигурации. Это достигается за счет учета вариаций в связях и узлах, что позволяет обнаруживать структуры, которые могли бы быть пропущены при использовании более строгих критериев. Способность учитывать “зашумленные” паттерны существенно повышает надежность анализа, особенно в реальных сетях, где данные часто содержат неточности или неполную информацию.

Применение подхода, ориентированного на максимальные непересекающиеся (disjoint) паттерны, обеспечивает выявление наиболее отличных и информативных структур внутри сети. Максимальность паттерна подразумевает, что к нему нельзя добавить ни одного узла или ребра без нарушения его определения. Непересекаемость гарантирует, что каждый узел и каждое ребро учитываются только в одном паттерне, избегая избыточности и обеспечивая более четкое представление об организации сети. В результате, данный метод позволяет идентифицировать ключевые, независимые компоненты сетевой структуры, игнорируя менее значимые или дублирующие элементы, что повышает точность анализа и интерпретации данных.

Анализ матрицы 58 из набора данных FLT показал, что увеличение параметров σ и τ приводит к снижению шума в паттернах, уменьшению числа обнаруженных границ и усложнению кольцевых мотивов.

Визуализация Несовершенства: Кодирование Шума в Упрощении Кольцевых Мотивов

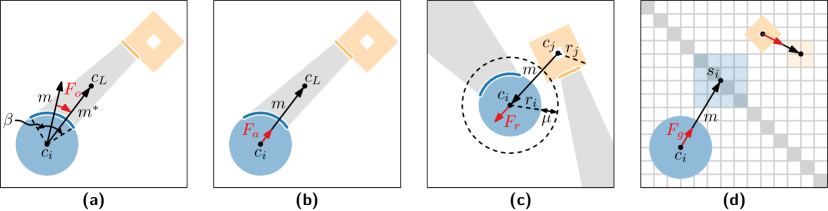
Метод упрощения кольцевых мотивов (Ring Motif Simplification) представляет собой визуализацию идентифицированных паттернов в графах. Этот подход позволяет отображать обнаруженные подграфы в виде графических элементов — мотивов, где каждый мотив представляет собой определенную структуру узлов и связей. Визуализация строится таким образом, чтобы форма и расположение мотивов отражали их характеристики и взаимосвязи в исходном графе, облегчая анализ и выявление значимых структурных элементов. Данная техника предназначена для работы с графами различной сложности и масштаба, обеспечивая возможность изучения и сравнения большого количества паттернов.

Метод упрощения кольцевых мотивов (Ring Motif Simplification) не ограничивается выявлением только идеальных паттернов. Ключевым аспектом является кодирование уровня шума непосредственно в глифах, представляющих эти паттерны. Уровень шума, связанный с конкретным паттерном, визуализируется через изменения в форме или цвете глифа, позволяя пользователю оценить степень неточности или вариативности обнаруженного мотива. Таким образом, метод предоставляет информацию не только о присутствии паттерна, но и о его надежности и распространенности в сети, что критически важно для анализа сложных и зашумленных данных.

Для визуализации упрощенных кольцевых мотивов используется алгоритм форсированного направленного размещения (force-directed layout). Этот алгоритм позволяет расположить глифы, представляющие выявленные паттерны, таким образом, чтобы отразить структуру сети и взаимосвязи между ними. Реализация обеспечивает производительность свыше 1000 итераций в секунду, что позволяет эффективно обрабатывать большие объемы данных и оперативно визуализировать сложные сетевые структуры. Высокая скорость итераций способствует быстрому определению кластеров и выявлению как сильных, так и слабых связей между различными паттернами в сети.

Данный подход позволяет исследовать сложные сети, визуализируя не только сильные, но и слабые связи между элементами. Особое внимание уделяется выявлению распространенности неполных или несовершенных паттернов, которые часто встречаются в реальных данных. Визуализация не ограничивается представлением только четко определенных структур, а кодирует информацию о степени несоответствия паттерна, позволяя оценить надежность и распространенность как сильных, так и слабых связей в сети и, таким образом, получить более полное представление о ее структуре и особенностях.

Система компоновки на основе сил использует вращательное воздействие, притяжение связей, отталкивание глифов и гравитационное воздействие шаблона для организации элементов.

От Мозга к Социальным Сетям: Подтверждение Эффективности Подхода

Применение разработанного метода к набору данных FLT, представляющему собой карту функциональной связности мозга, позволило выявить ранее скрытые паттерны нейронной коммуникации. Анализ данных FLT продемонстрировал возможность обнаружения специфических кластеров областей мозга, активно взаимодействующих друг с другом во время выполнения различных когнитивных задач. Эти паттерны, невидимые при использовании традиционных методов анализа, указывают на существование ранее неизвестных функциональных связей и могут быть ключевыми для понимания механизмов работы мозга и развития нейродегенеративных заболеваний. Выявленные структуры нейронной коммуникации представляют собой перспективную область для дальнейших исследований в области нейронаук и могут способствовать разработке новых методов диагностики и лечения заболеваний головного мозга.

Анализ данных о социальной сети членов клуба карате, известной как ZKC, позволил выявить ключевые подгруппы и их внутреннюю структуру. Исследование продемонстрировало способность метода к автоматическому определению наиболее влиятельных и сплоченных групп внутри сети, основываясь исключительно на паттернах взаимодействия. В результате, стало возможным визуализировать и понять организацию клуба, обнаружив не только отдельные фракции, но и связи между ними, что может быть полезно для анализа динамики коллектива и выявления лидеров мнений. Данный подход позволяет количественно оценить степень сплоченности каждой подгруппы и их роль в общей структуре социальной сети, предоставляя ценные сведения о социальных процессах, происходящих внутри коллектива.

Анализ набора данных SCH, отражающего социальные взаимодействия в начальной школе, выявил закономерности, связанные с формированием дружеских связей и проявлениями социальной изоляции. Исследование позволило идентифицировать группы детей, объединенных общими интересами и симпатиями, а также выявить отдельных учеников, испытывающих трудности в установлении социальных контактов. Полученные результаты демонстрируют, что предложенный подход способен не только описывать структуру социальных сетей, но и выявлять тонкие нюансы, определяющие социальную динамику в детском коллективе, что может быть полезно для педагогов и психологов, работающих с детьми.

Разработанный алгоритм, включающий перечисление и отбор паттернов, демонстрирует впечатляющую масштабируемость. Полный цикл обработки, от анализа исходных данных до выявления ключевых структур, выполняется менее чем за одну секунду на современном ноутбуке. Эта высокая скорость позволяет применять данный подход к анализу больших и сложных сетевых данных, открывая возможности для изучения разнообразных систем — от нейронных связей в мозге до социальных взаимодействий в коллективах. Быстродействие алгоритма делает его практичным инструментом для исследователей, работающих с большими объемами данных и нуждающихся в оперативной обработке и анализе сетевых структур.

Успешное применение разработанного подхода к анализу совершенно различных наборов данных — от карт функциональной связности мозга (FLT) до социальных сетей карате (ZKC) и взаимодействий в начальной школе (SCH) — наглядно демонстрирует его универсальность и практическую ценность. Этот метод позволяет выявлять скрытые структуры в сетях, независимо от их природы, что открывает новые возможности для исследования сложных систем. Подтвержденная способность обнаруживать закономерности в столь разнообразных контекстах указывает на то, что предложенный подход является мощным инструментом для анализа взаимосвязей и выявления ключевых элементов в любых сложных сетях, будь то нейронные связи или социальные взаимодействия.

Матрица 35 набора данных FLT при <span class="katex-eq" data-katex-display="false">\sigma = 0.5</span> и <span class="katex-eq" data-katex-display="false">\tau = 0.9</span> демонстрирует характерное распределение значений. — Матрица 35 набора данных FLT при $\sigma = 0.5$ и $\tau = 0.9$ демонстрирует характерное распределение значений.

Оптимизация Обнаружения Паттернов: Повышение Эффективности Переупорядочением Матрицы

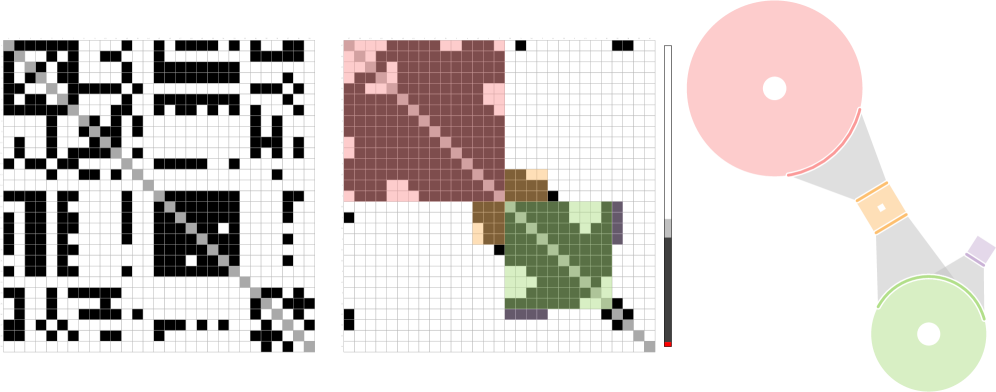
Для повышения эффективности анализа сложных сетей применяется переупорядочение матрицы смежности, основанное на статистическом показателе Морана I. Этот метод позволяет расположить связанные узлы ближе друг к другу в матрице, что значительно упрощает выявление закономерностей и снижает вычислительную сложность. Суть подхода заключается в минимизации расстояния между взаимодействующими элементами, что способствует более быстрому и точному определению кластеров и общих структурных особенностей сети. Такое предварительное преобразование матрицы смежности позволяет существенно оптимизировать дальнейший процесс поиска и отбора паттернов, особенно в случае больших и сложных сетевых систем.

Для облегчения обнаружения закономерностей в сложных сетях применяется оптимизированный процесс, использующий решатель Concorde TSP, доступный через сервер NEOS. Этот алгоритм, изначально предназначенный для решения задачи коммивояжера, эффективно переупорядочивает элементы матрицы смежности, располагая связанные узлы ближе друг к другу. Такое преобразование значительно снижает вычислительную сложность последующего анализа, позволяя более быстро и точно идентифицировать значимые паттерны и связи в больших сетевых структурах. Благодаря этому подходу, сложные задачи поиска закономерностей становятся более управляемыми и доступными для исследования даже в очень крупных и сложных системах.

Переупорядочение матрицы смежности, критически важное для повышения эффективности обнаружения паттернов, выполняется примерно за 20 секунд при обработке экземпляров SCH с использованием сервера NEOS. Этот временной показатель демонстрирует высокую скорость алгоритма и его применимость к задачам, требующим оперативной обработки больших объемов данных. Использование сервера NEOS, предоставляющего доступ к Concorde TSP Solver, позволяет эффективно решать задачу оптимизации порядка расположения узлов матрицы, что существенно сокращает время вычислений и обеспечивает возможность анализа сложных сетевых структур в разумные сроки. Такая скорость обработки открывает перспективы для исследования масштабных сетей и выявления скрытых взаимосвязей в различных областях науки и техники.

Предварительная обработка матрицы, заключающаяся в ее реорганизации, позволяет существенно снизить вычислительную сложность при поиске и отборе паттернов. Такой подход базируется на уменьшении количества операций, необходимых для анализа связей между узлами сети. Вместо перебора всех возможных комбинаций, реорганизованная матрица позволяет сосредоточиться на наиболее значимых областях, где вероятны интересные паттерны. Это приводит к значительному ускорению процесса, позволяя эффективно анализировать даже очень большие и сложные сетевые структуры, и выявлять скрытые взаимосвязи, которые могли бы остаться незамеченными при использовании стандартных методов.

Разработанный подход открывает новые возможности для исследования масштабных сетевых структур и выявления скрытых взаимосвязей в сложных системах. Оптимизация обработки матриц позволяет эффективно анализировать данные, ранее недоступные для детального изучения из-за вычислительных ограничений. Данная методика не только ускоряет процесс обнаружения закономерностей, но и способствует более глубокому пониманию организации и функционирования сложных взаимодействующих элементов, что особенно важно в таких областях, как биоинформатика, социальные науки и анализ транспортных сетей. Возможность быстрого и точного анализа больших объемов данных открывает перспективы для прогнозирования, моделирования и принятия обоснованных решений в самых разных сферах человеческой деятельности.

Представленное исследование демонстрирует стремление к упрощению сложных структур, что находит отклик в словах Давида Гильберта: «Вся математика сводится к разрешению уравнений». Работа акцентирует внимание на выявлении паттернов в зашумленных графах посредством переупорядочивания матриц смежности. Этот подход к разложению графов на базовые элементы, а именно, на кольцевые мотивы (Ring Motifs), позволяет выделить существенные связи и отбросить несущественные детали. Как и в математике, где поиск решений уравнений требует концентрации на главном, данное исследование стремится к ясности и лаконичности в представлении сложных данных, что способствует более глубокому пониманию структуры графов.

Куда Далее?

Представленный подход, стремясь выявить структуры в зашумленных графах через переупорядочивание матриц смежности, неизбежно сталкивается с вопросом о границах упрощения. Вместо бесконечного поиска «идеального» Ring Motif, представляется более плодотворным признать присущую графам неоднозначность. Стремление к избыточному детализированию лишь маскирует фундаментальную сложность, а не раскрывает её. Реальная ценность заключается не в количестве выявленных мотивов, а в осознании того, что их количество принципиально не ограничено.

Будущие исследования, вероятно, должны сместиться от алгоритмической гонки за точностью к разработке метрик, оценивающих значимость упрощения. Необходимо понимать, какая информация теряется при переходе от исходного графа к его Ring Motif-представлению, и как эта потеря влияет на интерпретацию. Иначе, мы рискуем создать инструмент, который лишь подтверждает наши собственные предубеждения, а не раскрывает истинную природу данных.

Очевидно, что представленный метод — лишь один из возможных путей. Более фундаментальный вопрос заключается в том, насколько вообще возможно объективно «увидеть» структуру в зашумленных данных. Возможно, истинная красота графов заключается не в их упорядоченности, а в их хаосе. И в этом хаосе — своя, непостижимая гармония.

Оригинал статьи: https://arxiv.org/pdf/2601.11171.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-20 13:06