Разумные сети: Новый подход к стабильности и интерпретируемости

Автор: Денис Аветисян

В статье представлена инновационная архитектура глубокого обучения, сочетающая рациональные блоки и декомпозицию дисперсионного анализа для повышения надежности и понимания работы нейронных сетей.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Телеграм канал

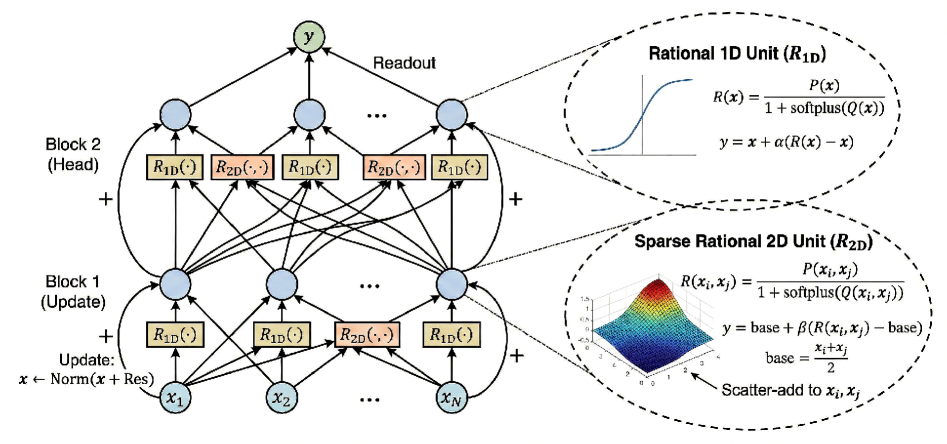
Архитектура глубокой рациональной ANOVA-сети (RAN) использует глубокий «скелет» из последовательно соединенных остаточных блоков, каждый из которых выполняет разреженную попарную передачу сообщений и обновление узлов, а также обучаемые рациональные единицы <span class="katex-eq" data-katex-display="false">R_1^{DR_{1D}}</span> и <span class="katex-eq" data-katex-display="false">R_2^{DR_{2D}}</span> с инициализацией идентичности посредством остаточного гейтинга <span class="katex-eq" data-katex-display="false">y = x + \alpha(R(x) - x)</span>, при этом знаменатели, обеспечивающие стабильность и отсутствие полюсов, формируются с использованием функции <span class="katex-eq" data-katex-display="false">1 + \text{softplus}(\cdot)</span>. — Архитектура глубокой рациональной ANOVA-сети (RAN) использует глубокий «скелет» из последовательно соединенных остаточных блоков, каждый из которых выполняет разреженную попарную передачу сообщений и обновление узлов, а также обучаемые рациональные единицы $R_1^{DR_{1D}}$ и $R_2^{DR_{2D}}$ с инициализацией идентичности посредством остаточного гейтинга $y = x + \alpha(R(x) - x)$ , при этом знаменатели, обеспечивающие стабильность и отсутствие полюсов, формируются с использованием функции $1 + \text{softplus}(\cdot)$ .

Предлагается архитектура Rational-ANOVA Networks (RAN), объединяющая рациональные функции и ANOVA-декомпозицию для стабильного обучения, интерпретируемости и эффективного решения задач символьной регрессии.

Ограниченность традиционных нейронных сетей в интерпретируемости и контроле над функциональным классом препятствует эффективному моделированию сложных зависимостей. В данной работе представлена архитектура ‘Rational ANOVA Networks’ (RAN), основанная на разложении по функциональному дисперсионному анализу (ANOVA) и рациональной аппроксимации Паде. RAN моделирует функцию как композицию основных эффектов и разреженных парных взаимодействий, параметризованных стабильными рациональными единицами, обеспечивающими устойчивость обучения и улучшенную экстраполяцию. Способна ли данная структура, сочетающая в себе преимущества ANOVA и рациональных сетей, обеспечить новый уровень контроля и интерпретируемости в глубоком обучении?

Пределы Современных Глубоких Нейронных Сетей

Традиционные архитектуры глубокого обучения, такие как многослойные перцептроны (MLP), часто демонстрируют ограниченные возможности в задаче аппроксимации функций и могут быть подвержены нестабильности в процессе обучения. Эта проблема связана с тем, что MLP полагаются на последовательное применение линейных преобразований и нелинейных активаций, что затрудняет эффективное моделирование сложных взаимосвязей. Неправильная инициализация весов или недостаточная регуляризация могут приводить к затуханию или взрыву градиентов, что препятствует сходимости алгоритма. В результате, обучение глубоких сетей требует значительных вычислительных ресурсов и тщательной настройки гиперпараметров, а достижение устойчивой производительности остается сложной задачей, особенно при работе с высокоразмерными данными или нелинейными функциями.

Достижение устойчивой производительности в современных нейронных сетях часто требует кропотливой настройки начальных параметров и применения методов регуляризации. Однако, несмотря на их широкое использование, эти подходы зачастую носят эмпирический характер и лишены строгих теоретических обоснований. Выбор конкретных значений для инициализации весов или параметров регуляризации, как правило, осуществляется методом проб и ошибок, что затрудняет воспроизводимость результатов и перенос моделей на новые задачи. Отсутствие гарантий сходимости и оптимальности этих процедур подчеркивает необходимость разработки более надежных и предсказуемых алгоритмов обучения, способных обеспечить стабильную и эффективную работу нейронных сетей в различных условиях.

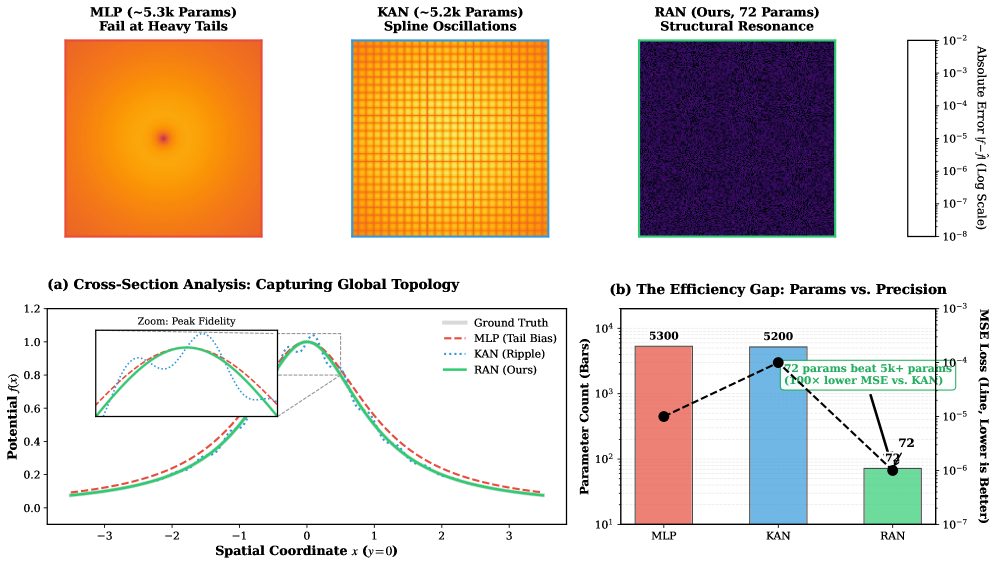
Стандартные методы аппроксимации, такие как многослойные персептроны (MLP), испытывают трудности при работе с функциями, содержащими резкие переходы и “тяжелые хвосты” — особенности, которые значительно усложняют процесс обучения и снижают точность предсказаний. Это связано с ограниченной выразительностью используемых представлений данных. Новая архитектура RAN, разработанная для решения данной проблемы, демонстрирует значительно более высокую точность при аппроксимации функций с резкими особенностями по сравнению с традиционными MLP и KANs. Результаты показывают, что RAN эффективно захватывает и моделирует сложные зависимости, обеспечивая более надежные и точные прогнозы в случаях, когда стандартные методы терпят неудачу, что подчеркивает необходимость разработки более выразительных моделей для решения сложных задач машинного обучения.

В отличие от моделей MLP, склонных к смещению в хвосте распределения, и KAN, демонстрирующих колебания, модель RAN достигает аналитической точности в определении структурного резонанса, превосходя базовые модели в два порядка величины при использовании менее 1,5% их параметров.

Рациональные Единицы: Основа Стабильного Обучения

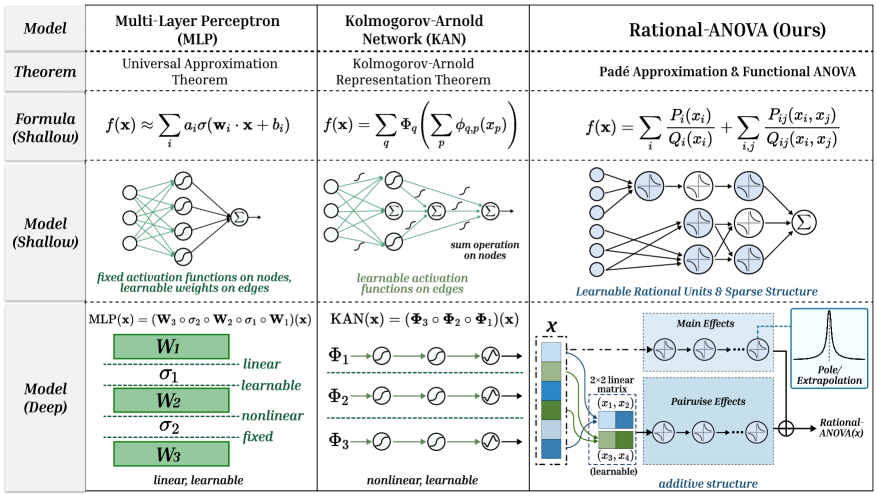
Рациональные единицы (Rational Units, RAN) представляют собой мощный и выразительный нелинейный слой для глубоких нейронных сетей, основанный на концепции аппроксимации Паде. В отличие от традиционных нелинейностей, таких как ReLU или sigmoid, RAN использует отношение двух полиномов для представления функции активации. Это позволяет моделировать более сложные зависимости в данных и обеспечивает повышенную гибкость в обучении. Аппроксимация Паде позволяет приблизить широкую гамму функций, что делает RAN применимым в различных задачах машинного обучения, требующих высокой выразительности нелинейного слоя. Использование полиномиального представления также способствует улучшению свойств оптимизации и стабильности обучения модели.

В архитектуре RAN функции представляются в виде отношений полиномов, что обеспечивает повышенную гибкость по сравнению с традиционными подходами. Это представление позволяет избежать проблем затухающих или взрывающихся градиентов, часто возникающих в глубоких нейронных сетях. Теоретически доказано, что спектральная норма Якобиана ограничена величиной $exp(Lϵ(Kϕ-1))$ , что подтверждает стабильный поток градиентов во время обучения. Ограничение спектральной нормы гарантирует, что градиенты не становятся слишком большими или слишком маленькими, способствуя более эффективной и надежной оптимизации модели.

Ограничение положительного знаменателя является критически важным для обеспечения численной устойчивости и предотвращения возникновения сингулярностей в процессе обучения. В архитектуре Rational Units (RAN) этот механизм гарантирует, что знаменатель рациональной функции всегда остается положительным. Это предотвращает неопределенности и резких изменений в выходных данных, которые могут привести к взрыву или исчезновению градиентов. Практически, это достигается путем применения соответствующих регуляризаций или ограничений к параметрам модели, формирующим знаменатель. Без этого ограничения, небольшие изменения во входных данных или параметрах могут вызвать значительные колебания в выходных значениях, делая обучение нестабильным и приводя к непредсказуемым результатам. Таким образом, положительный знаменатель выступает в качестве ключевого элемента, обеспечивающего надежность и предсказуемость процесса обучения моделей RAN.

Модель RAN демонстрирует оптимальный баланс между точностью восстановления изображения (PSNR) и количеством параметров, занимая лидирующие позиции на Парето-фронте при обработке данных PolyU.

Аддитивное Разложение ANOVA: Создание Контролируемых Сетей

В архитектуре RAN используется аддитивное разложение по критерию ANOVA для представления сложных функций в виде суммы главных эффектов и разреженных парных взаимодействий. Это означает, что каждая выходная переменная модели представляется как сумма вкладов от отдельных входных признаков (главные эффекты) и комбинаций пар признаков (взаимодействия). Разреженность взаимодействий подразумевает, что рассматривается лишь небольшая часть всех возможных пар признаков, что снижает вычислительную сложность и улучшает обобщающую способность модели. Математически, функция может быть выражена как $f(x) = \sum_{i} x_i + \sum_{i,j} x_i x_j$ , где первый член представляет главные эффекты, а второй — разреженные парные взаимодействия.

Структура, основанная на аддитивном разложении ANOVA, значительно повышает интерпретируемость модели RAN. Представление сложной функции в виде суммы основных эффектов и разреженных парных взаимодействий позволяет точно определить вклад каждого компонента в конечный результат. Это, в свою очередь, обеспечивает возможность точного управления поведением модели, позволяя изменять отдельные эффекты или взаимодействия для достижения желаемого результата без влияния на остальные части сети. Такая гранулярность контроля особенно полезна для задач, требующих высокой степени предсказуемости и объяснимости, например, в системах принятия решений или в задачах, связанных с безопасностью.

В архитектуре RAN, использование Residual Gating в сочетании с инициализацией весов близко к единичной матрице ( $I$ ) значительно повышает стабильность обучения и скорость сходимости. Такая инициализация позволяет избежать проблем, связанных с исчезающими или взрывающимися градиентами, особенно в глубоких сетях. Residual Gating, по сути, регулирует поток информации через сеть, позволяя более эффективно передавать градиенты обратно к начальным слоям, что ускоряет процесс обучения и улучшает общую производительность модели. Это достигается за счет добавления «остаточного» соединения, которое позволяет сигналу обходить некоторые слои, что способствует сохранению информации и стабилизации обучения.

В отличие от многослойных персептронов (MLP) с фиксированными активациями и KAN, использующих сплайны на ребрах, RAN применяет обучаемые рациональные единицы в топологии функционального ANOVA, что позволяет эффективно разлагать влияние факторов на основные эффекты (<span class="katex-eq" data-katex-display="false">P_i/Q_i</span>) и разреженные взаимодействия (<span class="katex-eq" data-katex-display="false">P_{ij}/Q_{ij}</span>). — В отличие от многослойных персептронов (MLP) с фиксированными активациями и KAN, использующих сплайны на ребрах, RAN применяет обучаемые рациональные единицы в топологии функционального ANOVA, что позволяет эффективно разлагать влияние факторов на основные эффекты ( $P_i/Q_i$ ) и разреженные взаимодействия ( $P_{ij}/Q_{ij}$ ).

Результаты и Обобщающая Способность: Подтверждение Возможностей RAN

Разработанная архитектура RAN продемонстрировала впечатляющие результаты в решении задач символьной регрессии на базе бенчмарка Feynman, успешно осваивая сложные физические уравнения. В ходе экспериментов, модель смогла с высокой точностью предсказывать результаты физических процессов, достигая среднеквадратической ошибки (RMSE) порядка $10^{-8}$ . Такая высокая точность указывает на способность RAN эффективно извлекать и моделировать скрытые закономерности в данных, что делает её перспективным инструментом для научных исследований и инженерных задач, требующих точного моделирования физических явлений. Успешное решение задач бенчмарка Feynman подтверждает потенциал RAN в области автоматизированного открытия научных знаний.

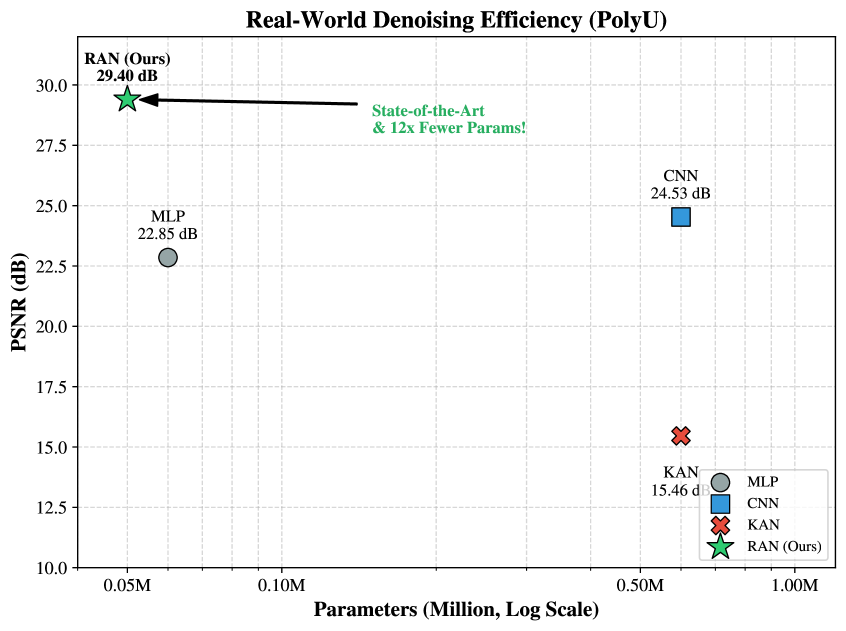
Оценка возможностей сети RAN проводилась с использованием протокола Kanbefair, который позволил продемонстрировать её надежную способность к обобщению на разнообразных наборах визуальных данных. Данный протокол, предназначенный для строгого тестирования обобщающей способности моделей, выявил устойчивость RAN к изменениям в данных и её способность успешно применять полученные знания к новым, ранее не встречавшимся изображениям. Результаты показали, что RAN эффективно адаптируется к различным визуальным задачам, сохраняя высокую точность и стабильность даже при значительных различиях в характеристиках используемых данных. Это свидетельствует о том, что сеть способна не просто запоминать обучающие примеры, но и извлекать общие закономерности, что является ключевым фактором для успешного применения в реальных условиях.

Исследования показали, что разработанная архитектура RAN значительно превосходит традиционные подходы, такие как сети Колмогорова-Арнольда (KAN), как по точности, так и по стабильности. На бенчмарке TabArena, RAN демонстрирует впечатляющую победу в 95% случаев, что свидетельствует о ее превосходстве в решении табличных задач. Примечательно, что RAN достигает сопоставимых результатов с существующими архитектурами, используя при этом на 5-7 операций меньше, что указывает на ее повышенную эффективность и потенциал для применения в ресурсоограниченных средах. Данное сочетание высокой производительности и сниженной вычислительной сложности делает RAN перспективной платформой для широкого спектра задач машинного обучения.

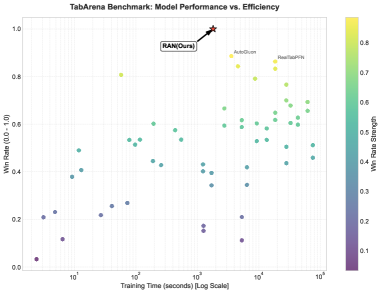
Разработанная модель RAN демонстрирует наивысший процент побед в TabArena, при этом время обучения на несколько порядков меньше, чем у ведущих базовых моделей, таких как AutoGluon и RealTabPFN.

Перспективы Развития: К Надежному и Интерпретируемому ИИ

В основе архитектуры RAN лежит принцип изометрии, что открывает новые возможности для создания моделей, устойчивых к незначительным изменениям входных данных и даже к целенаправленным атакам, направленным на искажение результатов. Изометрия, сохраняющая расстояния между точками в многомерном пространстве, позволяет сети более эффективно обобщать информацию и менее восприимчиво реагировать на небольшие возмущения, которые могли бы ввести в заблуждение менее устойчивые модели. Этот подход, в отличие от традиционных методов, где небольшие изменения во входных данных могут привести к значительным колебаниям в выходных данных, обеспечивает повышенную надежность и предсказуемость работы искусственного интеллекта в реальных условиях, где входные данные часто бывают зашумлены или неполны. Таким образом, использование изометрии в RAN представляет собой перспективный путь к созданию более надежных и безопасных систем искусственного интеллекта.

Дальнейшее развитие аддитивного разложения дисперсии ANOVA представляется перспективным путем к повышению прозрачности и управляемости искусственного интеллекта. В то время как традиционное ANOVA позволяет оценить вклад отдельных факторов в общую дисперсию, расширенные версии, интегрированные в архитектуры, подобные RAN, могут предоставить детальное понимание того, как каждый нейрон или группа нейронов влияет на окончательное решение модели. Это не только облегчает отладку и выявление потенциальных предвзятостей, но и открывает возможности для целенаправленного управления поведением системы. Использование подобных декомпозиций позволяет, например, модифицировать отдельные компоненты модели, не затрагивая остальные, что особенно ценно в критически важных приложениях, где требуется высокая степень надежности и предсказуемости. $\sum_{i=1}^{n} S_i = SST$ — фундаментальный принцип ANOVA, который, будучи расширен и адаптирован для сложных нейронных сетей, может стать ключом к созданию действительно интерпретируемых и контролируемых систем ИИ.

Стабильность процесса обучения, демонстрируемая Random Additive Networks (RAN) благодаря применению алгоритма градиентного спуска и L2-регуляризации, представляет собой важный прогресс в создании надежных и заслуживающих доверия систем искусственного интеллекта. Традиционные нейронные сети часто страдают от нестабильности при обучении, приводящей к непредсказуемым результатам и уязвимости к незначительным изменениям во входных данных. В отличие от них, RAN, благодаря своей архитектуре и использованным методам оптимизации, обеспечивает более предсказуемую и устойчивую сходимость. Это позволяет создавать модели, которые не только эффективно решают поставленные задачи, но и демонстрируют повышенную надежность и предсказуемость в различных условиях, что особенно важно для критически важных приложений, таких как автономное вождение или медицинская диагностика. Подобная стабильность открывает путь к разработке более безопасных и понятных систем ИИ, способных к долгосрочной и надежной работе.

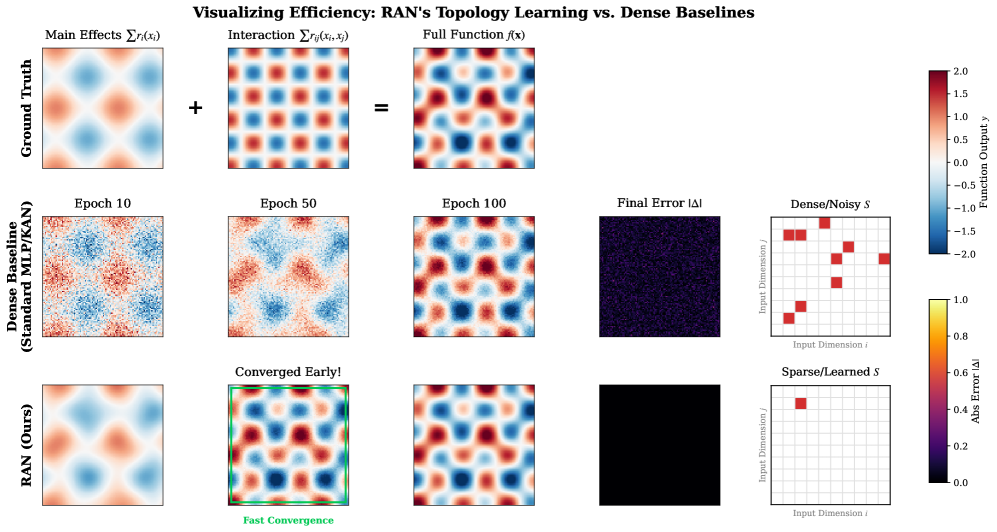
Анализ эволюции способности модели к обучению через топологию взаимодействий показывает, что эффективный отбор пар признаков с высокой связью градиента (RAN) позволяет быстрее сходиться к истинной функции даже при разреженной структуре, подтверждая важность качества связей, а не их количества.

Исследование, представленное в данной работе, демонстрирует стремление к созданию систем, где структура определяет поведение. Авторы, разрабатывая Rational-ANOVA Networks, акцентируют внимание на важности ясных границ и декомпозиции для достижения стабильности и интерпретируемости в глубоком обучении. Это согласуется с принципом, высказанным Брайаном Керниганом: “Не волнуйтесь о том, чтобы сделать что-то элегантное; просто сделайте это правильно.” В контексте Rational-ANOVA Networks, ‘сделать правильно’ означает создать архитектуру, в которой каждый компонент четко определен и способствует общей стабильности обучения, особенно в сложных задачах, таких как символьная регрессия. Подобный подход позволяет создавать системы, которые не только эффективно решают поставленные задачи, но и остаются понятными и предсказуемыми.

Куда Дальше?

Представленные Рациональные ANOVA-сети (RAN) демонстрируют интересное направление в стабилизации обучения глубоких нейронных сетей и повышении их интерпретируемости. Однако, кажущаяся элегантность архитектуры не должна заслонять фундаментальную проблему: оптимизация лишь симптомов, а не первопричины. Замена стандартных единиц на рациональные и применение ANOVA-декомпозиции — это, безусловно, шаг вперёд, но вопрос о природе градиентного взрыва и исчезающих градиентов остаётся открытым. Оптимизируется не то, что нужно, а то, что поддаётся оптимизации.

Будущие исследования должны сосредоточиться на более глубоком понимании динамики обучения, а не на создании всё более изощрённых архитектур. Простота масштабируется, изощрённость — нет. Интересным направлением представляется изучение связи между структурой сети и её устойчивостью к возмущениям, а также разработка методов автоматического поиска оптимальной структуры, основанных на принципах теории информации. Хорошая архитектура незаметна, пока не ломается.

Зависимости — настоящая цена свободы. Внедрение RAN, как и любой новой архитектуры, неизбежно влечёт за собой увеличение сложности и, следовательно, потенциальных точек отказа. Поэтому, параллельно с развитием новых методов, необходимо уделять внимание разработке инструментов для диагностики и отладки глубоких нейронных сетей, а также созданию более надёжных и устойчивых алгоритмов обучения.

Оригинал статьи: https://arxiv.org/pdf/2602.04006.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-05 10:07