Автор: Денис Аветисян
Исследователи представили алгоритм SWING, позволяющий эффективно аппроксимировать методы графовых ядер, используя случайные блуждания в непрерывном пространстве.

SWING эффективно приближает методы графовых ядер для неявных графов, значительно повышая вычислительную эффективность за счет использования случайных блужданий в непрерывном пространстве.
Вычисления на графах, заданных неявно, часто сталкиваются с ограничениями вычислительной сложности. В данной работе, озаглавленной ‘SWING: Unlocking Implicit Graph Representations for Graph Random Features’, предложен алгоритм SWING, использующий случайные блуждания в непрерывном пространстве для эффективной аппроксимации вычислений на графах, заданных функциями весов ребер. SWING позволяет избежать материализации графа и опирается на глубокую связь между неявными графами и Фурье-анализом, используя кастомизированный механизм семплирования Gumbel-softmax с линеаризованными ядрами. Может ли SWING стать ключевым инструментом для масштабирования графовых нейронных сетей и методов машинного обучения на больших и сложных неявных графах?
За гранью очевидного: Сложность измерения сходства графов
В современной машинном обучении, измерение сходства между данными, представленными в виде графов, играет ключевую роль во множестве задач — от поиска похожих молекул в химии до анализа социальных сетей и рекомендательных систем. Однако, традиционные методы вычисления сходства графов сталкиваются с серьезными ограничениями при работе с большими объемами данных. Сложность этих методов часто растет экспоненциально с увеличением размера графа, что делает их практически неприменимыми для анализа крупных сетевых структур. Это создает существенную проблему, поскольку возможность эффективного сравнения графов напрямую влияет на производительность и масштабируемость многих алгоритмов машинного обучения, ограничивая их применение в реальных сценариях, где данные постоянно растут и усложняются.
Прямые вычисления ядерных функций, являющихся основой многих мощных методов машинного обучения, сталкиваются с серьезными ограничениями при работе с графами большого размера. Сложность этих вычислений растет экспоненциально с увеличением числа вершин и ребер в графе, что делает их практически невозможными для реализации на современных вычислительных системах. Например, для графа с n вершинами, вычисление матрицы ядра может потребовать порядка O(n^3) операций, что быстро становится непосильной задачей. Это препятствует применению эффективных алгоритмов, основанных на ядрах, к задачам, где данные представлены в виде больших графов, таких как анализ социальных сетей, биоинформатика и обработка молекулярных структур. Таким образом, поиск приближенных, но вычислительно эффективных методов для оценки ядерных функций является критически важным для расширения возможностей графового машинного обучения.
Эффективная аппроксимация ядерных функций, сохраняя при этом необходимую точность, представляет собой ключевую проблему в машинном обучении на графах. Традиционные методы вычисления сходства между графами, основанные на прямом вычислении ядер, становятся непомерно затратными по вычислительным ресурсам при работе с крупными графами, что ограничивает применение мощных алгоритмов, таких как машины опорных векторов. Разработка алгоритмов, способных быстро и точно оценивать сходство графов, критически важна для масштабирования методов машинного обучения и решения практических задач в различных областях, включая анализ социальных сетей, биоинформатику и открытие лекарств. Ученые активно исследуют различные подходы к аппроксимации ядер, такие как случайные прогулки по графам и методы снижения размерности, стремясь найти оптимальный баланс между скоростью вычислений и точностью результата, что позволит эффективно использовать графовые данные в широком спектре приложений.
Графовые случайные признаки: Путь к эффективности вычислений
Графовые случайные признаки (Graph Random Features) представляют собой перспективное решение для снижения вычислительных затрат при работе с графами. Традиционные методы, использующие матрицу ядра, требуют O(n^3) операций для вычислений и O(n^2) памяти для хранения, где n — количество узлов в графе. Графовые случайные признаки позволяют разложить матрицу ядра на разреженное представление, заменяя её приближением, основанным на случайных признаках. Это приводит к снижению вычислительной сложности до O(nm), где m — количество случайных признаков и обычно значительно меньше n. В результате, операции, такие как вычисление спектральной декомпозиции или решение систем линейных уравнений, становятся практически осуществимыми для графов, которые ранее были недоступны из-за ограничений по памяти и вычислительной мощности.
Метод случайных признаков графа (Graph Random Features) позволяет эффективно аппроксимировать матрицу ядра, снижая вычислительные затраты при работе с большими графами. Вместо вычисления полного ядра, что требует O(n^2) операций для графа с n вершинами, аппроксимация с использованием случайных признаков сводит сложность к O(n*m), где m — размерность случайных признаков и, как правило, значительно меньше n. При этом, при правильном выборе параметров и количества признаков, потеря точности аппроксимации остается незначительной, что делает возможным применение методов ядра, таких как машины опорных векторов (SVM) и гауссовские процессы, к графам, которые ранее были недоступны из-за вычислительных ограничений.
Эффективность использования случайных признаков графа (Graph Random Features) напрямую зависит от качества полученного приближения и выбора самих случайных признаков. Недостаточное количество признаков может привести к существенной потере точности при аппроксимации ядра, в то время как избыточное количество увеличивает вычислительные затраты и сложность модели. Выбор конкретного семейства случайных признаков и параметров их генерации должен основываться на характеристиках графа и поставленной задаче, поскольку оптимальный вариант может различаться в зависимости от плотности графа, его структуры и требований к точности приближения K(x, y). Оценка качества приближения, например, путем анализа спектральной ошибки или путем сравнения результатов работы модели с использованием полного ядра и приближенного ядра, является важным шагом для обеспечения надежности и эффективности метода.
SWING: Непрерывные случайные блуждания для аппроксимации ядра
В отличие от традиционных методов аппроксимации графовых ядер, основанных на дискретных случайных блужданиях по узлам графа, SWING предлагает новый подход, использующий непрерывное пространство. Вместо перемещения между конкретными узлами, случайные блуждания моделируются в непрерывной области, что позволяет избежать проблем, связанных с дискретизацией и повысить гибкость. Такой подход позволяет более эффективно оценивать сходство между графами, особенно в случаях, когда структура графа сложна или имеет высокую размерность. Это достигается путем представления графа в виде непрерывного пространства, в котором случайные блуждания могут происходить без ограничений дискретной структуры.
Метод SWING использует матричную экспоненту и Gumbel-Softmax для реализации дифференцируемых и эффективных непрерывных случайных блужданий. Матричная экспонента exp(A) , где A — матрица смежности графа, позволяет моделировать вероятности переходов между узлами в непрерывном пространстве. Gumbel-Softmax, в свою очередь, выполняет роль дифференцируемой аппроксимации функции argmax, необходимую для выбора траектории случайного блуждания. Использование Gumbel-Softmax позволяет вычислять градиенты через случайные процессы, что критически важно для обучения моделей машинного обучения, использующих SWING в качестве ядра. Сочетание этих двух техник обеспечивает возможность эффективного и дифференцируемого моделирования непрерывных случайных блужданий, обходя ограничения дискретных методов.
В SWING для повышения эффективности вычислений применяется метод Importance Sampling. Этот подход позволяет сосредоточить вычислительные ресурсы на наиболее значимых путях случайных блужданий, отбрасывая менее важные траектории. Вместо равномерной выборки путей, Importance Sampling использует весовую функцию для оценки вклада каждого пути в конечное значение ядра. Веса определяются на основе вероятности каждого пути, что позволяет более эффективно использовать вычислительные ресурсы и снизить дисперсию оценки ядра. Таким образом, достигается более точная и быстрая аппроксимация ядра графа, особенно для больших графов, где полный перебор путей становится непрактичным.

Проверка SWING: Точность и эффективность на практике
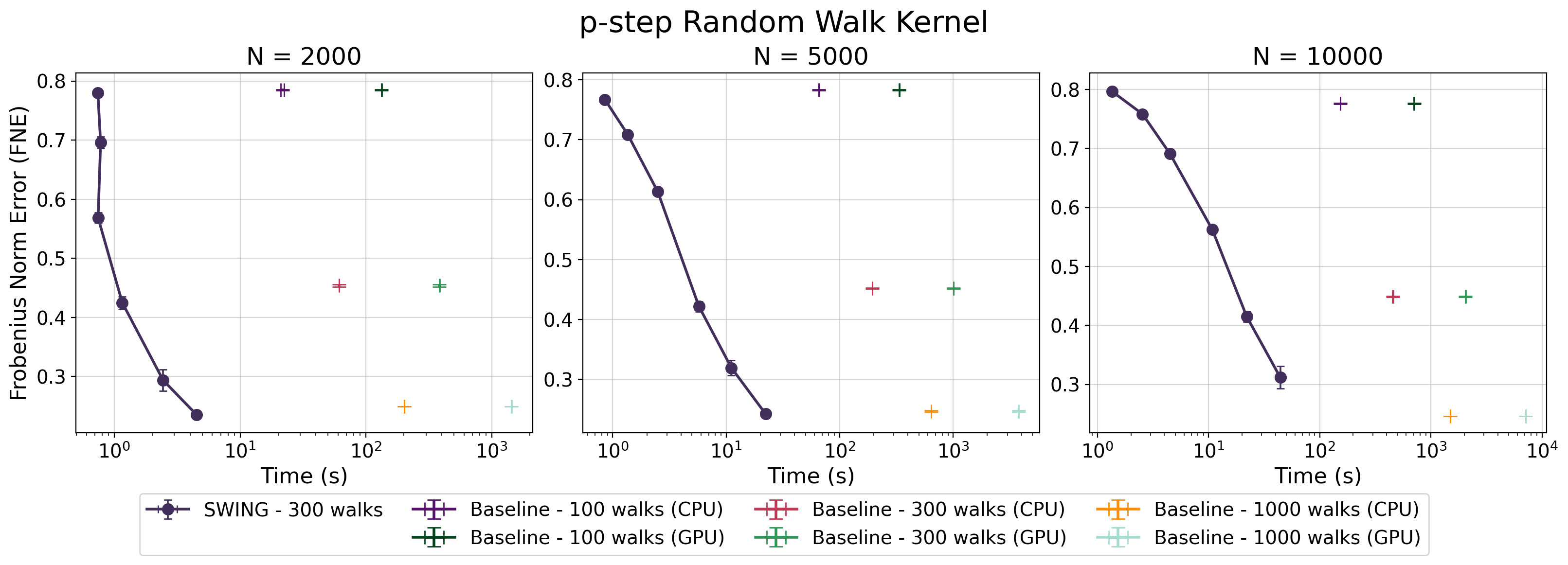
Тщательная оценка точности приближения ядра в SWING проводилась с использованием нормы Фробениуса, что позволило получить количественно измеримый показатель эффективности. Норма Фробениуса, \lVert A \rVert_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^2}, обеспечивает надежный способ оценки разницы между приближенным ядром, вычисленным SWING, и точным ядром, полученным традиционными методами. Данный подход позволяет объективно сравнивать производительность SWING с существующими алгоритмами, демонстрируя его способность обеспечивать высокую точность при вычислении ядра, что критически важно для корректной работы алгоритмов графовых случайных полей и других приложений, основанных на анализе данных, представленных в виде графов.
Исследования показали, что разработанный метод SWING демонстрирует сопоставимую точность с традиционными методами Gaussian Random Fields (GRF) при использовании различных ядер, включая случайные блуждания, диффузию и регуляризованный лапласиан, на синтетических облаках точек. Эта сравнимость достигается при обработке данных различной сложности и структуры, подтверждая надежность SWING как альтернативного подхода к анализу геометрических данных. Полученные результаты указывают на то, что SWING эффективно аппроксимирует ядро, обеспечивая достаточную точность для широкого спектра задач, требующих анализа формы и структуры, без ущерба для производительности по сравнению с устоявшимися методами GRF.
Исследования показали, что разработанный метод SWING обеспечивает значительное ускорение процесса вычислений по сравнению со стандартными методами GRF. В частности, зафиксировано десятикратное увеличение скорости вывода данных 10x при сохранении сопоставимой точности результатов. Более того, SWING демонстрирует улучшенное время построения ядра, особенно при увеличении размера обрабатываемой сетки, что делает его эффективным решением для работы с крупномасштабными данными и сложными геометрическими моделями. Данное преимущество в скорости и эффективности открывает новые возможности для применения графовых ядерных методов в областях, требующих обработки больших объемов данных в реальном времени.
Расширение горизонтов: Неявные графы и перспективы развития
Метод SWING демонстрирует значительную применимость к неявным графам, где связи между узлами не заданы явно, а выводятся на основе анализа данных. Это открывает широкие возможности для применения в разнообразных областях, где традиционные методы построения графов неэффективны или невозможны. Вместо явного определения ребер, SWING способен выявлять скрытые взаимосвязи, используя информацию, извлеченную непосредственно из данных, что особенно ценно при работе с комплексными системами, такими как социальные сети, биологические сети или сети рекомендаций. Такая гибкость позволяет анализировать структуры, которые ранее были недоступны для исследования с помощью стандартных алгоритмов анализа графов, существенно расширяя горизонты применения методов спектрального анализа графов.
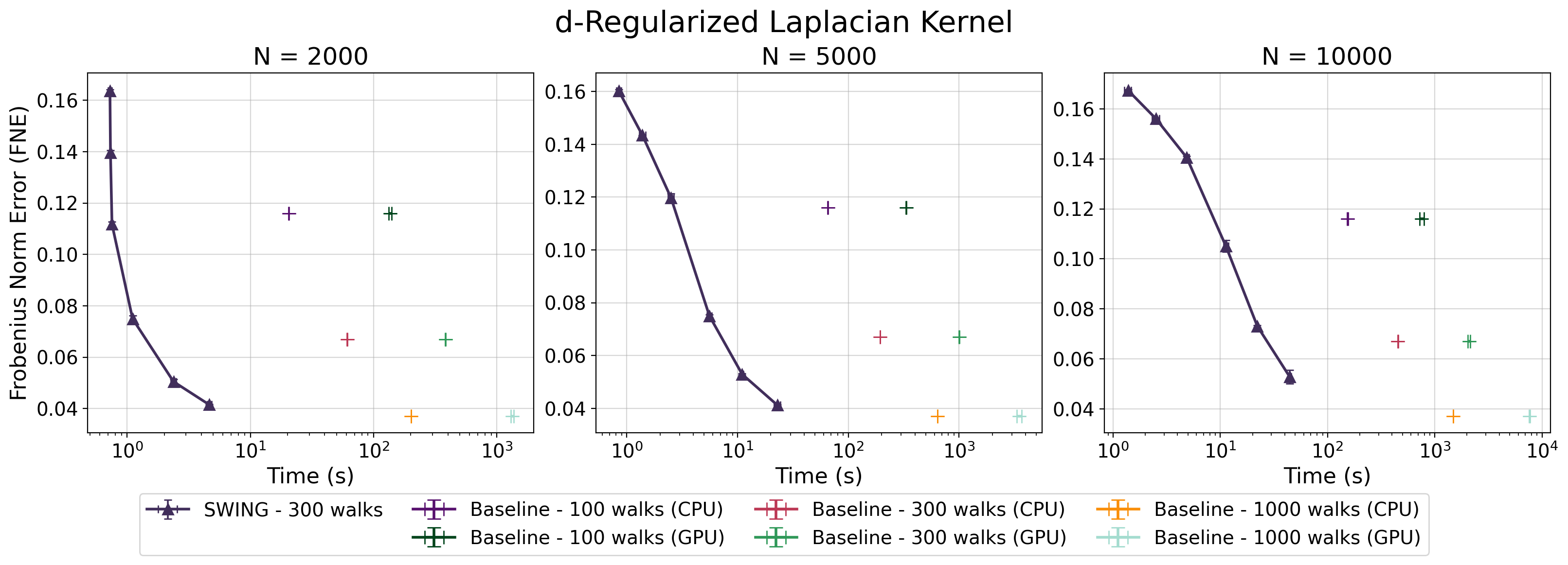
Метод SWING предоставляет эффективный способ аппроксимации ядра диффузии и регуляризованного лапласиана, что открывает новые горизонты в спектральном анализе графов. Традиционные вычисления этих ядер могут быть вычислительно затратными, особенно для больших графов. SWING позволяет существенно сократить эти затраты, используя приближенные вычисления без значительной потери точности. Это особенно важно для задач, требующих многократного вычисления ядер, таких как кластеризация, визуализация и обнаружение сообществ. Возможность эффективной аппроксимации \textbf{L} = \textbf{A} - \textbf{D} и связанных с ним операторов позволяет исследователям применять спектральные методы к более крупным и сложным графовым структурам, расширяя область их применения в различных областях, включая анализ социальных сетей, обработку изображений и машинное обучение.
Предстоящие исследования направлены на дальнейшую оптимизацию производительности SWING, с акцентом на повышение скорости вычислений и снижение потребления памяти. Особое внимание будет уделено изучению потенциала применения SWING в перспективных областях, таких как графовые нейронные сети, где эффективная обработка графовых данных имеет решающее значение. Кроме того, планируется исследовать возможности использования SWING в биоинформатике, в частности, для анализа сложных биологических сетей и выявления закономерностей в данных о генах и белках. Успешная реализация этих направлений позволит значительно расширить область применения SWING и внести вклад в развитие современных методов анализа графов и машинного обучения.
Исследование демонстрирует, что для эффективной работы с неявными графами необходимо отойти от традиционных методов, оперирующих дискретными узлами. Вместо этого, предлагается подход, основанный на непрерывных случайных блужданиях, что позволяет значительно снизить вычислительную сложность. Этот метод напоминает философское утверждение Бертрана Рассела: «Всё, что кажется само собой разумеющимся, следует подвергать сомнению». Подобно тому, как Рассел призывал к критическому мышлению, данная работа подвергает сомнению устоявшиеся подходы к работе с графами, предлагая новый, более эффективный способ представления и обработки информации, особенно в контексте неявных графов и методов случайных признаков.
Куда же это всё ведёт?
Представленный алгоритм SWING, безусловно, предлагает элегантный обход вычислительных сложностей, возникающих при работе с неявными графами. Однако, подобно любой новой карте, он лишь указывает на неизведанные территории, а не открывает их полностью. Вопрос о масштабируемости случайных блужданий в непрерывном пространстве для графов экстремально больших размеров остаётся открытым. Утверждать, что SWING — окончательное решение, было бы слишком самоуверенно; скорее, это — признание слабости существующих методов и вызов для дальнейших исследований.
Очевидным направлением является поиск способов адаптации алгоритма к динамически меняющимся графам. Если граф — это не статичная структура, а живой организм, то и метод аппроксимации должен быть способен к эволюции. Кроме того, взаимодействие SWING с другими методами машинного обучения, такими как глубокие нейронные сети, представляется плодотворной областью для экспериментов. В конце концов, всё сводится к поиску оптимального баланса между точностью, эффективностью и адаптивностью.
Возникает и философский вопрос: что есть «неявный граф» на самом деле? Если граф — это абстракция, то как далеко можно зайти в его «неявности», не потеряв связь с реальностью? Алгоритм SWING, подобно зеркалу, отражает эту неопределённость, предлагая инструмент для работы с призраками, а не с материей. И в этом — его истинная ценность.
Оригинал статьи: https://arxiv.org/pdf/2602.12703.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- SOL ПРОГНОЗ. SOL криптовалюта
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
- SUI ПРОГНОЗ. SUI криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- FARTCOIN ПРОГНОЗ. FARTCOIN криптовалюта
- HYPE ПРОГНОЗ. HYPE криптовалюта
2026-02-17 03:28