Прогнозирование временных рядов: новый взгляд на диффузионные модели

Автор: Денис Аветисян

В статье представлена инновационная методика прогнозирования временных рядов, основанная на диффузионных моделях и спектральном разложении данных.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал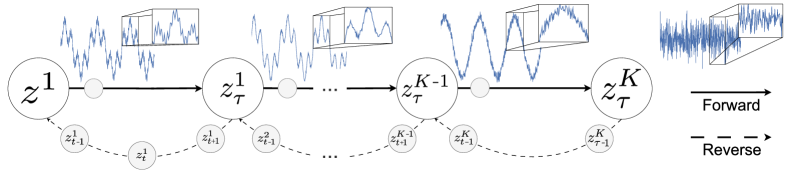

В процессе диффузии, разложение сигнала на компоненты с последовательным добавлением шума, начиная с наименее амплитудных, замедляет разрушение наиболее значимых частот и, следовательно, позволяет дольше сохранять ключевые структуры.

Предлагается декомпозируемый прямой процесс в диффузионных моделях для повышения точности прогнозирования, особенно на длительных временных горизонтах.

Несмотря на успехи диффузионных моделей во многих областях, прогнозирование временных рядов остается сложной задачей, особенно при долгосрочном планировании. В работе, озаглавленной ‘A Decomposable Forward Process in Diffusion Models for Time-Series Forecasting’, предложен новый подход, использующий разложение сигнала на спектральные компоненты непосредственно в процессе диффузии. Такой метод позволяет более эффективно сохранять структурированные временные закономерности, такие как сезонность, и повышать качество прогнозов. Может ли подобная декомпозиция стать ключевым элементом в создании более точных и надежных моделей прогнозирования временных рядов, способных адаптироваться к сложным и нелинейным динамикам?

Понимание Временных Рядов: Вызов Сложных Закономерностей

Точное прогнозирование временных рядов имеет решающее значение в самых разных областях — от финансов и экономики до метеорологии и управления цепочками поставок. Однако, традиционные методы анализа зачастую оказываются неэффективными при работе со сложными зависимостями, особенно когда речь идет о долгосрочных трендах и сезонности. Эти зависимости могут быть скрыты шумом и случайными колебаниями, что затрудняет выявление закономерностей и построение точных прогнозов. Неспособность адекватно учитывать эти сложные взаимосвязи приводит к значительным ошибкам в предсказаниях, что, в свою очередь, может повлечь за собой серьезные финансовые и операционные последствия для организаций, полагающихся на эти прогнозы.

Временные ряды часто демонстрируют сложные зависимости, обусловленные такими факторами, как сезонность и тренд. Однако, эти закономерности нередко маскируются остаточным шумом — случайными колебаниями, которые затрудняют выявление истинных сигналов. Этот шум, возникающий из-за не учтенных переменных или погрешностей измерений, существенно снижает эффективность прогностических моделей. Чем сильнее выражен остаточный шум по отношению к полезному сигналу, тем сложнее алгоритмам извлечь значимую информацию и построить точные прогнозы. Успешное фильтрование шума и выделение ключевых зависимостей — критически важная задача для повышения надежности прогнозирования во многих областях, от экономики и финансов до метеорологии и анализа медицинских данных.

Существующие подходы к анализу временных рядов часто оказываются неспособными в полной мере отразить их внутреннюю структуру, что приводит к неточным прогнозам. Традиционные методы, ориентированные на линейные зависимости, испытывают затруднения при работе с нелинейными и сложными взаимосвязями, присущими многим реальным процессам. Особенно остро эта проблема проявляется при наличии долгосрочных зависимостей и скрытых закономерностей, которые могут быть замаскированы шумом или нерегулярными колебаниями. Неспособность адекватно моделировать эти структуры приводит к тому, что прогнозы оказываются недостаточно точными, что критически важно в таких областях, как финансы, метеорология и прогнозирование спроса. Поэтому, разработка новых методов, способных выявлять и учитывать сложные зависимости во временных рядах, является важной задачей современной науки.

Масштабирование отношения сигнал/шум позволяет дольше сохранять различимость ключевых частот в сигнале, в отличие от ситуации, когда шум равномерно распределяется по всем компонентам, ухудшая их разделение, при использовании линейного графика с параметрами <span class="katex-eq" data-katex-display="false">0.002 < \beta < 0.02</span>. — Масштабирование отношения сигнал/шум позволяет дольше сохранять различимость ключевых частот в сигнале, в отличие от ситуации, когда шум равномерно распределяется по всем компонентам, ухудшая их разделение, при использовании линейного графика с параметрами $0.002 < \beta < 0.02$ .

Декомпозиция Времени: Сила Разложения

Перед проведением прогнозирования, применение методов разложения временных рядов позволяет выделить составляющие компоненты: тренд, сезонность и остаточный шум. Разложение необходимо для упрощения анализа и моделирования данных, поскольку каждая компонента характеризуется собственными свойствами и закономерностями. Тренд отражает долгосрочное изменение данных, сезонность — повторяющиеся колебания в фиксированные периоды времени, а остаточный шум представляет собой случайные отклонения, не объяснимые трендом или сезонностью. Идентификация и отделение этих компонентов позволяют построить более точные и интерпретируемые модели прогнозирования, а также выявить скрытые закономерности в данных.

Методы разложения временных рядов, такие как преобразование Фурье и вейвлет-преобразование, предлагают различные подходы к разделению сигнала на составляющие частоты. Преобразование Фурье, основанное на анализе сигнала в частотной области, эффективно для стационарных сигналов и выявления доминирующих частот. Вейвлет-преобразование, напротив, использует вейвлеты — короткие волны различной частоты и масштаба — что позволяет анализировать нестационарные сигналы и выявлять локальные изменения частотных характеристик во времени. Вейвлеты особенно полезны при анализе сигналов с резкими изменениями или переходными процессами, где преобразование Фурье может давать менее точные результаты. Выбор метода зависит от характеристик анализируемого временного ряда и целей исследования.

Оценка качества разложения временного ряда на компоненты — критически важный этап, позволяющий удостовериться в корректности выделения тренда, сезонности и остаточного шума. Одним из распространенных методов оценки является использование отношения сигнал/шум (Signal-to-Noise Ratio — SNR). $SNR = \frac{P_{сигнал}}{P_{шум}}$ , где $P_{сигнал}$ — мощность полезного сигнала, а $P_{шум}$ — мощность остаточного шума. Высокое значение SNR указывает на четкое разделение компонентов и надежность разложения, что необходимо для последующего анализа и прогнозирования. Низкое значение SNR может свидетельствовать о необходимости пересмотра параметров разложения или выбора иного метода.

Увеличение числа компонентов шумового расписания приводит к снижению гладкости процесса диффузии при фиксированных параметрах расписания.

Генеративное Прогнозирование: Диффузионные Процессы и Структурированное Обучение

Диффузионные процессы, являясь разновидностью генеративного моделирования, используются для прогнозирования будущих значений временных рядов посредством изучения распределения вероятностей, лежащего в основе данных. В отличие от детерминированных моделей, диффузионные процессы строят вероятностную модель данных, постепенно добавляя шум к исходному сигналу до тех пор, пока он не станет полностью случайным. Обучение модели заключается в обратном процессе — удалении шума и восстановлении исходного сигнала, что позволяет ей генерировать новые, правдоподобные образцы, а также прогнозировать будущие значения на основе изученного распределения. $p(x_t|x_{t-1})$ определяет процесс добавления шума, а обученная модель стремится аппроксимировать обратный процесс $p(x_{t-1}|x_t)$ .

Предлагаемый Структурированный Прямой Диффузионный Процесс (Structured Forward Diffusion Process) улучшает стандартные методы генеративного прогнозирования за счет интеграции разложенных компонентов временного ряда — тренда, сезонности и остаточного шума — непосредственно в процесс обучения. Вместо обучения на необработанных данных, модель обучается на декомпозированных компонентах, что позволяет ей более эффективно моделировать сложные зависимости во временном ряду. Разделение на тренд, сезонность и остаточный шум позволяет модели выделять и изучать каждый компонент отдельно, что повышает точность прогнозов и позволяет генерировать вероятностные прогнозы, учитывающие неопределенность, присущую временным рядам. Такой подход позволяет более адекватно учитывать долгосрочные зависимости и улучшает качество прогнозирования по сравнению с традиционными методами, работающими с полным временным рядом.

Структурированный подход к диффузионному прогнозированию позволяет модели более эффективно учитывать долгосрочные зависимости во временных рядах. Разложение исходного ряда на компоненты — тренд, сезонность и остаточный шум — позволяет модели независимо изучать и моделировать каждый компонент, что улучшает ее способность к экстраполяции и прогнозированию на длительные горизонты. Вместо прогнозирования непосредственно значений временного ряда, модель обучается генерировать вероятностные прогнозы, предоставляя не только точечные оценки, но и информацию о неопределенности, выраженную в виде распределения вероятностей вокруг прогнозируемых значений. Это достигается за счет использования свойств диффузионных процессов, позволяющих генерировать разнообразные и правдоподобные сценарии развития временного ряда.

Сравнение трех моделей на случайной выборке из датасета PTB-XL демонстрирует влияние разложения Фурье (FFT) на генерацию данных.

Валидация и Эффективность: Достижение Передовых Результатов

Для оценки эффективности предложенной модели использовался датасет PTB-XL, представляющий собой сложный эталон для прогнозирования клинических временных рядов. Данный набор данных, содержащий обширные записи физиологических параметров пациентов, позволяет всесторонне проверить способность модели к точному предсказанию будущих значений на основе исторических данных. Сложность PTB-XL обусловлена не только объемом и разнообразием представленных данных, но и наличием шумов, пропусков и нелинейных зависимостей, что делает его идеальным инструментом для выявления наиболее перспективных алгоритмов прогнозирования в клинической практике. Использование именно этого датасета подтверждает надежность и применимость предложенного подхода в реальных медицинских сценариях.

Предложенный подход продемонстрировал значительное превосходство над существующими методами в задачах прогнозирования клинических временных рядов, что подтверждено результатами оценки на наборе данных PTB-XL. Оценка проводилась с использованием метрик $CRPS$ (Continuous Ranked Probability Score) и среднеквадратичной ошибки $MSE$ (Mean Squared Error), по которым новая модель показала более низкие значения по сравнению с аналогами. Такое улучшение свидетельствует о повышенной точности и надежности прогнозов, что особенно важно для принятия обоснованных решений в медицинской практике и мониторинге состояния пациентов.

Способность модели генерировать точные вероятностные прогнозы имеет решающее значение для принятия решений в широком спектре приложений. В отличие от традиционных методов, предоставляющих лишь единичные прогнозы, данная модель предоставляет распределение вероятностей возможных исходов, что позволяет оценить риски и неопределенности, связанные с каждым вариантом. Это особенно важно в клинической практике, где врачи могут использовать вероятностные прогнозы для персонализированного лечения и принятия обоснованных решений о вмешательстве. Например, прогнозируя вероятность развития осложнений у пациента, можно своевременно предпринять профилактические меры. Точность вероятностных прогнозов напрямую влияет на качество принимаемых решений, оптимизируя использование ресурсов и улучшая исходы в различных областях, от здравоохранения до финансов и управления рисками.

За Пределами Прогнозирования: Основа для Продвинутого Анализа Временных Рядов

Интеграция структурированного диффузионного процесса с архитектурами, такими как модели пространства состояний (State Space Models), представляет собой перспективное направление для существенного повышения производительности и масштабируемости анализа временных рядов. Такой подход позволяет объединить преимущества диффузии — способность эффективно моделировать сложные зависимости и генерировать реалистичные образцы — с вычислительной эффективностью и способностью к обработке длинных последовательностей, характерными для моделей пространства состояний. Предполагается, что комбинирование этих двух мощных инструментов позволит создавать системы, способные не только предсказывать будущие значения временных рядов, но и эффективно обрабатывать большие объемы данных, а также адаптироваться к изменяющимся условиям, что открывает новые возможности для применения в различных областях, включая финансы, метеорологию и прогнозирование спроса.

Исследование комбинированного использования вариационных автоэнкодеров (VAE) и диффузионных процессов открывает перспективные пути для улучшения обучения представлений временных рядов. VAE, способные сжимать данные в латентное пространство и восстанавливать их, в сочетании с диффузионными моделями, которые постепенно добавляют шум и затем обучаются его удалять, позволяют создавать более устойчивые и информативные представления. Такой синергетический подход позволяет моделям улавливать сложные зависимости во временных данных, эффективно решая проблему потери информации при сжатии и обеспечивая генерацию реалистичных и правдоподобных временных рядов. Ожидается, что данная комбинация значительно повысит точность прогнозирования и позволит создавать более надежные модели для анализа сложных динамических систем.

Предложенный подход создает надежную основу для разработки более сложных моделей анализа временных рядов, способных учитывать сложные взаимосвязи и генерировать достоверные прогнозы. В отличие от традиционных методов, фокусирующихся на статистических свойствах данных, данная методология позволяет моделировать динамику временных рядов как процесс диффузии, что особенно эффективно при работе с нелинейными и нестационарными данными. Такая гибкость позволяет улавливать тонкие зависимости и долгосрочные тренды, что существенно повышает точность прогнозирования в различных областях, включая финансы, метеорологию и обработку сигналов. Возможность моделирования неопределенности, присущая диффузионным моделям, также позволяет оценивать риски и принимать более обоснованные решения на основе прогнозов, что делает данный подход особенно ценным для задач, требующих высокой надежности и точности.

Настройка параметра <span class="katex-eq" data-katex-display="false">eta_{\tau}</span> позволяет шумовому расписанию достигать значений, близких к нулю, при <span class="katex-eq" data-katex-display="false">t=\tau</span>, независимо от количества компонент и их амплитуды. — Настройка параметра $eta_{\tau}$ позволяет шумовому расписанию достигать значений, близких к нулю, при $t=\tau$ , независимо от количества компонент и их амплитуды.

Исследование, представленное в данной работе, демонстрирует глубокое понимание системности временных рядов. Авторы предлагают декомпозицию как ключевой элемент процесса диффузии, что позволяет сохранить структурированные компоненты сигнала и повысить точность прогнозирования на больших временных горизонтах. Этот подход перекликается с философским утверждением Гегеля: «То, что рационально, то и реально». В контексте данной работы, рациональное применение спектрального анализа в процессе диффузии действительно позволяет выявить и сохранить реальные закономерности во временных рядах, что, в свою очередь, обеспечивает более точные и надежные прогнозы. Тщательная проверка границ данных, как подчеркивают авторы, является неотъемлемой частью этого процесса, предотвращая появление ложных закономерностей и обеспечивая надежность результатов.

Куда двигаться дальше?

Представленная работа, несомненно, открывает новые горизонты в области диффузионных моделей для прогнозирования временных рядов. Однако, стоит признать, что кажущаяся элегантность разложения сигнала — это лишь первый шаг. Воспроизводимость результатов, как всегда, остаётся краеугольным камнем. Необходимо более глубокое исследование влияния различных методов спектрального разложения на стабильность и обобщающую способность модели. Зачастую, математическая красота алгоритма не гарантирует его надежность в реальных условиях.

Особый интерес представляет вопрос о масштабируемости предложенного подхода к многомерным временным рядам. Разложение, эффективное для одномерного сигнала, может оказаться вычислительно неподъёмным для данных высокой размерности. Поэтому, разработка адаптивных методов разложения, учитывающих структуру данных, представляется крайне важной задачей. Наблюдается тенденция к усложнению моделей, но истинный прогресс заключается в поиске простых и объяснимых решений.

В конечном счёте, успех данного направления будет определяться не только точностью прогнозов, но и способностью модели к интерпретации. Понимание, какие компоненты сигнала оказывают наибольшее влияние на прогноз, а не просто получение численного результата, является ключом к созданию действительно интеллектуальных систем прогнозирования. Поиск закономерностей — это и есть суть науки, а не просто гонка за метриками качества.

Оригинал статьи: https://arxiv.org/pdf/2601.21812.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-01 22:01