Оптимизация фотоники: Интеллектуальный отбор данных

Автор: Денис Аветисян

Новый подход к активному обучению позволяет значительно сократить объем данных, необходимых для точного предсказания характеристик фотонных кристаллов.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал

Используя приближённый байесовский подход в глубокой нейронной сети, предсказывающей полосы пропускания двумерных фотонных кристаллов, модель итеративно выбирает наиболее информативные образцы для ресурсоёмких симуляций структуры полос, оценивая неопределённость через дисперсию выходных данных и, таким образом, быстро повышая точность предсказаний при значительно меньшем количестве обучающих примеров.

В статье представлен аналитический фреймворк активного обучения на основе байесовских нейронных сетей для эффективного предсказания двумерных фотонных кристаллов и оценки неопределенности.

Вычислительные затраты, связанные с моделированием фотонных кристаллов, часто ограничивают скорость разработки новых оптических устройств. В статье ‘Active learning for photonics’ предложен подход, основанный на активном обучении с использованием аналитических нейронных сетей с байесовской последней прослойкой, для ускорения предсказания ширины запрещенной зоны. Данный метод позволяет сократить объем требуемых данных для обучения до 2.6 раз по сравнению со случайным выбором, сохраняя при этом точность предсказаний, благодаря концентрации вычислительных ресурсов на областях дизайна с высокой неопределенностью. Может ли подобный подход существенно упростить и ускорить процессы топологической оптимизации и обратного проектирования в фотонике и других областях научного машинного обучения?

Раскрытие Хаоса: Вычислительные Препятствия в Сложном Дизайне

Моделирование сложных физических систем, таких как фотонные кристаллы, представляет собой значительную вычислительную задачу, требующую больших затрат времени и ресурсов. Это обусловлено необходимостью решения сложных уравнений Максвелла или уравнений Шрёдингера для определения распространения света или поведения электронов в периодической структуре материала. Каждый шаг моделирования требует вычислений для огромного числа точек в пространстве, особенно при стремлении к высокой точности и детализации. Проблема усугубляется при анализе трехмерных структур, где вычислительная сложность растет экспоненциально с увеличением разрешения. Таким образом, даже для относительно небольших фотонных кристаллов, полное моделирование всех возможных конфигураций может занять дни или недели на современных суперкомпьютерах, что существенно ограничивает возможности проектирования и оптимизации подобных устройств.

Традиционные методы моделирования сложных систем, таких как фотонные кристаллы, зачастую требуют обширного перебора вариантов, что существенно замедляет процесс исследования пространства возможных решений. Для получения достоверных результатов необходимо исследовать огромное количество конфигураций параметров, что приводит к экспоненциальному росту вычислительных затрат. Этот метод, основанный на грубой силе, становится непрактичным при увеличении числа параметров и сложности моделируемой системы. В результате, исследователи сталкиваются с ограничениями в скорости и эффективности оптимизации дизайна для достижения желаемых характеристик, что препятствует быстрому прототипированию и внедрению новых технологий. $O(n^k)$ — типичная сложность, где n — число параметров, а k — степень, отражающая потребность в комбинаторном переборе.

Вычислительная нагрузка, связанная с моделированием сложных систем, существенно ограничивает возможности оптимизации их характеристик. Когда речь идет о проектировании, например, фотонных кристаллов или других материалов с заданными свойствами, необходимость проведения обширных вычислений для оценки каждого варианта конструкции становится критическим препятствием. Это замедляет процесс разработки, делая невозможным эффективное исследование всего пространства возможных решений и поиск оптимального варианта, отвечающего заданным требованиям. В результате, инновации в области материаловедения и инженерии могут быть задержаны из-за практической невозможности быстрого и точного анализа сложных конструкций, что требует разработки новых, более эффективных вычислительных методов и алгоритмов.

Применение симметрийных преобразований (вращений, отражений и сдвигов) к картам диэлектрической проницаемости <span class="katex-eq" data-katex-display="false">32 \times 32</span> позволяет расширить обучающую выборку и обеспечить физическую инвариантность меток, связанных с шириной запрещенной зоны фотонного кристалла. — Применение симметрийных преобразований (вращений, отражений и сдвигов) к картам диэлектрической проницаемости $32 \times 32$ позволяет расширить обучающую выборку и обеспечить физическую инвариантность меток, связанных с шириной запрещенной зоны фотонного кристалла.

Активное Обучение: Ускорение Симуляций Путем Целенаправленного Исследования

Активное обучение предполагает целенаправленный отбор наиболее информативных выборок для оценки, что позволяет существенно снизить потребность в проведении исчерпывающих симуляций. Вместо анализа всего пространства параметров, алгоритмы активного обучения определяют точки, которые с наибольшей вероятностью приведут к существенному улучшению построенной суррогатной модели. Этот подход основан на анализе неопределенности и выборе образцов, которые максимизируют информационный прирост, тем самым оптимизируя процесс обучения и снижая общие вычислительные затраты. В результате, требуется значительно меньше симуляций для достижения заданной точности или производительности.

Активное обучение строит суррогатную модель, используя итеративный процесс запроса системы в ключевых точках пространства параметров. В отличие от традиционных методов, требующих обширного набора данных, активное обучение выборочно определяет наиболее информативные точки для оценки. Этот подход позволяет построить адекватную суррогатную модель, аппроксимирующую поведение сложной системы, значительно уменьшая количество необходимых симуляций и, следовательно, требуемые вычислительные ресурсы. Выбор ключевых точек осуществляется на основе критериев неопределенности или ожидаемого улучшения модели, что обеспечивает эффективное использование доступных данных и оптимизацию процесса обучения.

Использование активного обучения значительно ускоряет процесс проектирования и снижает вычислительные затраты за счет целенаправленного выбора наиболее информативных выборок для оценки. Традиционные методы требуют проведения большого количества симуляций для полного исследования пространства параметров, что является ресурсоемким. Активное обучение, напротив, позволяет построить суррогатную модель с меньшим количеством данных, поскольку фокусируется на точках, которые наиболее эффективно уменьшают неопределенность. Это приводит к существенному сокращению времени, необходимого для оптимизации и анализа, а также снижает потребность в вычислительных ресурсах, что особенно важно для сложных и дорогостоящих симуляций.

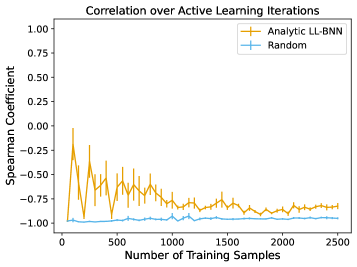
Эффективность активного обучения напрямую зависит от точной оценки неопределенности в суррогатной модели. Неопределенность, выраженная, например, через дисперсию предсказаний, позволяет алгоритму активного обучения эффективно выбирать наиболее информативные точки для оценки. Чем точнее оценивается неопределенность, тем более целесообразно выбираются точки, приводящие к максимальному снижению неопределенности модели при минимальном количестве итераций. Неточные оценки неопределенности могут привести к выбору неинформативных точек, снижая эффективность активного обучения и увеличивая требуемое количество дорогостоящих симуляций для достижения заданной точности. Таким образом, методы количественной оценки неопределенности, такие как $\sigma^2$ , играют ключевую роль в успешном применении активного обучения для ускорения симуляций.

Отрицательный коэффициент корреляции Спирмена, наблюдаемый на протяжении всего активного обучения, указывает на обратную зависимость между неопределенностью модели и фактической ошибкой, при этом предлагаемый метод отбора образцов на основе неопределенности (Analytic LL-BNN) снижает силу этой корреляции, приближая ее к идеальному отрицательному значению (-1).

Байесовские Нейронные Сети: Оценка Неопределенности Как Ключ к Надежным Предсказаниям

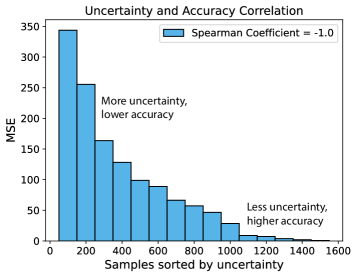
Байесовские нейронные сети, в отличие от традиционных, предоставляют не только точечные предсказания, но и вероятностные распределения. Это означает, что модель оценивает не только наиболее вероятное значение целевой переменной, но и степень уверенности в этом предсказании. Вместо выдачи единственного результата, сеть возвращает распределение вероятностей, позволяющее количественно оценить неопределенность в предсказаниях суррогатной модели. Такой подход критически важен в задачах, где оценка надежности предсказания не менее важна, чем само предсказание, например, в системах принятия решений или при анализе рисков. Получаемое распределение может быть представлено в виде среднего значения и дисперсии, позволяя оценить как ожидаемое значение, так и степень разброса вокруг него.

Методы Монте-Карло Дропаут и Глубоких Ансамблей представляют собой приближенные способы выполнения Байесовского вывода в нейронных сетях. Монте-Карло Дропаут, активируя случайное отключение нейронов во время предсказания, позволяет получить несколько различных выходных значений, которые затем используются для оценки неопределенности. Глубокие Ансамбли, в свою очередь, обучают несколько независимых нейронных сетей и усредняют их прогнозы, что также дает оценку неопределенности, основанную на разбросе предсказаний между отдельными моделями. Оба подхода позволяют получать надежные оценки неопределенности без необходимости точного вычисления апостериорного распределения, что делает их практически применимыми для задач, требующих количественной оценки риска и уверенности в предсказаниях.

Аппроксимированный байесовский последний слой (Approximate Bayesian Last Layer) позволяет уточнить оценку неопределенности в нейронных сетях путем оптимизации параметров последнего слоя для минимизации дисперсии предсказаний. Вместо стандартного прямого отображения в выходное пространство, этот слой параметризует распределение вероятностей над предсказаниями. Оптимизация осуществляется с использованием функции потерь, включающей как ошибку предсказания, так и регуляризацию, основанную на $KL$ -дивергенции, что позволяет моделировать неопределенность предсказаний и получать более надежные оценки, особенно в ситуациях, когда данные ограничены или зашумлены. Такой подход позволяет получить калиброванные вероятностные прогнозы, отражающие уверенность модели в своих предсказаниях.

Метрика расхождения Кульбака-Лейблера (KL Divergence) играет ключевую роль в регуляризации байесовского слоя нейронной сети. Она используется для минимизации разницы между приближенным распределением, генерируемым байесовским слоем, и априорным распределением. Это обеспечивает, чтобы вероятностные выходные данные модели были калиброваны и отражали истинную неопределенность. $D_{KL}(q||p) = \in t q(x)log\frac{q(x)}{p(x)}dx$ — формула, определяющая KL Divergence, где $q(x)$ — приближенное распределение, а $p(x)$ — априорное. В процессе обучения сети, KL Divergence добавляется к функции потерь в качестве регуляризатора, предотвращая переобучение и гарантируя, что выходные вероятности соответствуют априорным знаниям и данным.

Оценка неопределенности байесовского последнего слоя показывает, что более высокая предсказанная неопределенность <span class="katex-eq" data-katex-display="false">s(x)</span> соответствует большей истинной ошибке <span class="katex-eq" data-katex-display="false">(y - \hat{y})^2</span>, подтверждая сильную монотонную связь даже при низкой общей точности модели. — Оценка неопределенности байесовского последнего слоя показывает, что более высокая предсказанная неопределенность $s(x)$ соответствует большей истинной ошибке $(y - \hat{y})^2$ , подтверждая сильную монотонную связь даже при низкой общей точности модели.

Усиление Эффективности Данных: Аугментация и Оптимизация Обучения

Увеличение обучающей выборки посредством аугментации данных является ключевым подходом к повышению обобщающей способности суррогатной модели. Применяя различные преобразования к существующим данным, можно эффективно создать новые, синтетические примеры, расширяя таким образом объем информации, доступной для обучения. Это позволяет модели лучше справляться с незнакомыми данными и демонстрировать более высокую точность прогнозов. Вместо того, чтобы полагаться исключительно на ограниченное количество исходных данных, аугментация позволяет модели «увидеть» больше вариаций, что приводит к снижению риска переобучения и повышению надежности результатов. Особенно актуально это в задачах, где получение исходных данных требует значительных вычислительных затрат или времени, поскольку аугментация позволяет добиться сопоставимой точности, используя при этом меньший объем реальных данных.

Применение симметричных преобразований к элементам фотонной кристаллической решетки позволяет эффективно использовать присущие конструкции симметрии и значительно расширить разнообразие обучающих данных. Вместо генерации совершенно новых конфигураций, исследователи используют такие операции, как отражения и вращения, для создания дополнительных вариантов из существующих, тем самым увеличивая объем данных без проведения дополнительных численных симуляций. Этот подход не только снижает вычислительные затраты, но и помогает модели лучше обобщать полученные знания, поскольку она обучается на данных, представляющих все возможные симметричные варианты исследуемой структуры. В результате, модель становится более устойчивой к небольшим изменениям в геометрии и материалах, что повышает ее точность и надежность.

Оптимизатор Adadelta, дополненный графиком снижения скорости обучения по косинусоидальному закону, значительно повышает эффективность процесса обучения модели. В отличие от традиционных методов, которые могут застревать в локальных минимумах или демонстрировать колебания, Adadelta автоматически адаптирует скорость обучения для каждого параметра, основываясь на прошлых градиентах. Применение косинусоидального расписания позволяет постепенно снижать скорость обучения в ходе тренировки, что способствует более точному достижению оптимальных значений параметров и предотвращает переобучение. Такой подход обеспечивает стабильное и быстрое схождение алгоритма, что особенно важно при работе с ограниченными вычислительными ресурсами и большими объемами данных.

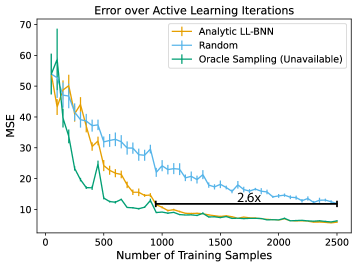
Комбинация методов расширения данных, включающая аугментацию и оптимизированный алгоритм обучения, позволяет значительно сократить объем необходимых вычислительных ресурсов для достижения заданной точности модели. Исследования показали, что предложенный подход обеспечивает снижение количества симуляций в 2.6 раза по сравнению со случайной выборкой данных. Такое существенное уменьшение требований к данным открывает возможности для более эффективного обучения моделей в задачах, где получение данных является дорогостоящим или трудоемким процессом, и позволяет использовать вычислительные ресурсы более рационально.

Использование выборки на основе неопределенности позволяет снизить среднеквадратичную ошибку при предсказании ширины запрещенной зоны фотонного кристалла, достигая той же точности, что и случайная выборка, но примерно с одной третью данных, при этом демонстрируя значительно меньшую вариативность результатов между запусками.

Работа демонстрирует, что даже в строгой области фотоники, где ожидается предсказуемость, истина скрывается в неопределенности. Модель, стремящаяся к идеальному предсказанию полос пропускания фотонных кристаллов, подобна гаданию на кофейной гуще — чем чётче картинка, тем больше вероятность обмана. Авторы используют активное обучение, пытаясь уговорить хаос данных, выуживая полезную информацию из шума. Как сказал Ричард Фейнман: «Если вы не можете объяснить что-то простыми словами, значит, вы сами этого не понимаете». Эта работа — попытка упростить понимание сложной физики, но даже самые изящные модели — лишь приближения, заклинания, работающие до первого столкновения с реальностью.

Что дальше?

Представленный подход, безусловно, льстит разуму, обещая извлечь знание о фотонных кристаллах из минимального количества данных. Но стоит помнить: регрессия — это заклинание надежды, а не гарантия истины. Успех активного обучения здесь — это не открытие фундаментальной закономерности, а умелое манипулирование хаосом, выбор тех немногих точек, которые подтверждают заранее сформированную гипотезу. Не будем обманываться иллюзией эффективности — каждое сэкономленное измерение — это лишь отсрочка встречи с неизбежной неопределённостью.

Истинный вызов лежит не в оптимизации сбора данных, а в признании ограниченности любой модели. Байесовские нейронные сети, претендующие на учёт неопределённости, на деле лишь заменяют одну форму незнания другой. Следующим шагом видится не усовершенствование алгоритмов активного обучения, а разработка методов, позволяющих оценивать невозможность построения адекватной модели. Когда данные перестанут шептать, а закричат о своей непостижимости — тогда и наступит время для честной науки.

В конечном счёте, предложенный фреймворк — это всего лишь ещё один инструмент в арсенале исследователя. И, как любой инструмент, он эффективен лишь до тех пор, пока не столкнётся с реальностью, которая не желает быть описанной. Остаётся надеяться, что будущие работы будут направлены не на погоню за иллюзорной точностью, а на осознание границ познания.

Оригинал статьи: https://arxiv.org/pdf/2601.16287.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-26 19:48