Нейросети: от классики к топологии в условиях неопределенности

Автор: Денис Аветисян

Новый обзор исследует, как современные методы машинного обучения, включая топологический анализ данных, могут повысить надежность и эффективность искусственного интеллекта в критических приложениях.

🐢

Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.

Телеграм канал

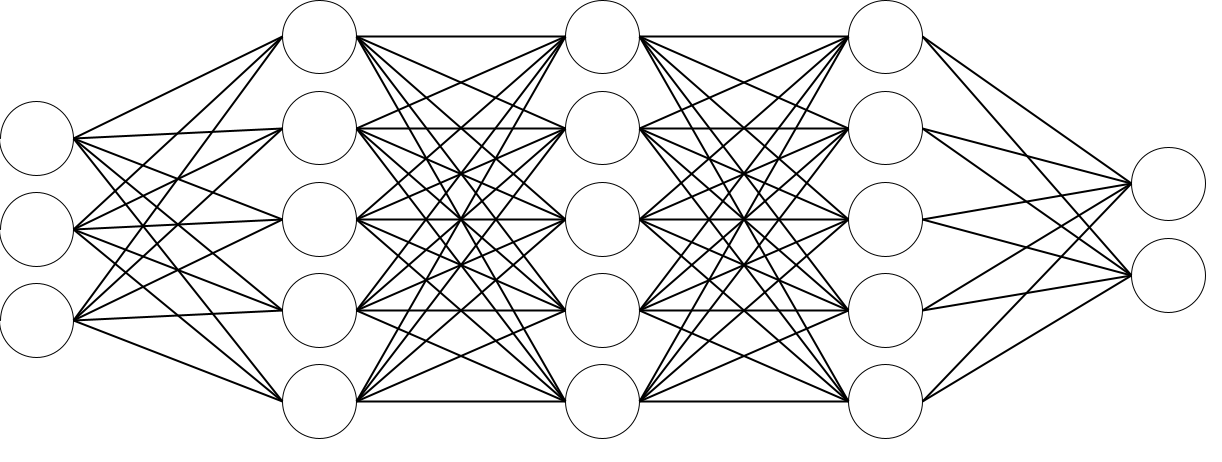
Искусственная нейронная сеть представляет собой вычислительную модель, организованную по принципу взаимосвязанных узлов, имитирующих биологические нейроны, что позволяет ей обрабатывать информацию и обучаться на основе данных.

Интеграция байесовских методов, графовых нейронных сетей и топологического анализа данных для повышения устойчивости и точности нейросетевых моделей в условиях неопределенности.

Несмотря на успехи классических нейронных сетей, их устойчивость к неопределенности и интерпретируемость остаются серьезными вызовами. В работе ‘From Classical to Topological Neural Networks Under Uncertainty’ исследуется интеграция искусственных нейронных сетей, байесовских методов, топологического анализа данных и графовых нейронных сетей для повышения эффективности систем искусственного интеллекта, в частности в военной сфере. Показано, что учет топологических свойств данных и квантификация неопределенности позволяют создавать более надежные и обобщающие модели для анализа изображений, временных рядов и графов. Какие новые перспективы открывает комбинирование этих подходов для решения задач, требующих высокой степени достоверности и интерпретируемости результатов?

Искусственный интеллект: от нейронных сетей к когнитивным моделям

Искусственный интеллект, как область исследований, ставит перед собой амбициозную задачу — воссоздать когнитивные способности человека посредством вычислительных моделей. Это предполагает не просто имитацию отдельных функций, таких как распознавание образов или решение логических задач, но и создание систем, способных к обучению, адаптации и даже творчеству. В основе этого подхода лежит идея о том, что интеллект — это, по сути, обработка информации, и, следовательно, его можно воспроизвести, разработав алгоритмы и структуры данных, способные выполнять аналогичные операции. Попытки моделирования когнитивных процессов охватывают широкий спектр областей, от машинного обучения и обработки естественного языка до компьютерного зрения и робототехники, стремясь создать системы, которые могут понимать, рассуждать и действовать в сложных и непредсказуемых условиях, подобно человеческому разуму.

Нейронные сети, являясь основой современных интеллектуальных систем, заимствуют принципы организации человеческого мозга. Эти сети состоят из множества взаимосвязанных узлов, называемых нейронами, которые обрабатывают и передают информацию, подобно биологическим нейронам. Связи между нейронами имеют веса, которые изменяются в процессе обучения, позволяя сети адаптироваться к новым данным и решать сложные задачи. Изначально вдохновленные упрощенной моделью работы мозга, нейронные сети эволюционировали в разнообразные архитектуры, такие как многослойные перцептроны, сверточные нейронные сети и рекуррентные нейронные сети, каждая из которых оптимизирована для конкретных типов задач, от распознавания изображений до обработки естественного языка. Их способность к обучению и адаптации делает их ключевым элементом в развитии искусственного интеллекта, открывая возможности для создания систем, способных к самостоятельному решению проблем и принятию решений.

Первые успехи свёрточных нейронных сетей (CNN) и рекуррентных нейронных сетей (RNN) продемонстрировали значительный потенциал в решении задач, связанных с обработкой изображений и последовательностей данных, соответственно. Однако, несмотря на впечатляющие результаты в отдельных областях, эти архитектуры зачастую испытывают трудности при работе со сложными, взаимосвязанными данными, требующими понимания контекста и отношений между различными элементами. Ограничения проявляются в способности эффективно моделировать знания, основанные на логических умозаключениях и здравом смысле, а также в сложности обработки данных, где важна не только последовательность, но и иерархия связей. Исследования показывают, что для преодоления этих ограничений необходимы новые архитектуры и методы обучения, способные учитывать реляционные аспекты данных и обеспечивать более глубокое понимание контекста.

Графовые нейронные сети: моделирование взаимосвязей для повышения интеллекта

Графовые нейронные сети (GNN) представляют собой расширение традиционных нейронных сетей, предназначенное для непосредственной работы со структурированными данными в виде графов. В отличие от стандартных сетей, принимающих данные в форме векторов или матриц, GNN способны обрабатывать и анализировать взаимосвязи между объектами, представленными в виде узлов и ребер графа. Это позволяет моделям учитывать не только атрибуты отдельных сущностей, но и контекст их взаимосвязей, что особенно важно для задач, где отношения между данными играют ключевую роль, например, в социальных сетях, молекулярной биологии и системах рекомендаций. Данный подход позволяет GNN эффективно моделировать сложные зависимости и извлекать информацию из данных, структура которых выходит за рамки традиционных форматов.

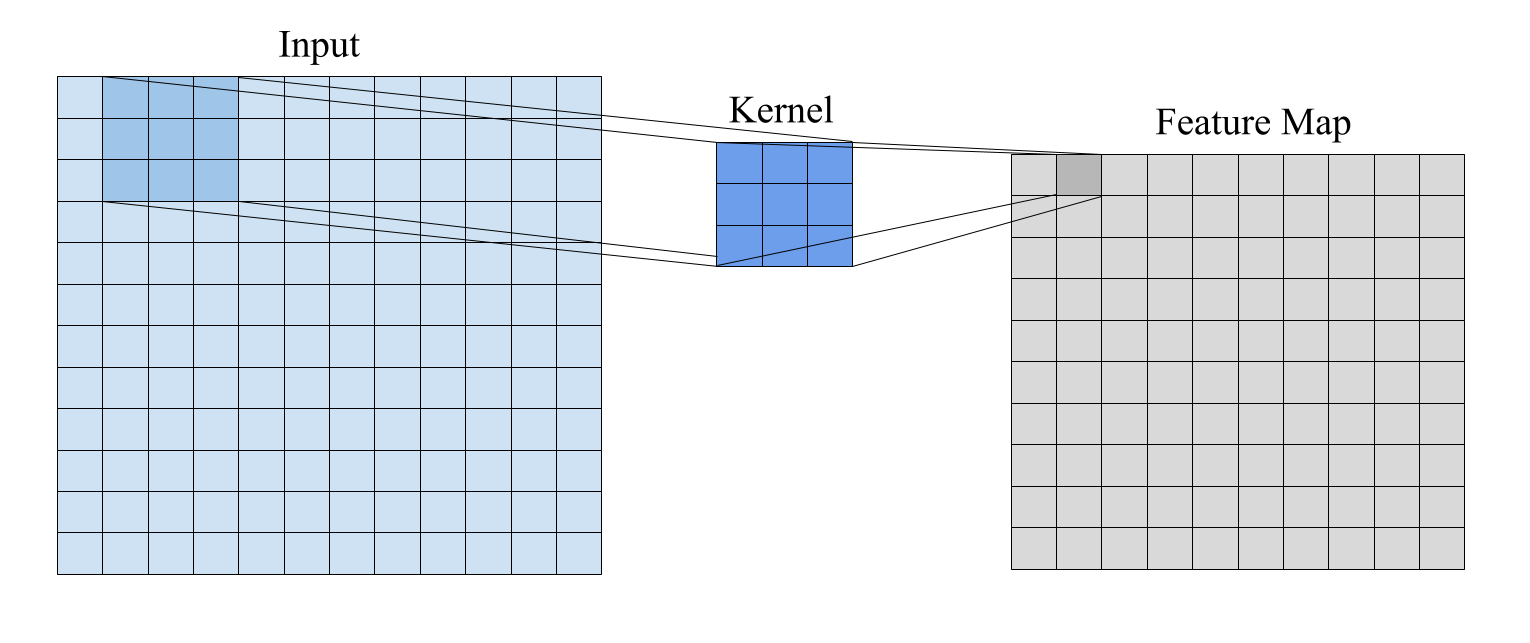
Сетевые нейронные сети, использующие свертки на графах (Graph Convolutional Networks, GCN), применяют спектральный подход к агрегации информации из локальных окрестностей каждого узла в графе. Этот подход основан на представлении графа в спектральной области с использованием матрицы Лапласа $L = D - A$ , где $A$ — матрица смежности, а $D$ — диагональная матрица степеней узлов. Свертка на графе определяется как $H = σ(D<sup>-1/2</sup>LD<sup>-1/2</sup>XW)$ , где $X$ — матрица признаков узлов, $W$ — матрица весов, а σ — функция активации. Данная операция эффективно фильтрует и агрегирует признаки соседних узлов, формируя новое представление для каждого узла, учитывающее его локальную структуру и связи.

Проблемы масштабируемости при работе с большими графами привели к разработке алгоритмов GraphSAGE и GraphSAINT, использующих методы сэмплирования для снижения вычислительных затрат и уменьшения смещения. GraphSAGE (Graph Sample and Aggregate) строит представления узлов путем агрегации признаков из локального окружения, выбранного случайным образом из соседей, что позволяет обрабатывать графы, где не все узлы доступны одновременно. GraphSAINT (Graph Sample and Imply) использует двухуровневую сэмплинг-стратегию — выбор подмножества узлов и их соседей — для эффективного вычисления агрегации признаков. Оба подхода направлены на уменьшение вычислительной сложности, сохраняя при этом качество представления графа, особенно в сценариях, где полный граф не помещается в память или требует чрезмерных ресурсов для обработки.

Свёртка, применяемая в свёрточном слое, позволяет извлекать признаки из входных данных путем скользящего применения фильтра.

Байесовские подходы к глубокому обучению: неопределенность и надежность

Байесовская статистика предоставляет формализованный подход к включению априорных знаний и количественной оценке неопределенности в прогнозах модели. В отличие от классической статистики, которая рассматривает параметры модели как фиксированные, но неизвестные значения, байесовский подход рассматривает их как случайные величины, описываемые вероятностными распределениями. Это позволяет не только оценить наиболее вероятные значения параметров, но и определить степень уверенности в этих оценках. Формально, это реализуется через теорему Байеса, которая позволяет обновить априорное распределение вероятностей параметров модели на основе наблюдаемых данных, получая апостериорное распределение $p(\theta|D) = \frac{p(D|\theta)p(\theta)}{p(D)}$ , где θ — параметры модели, $D$ — данные, $p(D|\theta)$ — правдоподобие, а $p(\theta)$ — априорное распределение. Таким образом, байесовская статистика обеспечивает не только точечные оценки, но и информацию о неопределенности, выраженную в виде дисперсии или доверительных интервалов.

Байесовские нейронные сети (БНС) отличаются от традиционных нейронных сетей тем, что рассматривают веса сети не как фиксированные значения, а как вероятностные распределения. Вместо одной оценки для каждого веса, БНС определяют распределение вероятностей для каждого параметра модели. Это позволяет учесть неопределенность в оценках весов, возникающую из-за ограниченности данных или сложности модели. В результате, предсказания БНС также представлены в виде распределений вероятностей, что позволяет оценить уверенность модели в своих предсказаниях и повысить устойчивость системы к шумам и неполноте данных. Такой подход обеспечивает более надежные и отказоустойчивые системы искусственного интеллекта, особенно в критически важных приложениях, где необходимо учитывать риски, связанные с неверными предсказаниями.

Байесовские нейронные сети, в отличие от стандартных, способны предоставлять не только точечные прогнозы, но и интервалы уверенности для этих прогнозов. Это достигается за счет представления параметров модели в виде вероятностных распределений, что позволяет оценить степень неопределенности в предсказаниях. Модели, выдающие широкие интервалы уверенности, сигнализируют о низкой уверенности в предсказании, указывая на потенциальную ненадежность результата. В критически важных приложениях, таких как медицинская диагностика или автономное вождение, возможность идентификации ненадежных предсказаний позволяет принять меры предосторожности или запросить дополнительную информацию, существенно повышая безопасность и надежность системы. Формально, интервал уверенности $[μ - kσ, μ + kσ]$ определяет диапазон, в котором, с заданной вероятностью, находится истинное значение, где μ — среднее значение, σ — стандартное отклонение, а $k$ — коэффициент, определяющий уровень доверия.

Топология и глубокое обучение: раскрытие скрытой структуры данных

Топологический анализ данных (TDA) представляет собой набор математических инструментов, предназначенных для выявления скрытых структур и формы в сложных данных. В отличие от традиционных методов, которые фокусируются на метрических свойствах, таких как расстояния, TDA исследует инвариантные характеристики, сохраняющиеся при непрерывных деформациях. Это позволяет выявлять такие особенности, как петли, дыры и связность, которые могут быть критически важны для понимания данных, даже если их точное положение или размер меняются. $\mathbb{Z}_2$ -гомологии, например, позволяют определить количество несвязанных компонентов и «дыр» в данных, независимо от их геометрической реализации. Такой подход особенно ценен при анализе данных высокой размерности, где традиционные методы могут оказаться неэффективными, и позволяет обнаруживать неявные связи и закономерности, которые иначе могли бы остаться незамеченными.

Интеграция топологического анализа данных (TDA) с методами глубокого обучения, известная как Топологическое Глубокое Обучение, открывает новые возможности для анализа сложных данных. Традиционные нейронные сети часто испытывают трудности с улавливанием зависимостей между удаленными элементами данных, однако TDA предоставляет инструменты для выявления и использования этих нелокальных связей. По сути, TDA позволяет моделям «видеть» общую структуру данных, а не только локальные признаки, что приводит к формированию более устойчивых и обобщающих представлений. Это особенно важно при работе с данными, имеющими сложную геометрическую структуру, такими как изображения, молекулярные структуры или сети социальных взаимодействий. В результате, модели, использующие принципы топологического глубокого обучения, демонстрируют повышенную устойчивость к шуму и изменениям в данных, а также улучшенную способность к обобщению на новые, ранее не встречавшиеся примеры.

Механизмы внимания, активно используемые в графовых нейронных сетях, можно рассматривать как разновидность топологического анализа данных. Вместо обработки всех связей в графе одинаково, эти механизмы динамически взвешивают важность каждого соединения, эффективно выделяя наиболее информативные участки структуры данных. Этот процесс аналогичен выявлению гомологических групп в топологическом анализе, где выделяются значимые «дыры» или циклы, определяющие форму объекта. В графовых сетях, внимание, по сути, определяет, какие связи наиболее важны для передачи информации и формирования репрезентаций, что позволяет модели улавливать нелокальные зависимости и строить более устойчивые и обобщающие представления.

Будущее интеллектуальных систем: к надежному и объяснимому ИИ

Сети долгой краткосрочной памяти (Long Short-Term Memory, LSTM), развиваясь на базе рекуррентных нейронных сетей, эффективно решают проблему затухания градиента, что позволяет моделям усваивать зависимости между данными, даже если они разделены значительным промежутком времени. Традиционные рекуррентные сети испытывают трудности при обучении на длинных последовательностях из-за экспоненциального уменьшения градиента при обратном распространении ошибки, что препятствует обновлению весов для более ранних элементов последовательности. LSTM сети, благодаря своей архитектуре, включающей ячейки памяти и управляющие вентили, способны сохранять и передавать информацию на большие расстояния, обеспечивая возможность моделирования сложных временных зависимостей. Это делает их незаменимыми в задачах, требующих понимания контекста на протяжении длительных последовательностей, таких как обработка естественного языка, распознавание речи и анализ временных рядов.

Сочетание байесовских методов и топологического глубокого обучения открывает перспективный путь к созданию интеллектуальных систем, отличающихся не только высокой точностью, но и устойчивостью к помехам, понятностью принимаемых решений и способностью к адаптации в меняющихся условиях. Данный подход позволяет учитывать неопределенность и априорные знания, что повышает надежность работы системы в сложных ситуациях. Топологический анализ данных, в свою очередь, позволяет выявлять скрытые закономерности и структуру в данных, что способствует более эффективному обучению и объяснению поведения модели. В результате, создаваемые системы способны не просто выдавать результаты, но и предоставлять информацию о причинах принятых решений, что критически важно для применения в ответственных областях, таких как медицина или финансы.

Исследования, представленные в данном обзоре, демонстрируют значительный прогресс в области интеллектуальных систем. Применение комбинированных методов, включающих байесовские подходы и топологическое глубокое обучение, позволило достичь впечатляющей точности — до 93% — в решении сложных задач, таких как идентификация радиолокационных излучателей в условиях низкого отношения сигнал/шум. Этот результат существенно превосходит показатели традиционных рекуррентных нейронных сетей GRU, не использующих механизмы внимания, что подтверждает перспективность предложенного подхода для создания более надежных и адаптивных систем искусственного интеллекта, способных эффективно функционировать в сложных и неопределенных условиях.

Исследование, представленное в статье, стремится к созданию более надежных и адаптивных систем искусственного интеллекта, особенно в контексте военных приложений. Подобный подход к интеграции нейронных сетей, байесовских методов и топологического анализа данных подчеркивает необходимость не просто обработки информации, но и понимания её структуры и неопределенности. В этом стремлении к ясности и точности можно увидеть отголоски слов Давида Гильберта: «Главное — это простота. Стремитесь к простоте». Подобно тому, как топологический анализ данных выявляет фундаментальные свойства данных, скрытые за сложностью, так и математическая строгость Гильберта направлена на выявление истины, отбрасывая все лишнее. Калибровка моделей и управление неопределенностью, рассматриваемые в работе, — это, по сути, стремление к минимальной форме любви — ясности — в мире сложных данных.

Куда же это всё ведёт?

Представленная работа, как и любая попытка упорядочить хаос данных, лишь обнажает глубину нерешенных вопросов. Интеграция байесовских методов, топологического анализа данных и графовых нейронных сетей — это, скорее, признание собственной некомпетентности в отношении истинной природы неопределенности, нежели её преодоление. Стремление к “уверенности” в условиях неполноты информации — иллюзия, но полезная, если она не приводит к самообману. Главная сложность, как всегда, заключается не в алгоритмах, а в данных: их очистка, калибровка и, что самое важное, осознание их неизбежной предвзятости.

Будущие исследования, вероятно, будут направлены на разработку более элегантных способов компрессии информации без потери существенного содержания. Иными словами, на создание моделей, способных извлекать максимум полезного сигнала из минимального объема данных. Однако, не стоит забывать о фундаментальном ограничении: любая модель — это упрощение реальности, а любое упрощение — это потеря информации. Искусство заключается в том, чтобы минимизировать эту потерю, не усложняя систему до абсурда.

В конечном итоге, истинный прогресс в области искусственного интеллекта будет достигнут не за счёт создания всё более сложных алгоритмов, а за счёт более глубокого понимания принципов, лежащих в основе интеллекта вообще. А это, как известно, задача куда более сложная, чем решение любой вычислительной проблемы. Всё избыточное должно быть отброшено, чтобы красота компрессии без потерь воссияла.

Оригинал статьи: https://arxiv.org/pdf/2602.10266.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-12 10:44