Нейронные сети и тайна активности мозга: новый взгляд

Автор: Денис Аветисян

Исследователи показали, как графовые нейронные сети способны расшифровать внутреннюю структуру и динамику нейронных ансамблей по данным об их активности.

🐢

Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.

Телеграм канал

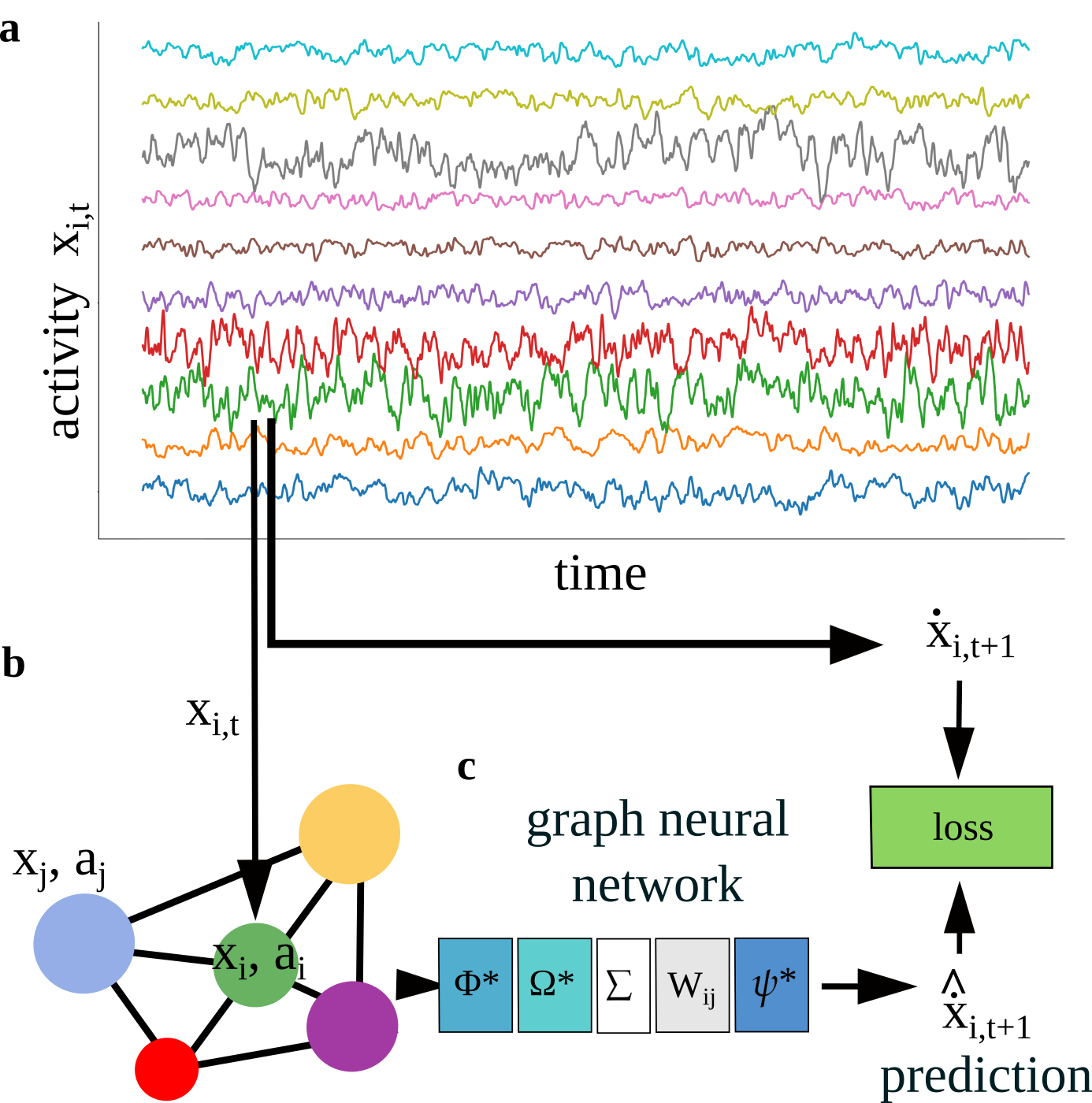
Моделирование нейронной сети преобразует временную активность нейронов в плотный граф, обрабатываемый графовой нейронной сетью, где каждый нейрон, получая сигналы от связанных нейронов, взвешивает их матрицей <span class="katex-eq" data-katex-display="false">\boldsymbol{W}</span>, преобразует функцией <span class="katex-eq" data-katex-display="false">\psi^{\<i>}</span> и обновляет свою активность посредством функций <span class="katex-eq" data-katex-display="false">\phi^{\</i>}</span> и <span class="katex-eq" data-katex-display="false">\Omega^{\*}</span>, используя, помимо наблюдаемой активности <span class="katex-eq" data-katex-display="false">x_i</span>, обучаемые латентные векторы <span class="katex-eq" data-katex-display="false">\boldsymbol{a}_i</span>. — Моделирование нейронной сети преобразует временную активность нейронов в плотный граф, обрабатываемый графовой нейронной сетью, где каждый нейрон, получая сигналы от связанных нейронов, взвешивает их матрицей $\boldsymbol{W}$ , преобразует функцией $\psi^{\<i>}$ и обновляет свою активность посредством функций $\phi^{\</i>}$ и $\Omega^{\*}$ , используя, помимо наблюдаемой активности $x_i$ , обучаемые латентные векторы $\boldsymbol{a}_i$ .

Графовые нейронные сети позволяют восстановить связи, функциональные характеристики и даже внешние стимулы, влияющие на активность смоделированных нейронных ансамблей.

Понимание принципов работы сложных нейронных ансамблей затруднено из-за высокой размерности и нелинейности динамических процессов. В работе ‘Graph neural networks uncover structure and functions underlying the activity of simulated neural assemblies’ представлен подход, использующий графовые нейронные сети для анализа активности смоделированных нейронных ансамблей. Показано, что данный метод позволяет одновременно восстанавливать матрицу связей, типы нейронов, функциональные характеристики и даже скрытые внешние стимулы, действующие на систему. Способны ли подобные модели стать основой для более глубокого понимания организации и функционирования реальных нейронных сетей мозга?

Порядок из Локальных Правил: Преодолевая Упрощения в Моделях Нейронных Сетей

Традиционные подходы в вычислительной нейронауке зачастую упрощают взаимодействие нейронов, что приводит к потере важной информации о динамике нейронных сетей. Модели, основанные на усредненных параметрах и упрощенных связях, могут упускать из виду критические детали, такие как временные задержки, нелинейные эффекты и гетерогенность нейронных популяций. Эти упрощения, хотя и позволяют проводить масштабные симуляции, могут искажать реальные процессы обработки информации в мозге. В результате, возникают расхождения между предсказаниями моделей и экспериментальными данными, что затрудняет понимание сложных когнитивных функций и механизмов нейронных расстройств. Учитывая, что даже незначительные изменения в синаптической активности могут существенно повлиять на поведение сети, необходимы более детализированные и реалистичные модели, способные отразить всю сложность нейронных взаимодействий.

Для точного моделирования работы нейронных ансамблей необходимо учитывать не только общую структуру связей, но и тонкости индивидуальных характеристик каждого нейрона. Традиционные подходы часто упрощают взаимодействие, рассматривая нейроны как однородные единицы, что приводит к потере информации о динамике сети. Более реалистичные модели стремятся к учету разнообразия морфологии, экспрессии генов и электрофизиологических свойств каждого нейрона, а также к детализации синаптических связей, включая их пластичность и пространственное распределение. Такой подход позволяет исследовать, как индивидуальные особенности нейронов влияют на функционирование ансамбля в целом, и как эти различия могут быть ключевыми для реализации сложных когнитивных функций. Использование методов, учитывающих нюансы связности и индивидуальные свойства, открывает новые возможности для понимания механизмов обучения, памяти и обработки информации в мозге.

Существующие вычислительные методы часто сталкиваются с трудностями при одновременном учете как высокой детализации биологических моделей нейронов, так и необходимости проведения масштабных симуляций. Традиционные подходы, стремящиеся к упрощению для повышения вычислительной эффективности, нередко теряют критически важные аспекты нейронной динамики, что ограничивает их применимость к моделированию сложных нейронных ансамблей. В то же время, модели, точно воспроизводящие биофизические свойства отдельных нейронов, оказываются непомерно затратными с точки зрения вычислительных ресурсов, что делает невозможным моделирование крупномасштабных нейронных сетей и изучение их функционирования в реальном времени. Разработка новых алгоритмов и вычислительных стратегий, позволяющих преодолеть этот разрыв между детализацией и масштабируемостью, является ключевой задачей современной вычислительной нейронауки, открывающей путь к более реалистичному и информативному моделированию работы мозга.

Обученная на симуляции из 1000 плотно связанных нейронов GNN-модель успешно восстанавливает активность нейронов во времени (графики активности 25 нейронов представлены на панелях a и c), демонстрируя высокую корреляцию между истинными и предсказанными значениями активности для всех 1000 нейронов (панели b и d).

Графовые Нейронные Сети: Возникающие Паттерны в Структуре Связей

Для моделирования взаимосвязей внутри нейронной сборки используется графовая нейронная сеть (ГНС). В данной модели отдельные нейроны представлены как узлы графа, а синаптические связи между ними — как ребра. Такое представление позволяет ГНС оперировать структурой связей непосредственно, рассматривая нейронную сборку как граф, где $N$ узлов соответствуют нейронам, а каждое ребро $(i, j)[latex] указывает на наличие синаптической связи от нейрона [latex]i$ к нейрону $j$ . Использование ГНС позволяет эффективно анализировать и моделировать динамику, определяемую паттерном связности нейронной сети.

Графовая нейронная сеть (ГНС) позволяет определить ключевые характеристики нейронной сети, такие как тип нейрона и правило обновления, непосредственно на основе матрицы связей. Анализ матрицы связей, отражающей паттерны коннективности между нейронами, предоставляет информацию, необходимую для вывода этих свойств. ГНС использует структуру графа, представленного матрицей связей, для определения функционального состояния нейронной сети без необходимости явного задания параметров отдельных нейронов или связей. Этот подход позволяет эффективно моделировать и понимать динамику сложных нейронных ансамблей, используя только информацию о паттернах коннективности.

Использование векторного представления латентного пространства для описания свойств нейронов позволяет эффективно моделировать гетерогенность нейронных ансамблей. Вместо явного кодирования каждого параметра каждого нейрона, мы отображаем свойства нейронов в пространство меньшей размерности - $ℝⁿ$ , где $n << d$ (где $d$ - количество параметров, описывающих каждый нейрон). Это значительно снижает вычислительную сложность и объем памяти, необходимые для представления больших нейронных сетей, сохраняя при этом возможность захвата существенных различий между нейронами. Такой подход особенно важен при моделировании крупных ансамблей, где прямой учет всех параметров каждого нейрона становится непрактичным.

Обучение графовой нейронной сети (GNN) с фиксированными латентными векторами для 1000 плотно связанных нейронов позволило воссоздать истинные связи и функции обновления (<span class="katex-eq" data-katex-display="false"> \phi^{\<i>}(\boldsymbol{a},x) </span> и <span class="katex-eq" data-katex-display="false"> \psi^{\</i>}(x) </span>), несмотря на предположение об идентичности всех нейронов, что подтверждается сравнением истинных и полученных связей и функций (на примере <span class="katex-eq" data-katex-display="false"> g_{i}=10 </span>). — Обучение графовой нейронной сети (GNN) с фиксированными латентными векторами для 1000 плотно связанных нейронов позволило воссоздать истинные связи и функции обновления ( $\phi^{\<i>}(\boldsymbol{a},x)$ и $\psi^{\</i>}(x)$ ), несмотря на предположение об идентичности всех нейронов, что подтверждается сравнением истинных и полученных связей и функций (на примере $g_{i}=10$ ).

От Симуляции к Выводу: Предсказательная Сила Возникающих Моделей

Для создания реалистичных сценариев и исследования динамики нейронных ансамблей используется моделирование. В процессе симуляции нейронный ансамбль подвергается воздействию разнообразных внешних стимулов, варьирующихся по интенсивности и продолжительности. Этот подход позволяет генерировать широкий спектр входных данных, имитирующих реальные условия, и исследовать реакцию ансамбля на различные типы стимуляции. Разнообразие внешних стимулов критически важно для оценки устойчивости и обобщающей способности модели, а также для выявления ключевых факторов, влияющих на активность нейронного ансамбля.

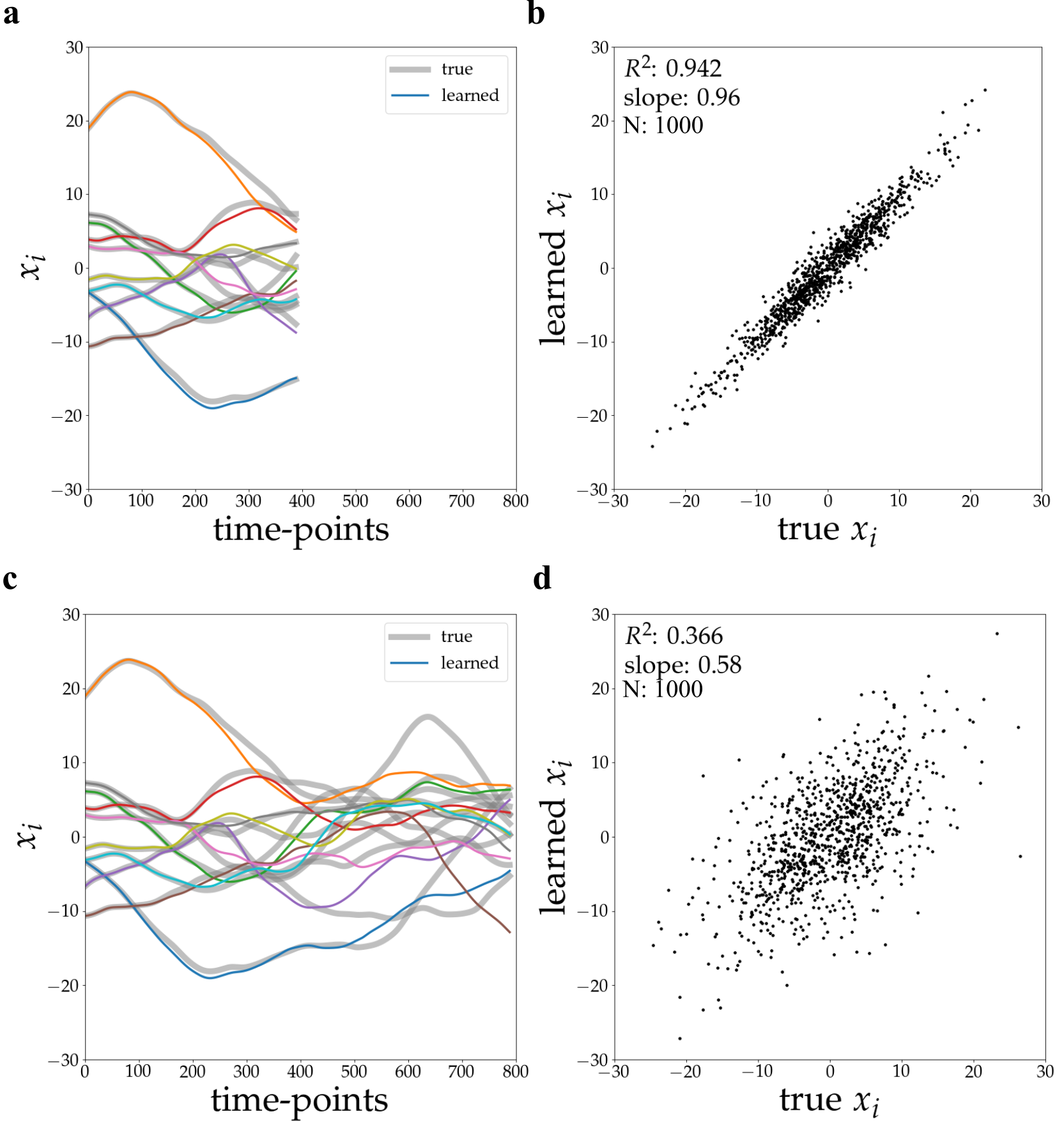
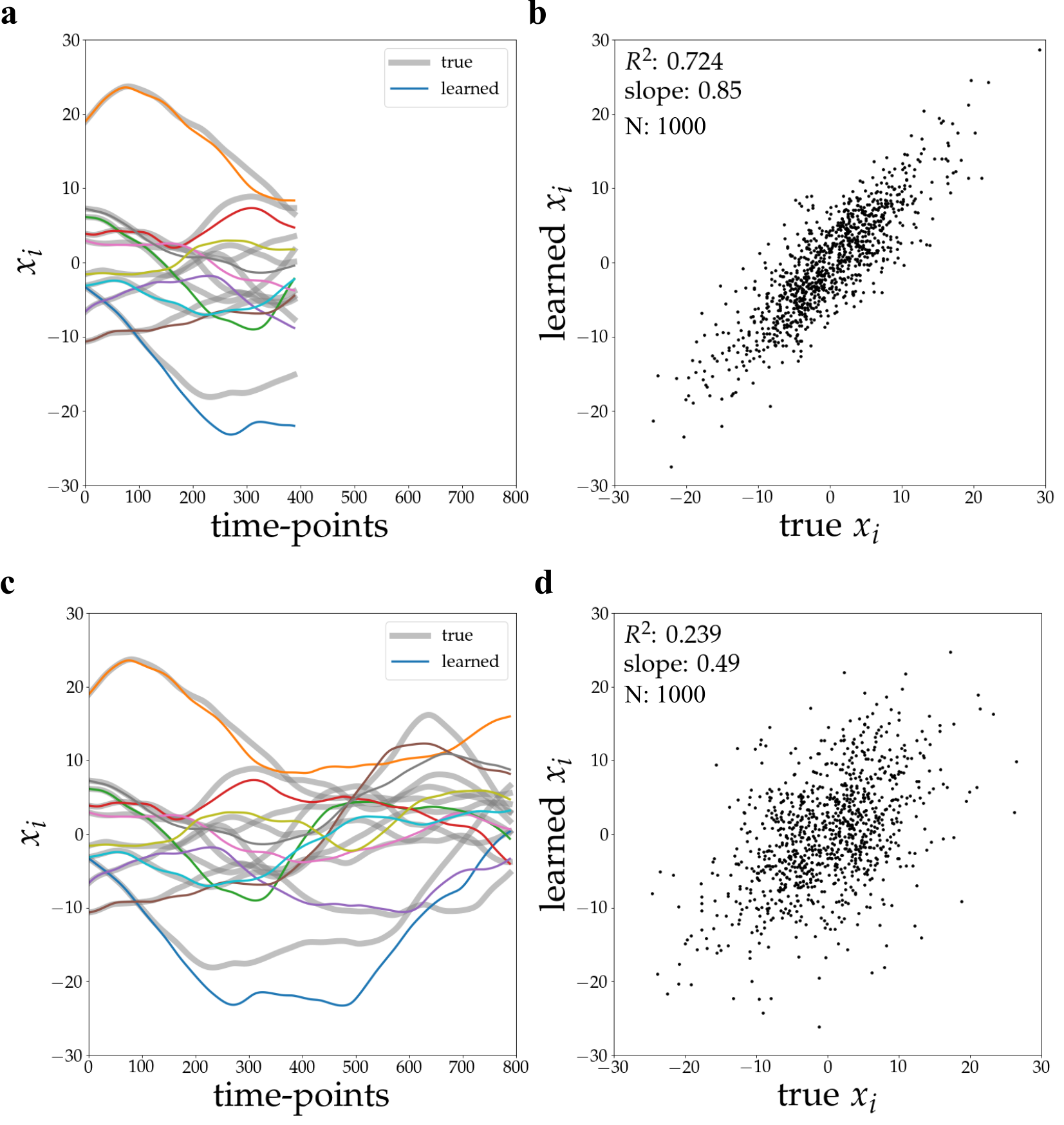
Метод развертывания (Rollout Inference) использует обученную графовую нейронную сеть (GNN) для прогнозирования динамики нейронной сети в ответ на внешние стимулы. Данный подход демонстрирует способность прогнозировать активность сети во временном масштабе, достигая коэффициента детерминации $R^2$ равного 0.996 в течение 800 временных шагов. Высокое значение $R^2$ указывает на высокую степень соответствия между прогнозируемой и фактической активностью сети, подтверждая эффективность метода в предсказании временной динамики.

Для повышения точности предсказаний и предотвращения переобучения модели, применяются методы регуляризации. Эти методы ограничивают сложность графовой нейронной сети (GNN), снижая ее чувствительность к шуму в данных и позволяя ей лучше обобщать полученные знания на новые, ранее не встречавшиеся стимулы. Регуляризация достигается за счет добавления штрафных членов к функции потерь, которые наказывают за излишне сложные параметры модели. Это способствует созданию более устойчивой и надежной системы предсказаний, способной эффективно работать с разнообразными входными данными и сохранять высокую точность прогнозирования во времени.

Анализ результатов работы GNN-модели, обученной на гипотезе об идентичности всех нейронов, показывает, что к моменту времени 200 и 800 модель способна воссоздать активность нейронов, что подтверждается сравнением 25 обученных траекторий активности (a, c) с фактическими траекториями (светло-серым цветом) и сопоставлением значений активности 1000 нейронов (b, d).

Раскрытие Причинных Связей и Расширение Понимания: От Локальных Правил к Глобальному Поведению

Исследование позволило установить причинно-следственные связи внутри нейронных ансамблей, раскрывая, каким образом конкретные соединения влияют на активность сети. Применяя методы причинного вывода, ученые смогли не просто наблюдать корреляции между различными участками нейронной сети, но и определить, какие связи являются ключевыми для формирования определенных паттернов активности. Этот подход позволяет понять, как изменение силы или наличия конкретного соединения может приводить к изменению поведения всей нейронной сети, что открывает новые возможности для изучения механизмов обучения, памяти и принятия решений. Выявление этих причинно-следственных связей имеет решающее значение для разработки более точных моделей работы мозга и создания эффективных стратегий нейромодуляции.

Для углубленного анализа динамики нейронных ансамблей была применена методика символьной регрессии, позволяющая вывести аналитические выражения, описывающие функции переноса. Этот подход, в отличие от традиционных численных методов, позволяет получить компактные математические формулы, отражающие взаимосвязь между входными и выходными сигналами нейронной сети. Полученные функции переноса $F(x)$ позволяют не только понимать, как конкретные связи влияют на активность сети, но и предсказывать её поведение в различных условиях, а также проводить более точный анализ стабильности и чувствительности системы. Использование символьной регрессии открывает новые возможности для моделирования сложных нейронных процессов и выявления ключевых механизмов, определяющих функционирование мозга.

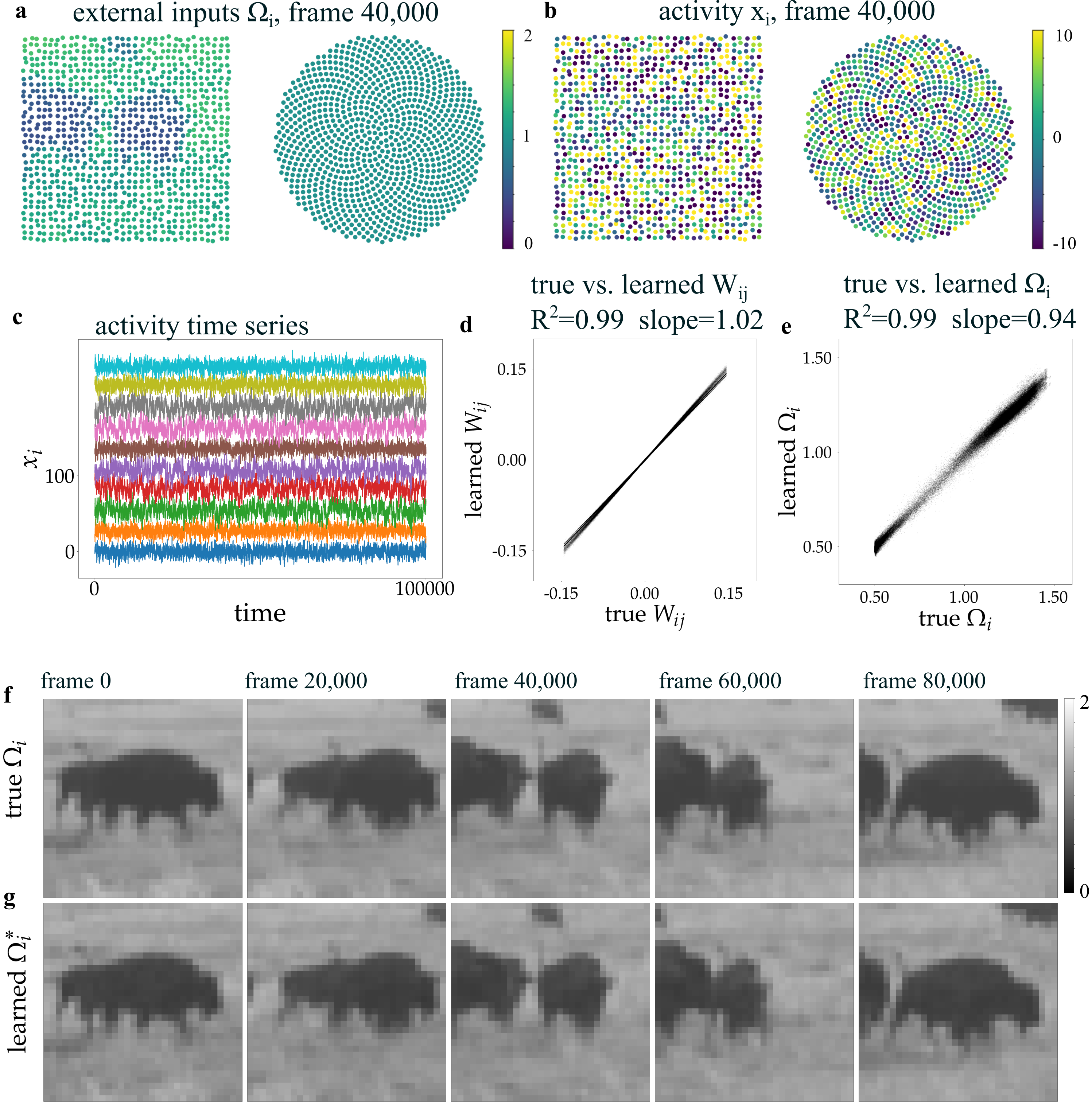
Использование многослойного персептрона, основанного на координатах (Coordinate-Based MLP), позволило эффективно смоделировать влияние пространственных внешних стимулов на активность нейронной сети. Данный подход демонстрирует исключительную точность: реконструкция матрицы связности достигает коэффициента детерминации $R^2 = 1.00$ , что свидетельствует о полном соответствии модели и данных. Более того, классификация типов нейронов осуществляется с абсолютной точностью - 1.00, указывая на способность модели к четкому различению и идентификации различных нейронных популяций. Такая высокая производительность подчеркивает потенциал координатно-зависимого подхода в понимании и моделировании влияния пространственной информации на нейронные процессы.

Обучение нейронной сети из 2048 плотно связанных нейронов с различными функциями обновления и передачи, под воздействием внешних входных сигналов <span class="katex-eq" data-katex-display="false">\Omega_{i}(t)</span>, позволило успешно восстановить как матрицу связей <span class="katex-eq" data-katex-display="false">\boldsymbol{W}_{ij}</span>, так и временную зависимость внешнего поля <span class="katex-eq" data-katex-display="false">\Omega_{i}(t)</span>, что подтверждается сравнением истинных и обученных значений на временных рядах, состоящих из <span class="katex-eq" data-katex-display="false">10^5</span> точек. — Обучение нейронной сети из 2048 плотно связанных нейронов с различными функциями обновления и передачи, под воздействием внешних входных сигналов $\Omega_{i}(t)$ , позволило успешно восстановить как матрицу связей $\boldsymbol{W}_{ij}$ , так и временную зависимость внешнего поля $\Omega_{i}(t)$ , что подтверждается сравнением истинных и обученных значений на временных рядах, состоящих из $10^5$ точек.

Исследование демонстрирует, что порядок в сложных нейронных ансамблях возникает не из централизованного управления, а из локальных взаимодействий между элементами. Подобно лесу, развивающемуся без лесника, но с правилами света и воды, нейронные сети формируют свою структуру и функциональность на основе внутренних связей и внешних стимулов. Как заметил Джон Стюарт Милль: «Свобода, определяющаяся отсутствием принуждения, является необходимым условием интеллектуального, практического и морального прогресса». В данном исследовании, способность графовых нейронных сетей восстанавливать структуру и динамику ансамблей из данных об активности, подтверждает, что понимание локальных правил взаимодействия является ключом к постижению сложного порядка, возникающего в динамических системах.

Что дальше?

Представленные результаты демонстрируют, что из кажущегося хаоса динамических систем, таких как нейронные ансамбли, возможно извлечение упорядоченных структур посредством применения графовых нейронных сетей. Однако, стоит признать, что восстановление “истинной” организации - задача, обреченная на неполноту. Любая модель, даже самая сложная, - это лишь приближение, фильтр, накладывающий определенные ограничения на бесконечное разнообразие реальности. Ограничения, в свою очередь, - не препятствие, а стимул к изобретательности.

Наиболее перспективным представляется отказ от поиска единой “правильной” модели. Вместо этого, целесообразно исследовать пространство возможных интерпретаций, оценивая их пригодность не по критерию соответствия исходным данным, а по способности генерировать новые, предсказуемые и наблюдаемые явления. Интересно, как подобные подходы могут быть расширены для анализа не только активности, но и морфологических особенностей нейронных ансамблей, создавая более целостную картину их функционирования.

В конечном итоге, важно помнить: порядок не нуждается в архитекторе - он возникает из локальных правил. Контроль - иллюзия, влияние - реально. Попытки “управлять” сложными системами, вероятно, менее эффективны, чем создание условий, способствующих их самоорганизации и адаптации.

Оригинал статьи: https://arxiv.org/pdf/2602.13325.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-17 15:04