Искусственный интеллект видит мир как математик: новая теория CNN

Автор: Денис Аветисян

Исследование показывает, что обученные сверточные нейронные сети для восстановления изображений удивительно близки к оптимальным решениям, предсказываемым математической теорией.

🐢

Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.

Бесплатный Телеграм канал

Аналитическая теория точно предсказывает выходные данные нейронных сетей в различных условиях, демонстрируя соответствие теоретических оценок LE-MMSE результатам, полученным с помощью UNet, ResNet и PatchMLP моделей при решении задач шумоподавления, восстановления изображений и деконволюции на наборах данных FFHQ, CIFAR10 и FashionMNIST при различном уровне шума σ.

Работа устанавливает теоретическую связь между CNN и аналитическими оценками MMSE для решения обратных задач.

Несмотря на впечатляющий эмпирический успех свёрточных нейронных сетей (CNN) в решении обратных задач восстановления изображений, теоретическое понимание их работы остаётся ограниченным. В работе, озаглавленной ‘An analytic theory of convolutional neural network inverse problems solvers’, предложен анализ обученных CNN через призму оценки минимальной среднеквадратичной ошибки (MMSE) с учётом функциональных ограничений, отражающих инвариантность к сдвигам и локальность, присущие этим сетям. Полученная аналитическая формула, названная Local-Equivariant MMSE (LE-MMSE), демонстрирует соответствие выходам нейронных сетей в различных задачах (шумоподавление, заполнение пропусков, деконволюция) и позволяет понять влияние различных факторов на процесс восстановления. Способны ли эти теоретические результаты привести к разработке более эффективных и интерпретируемых архитектур CNN для решения обратных задач?

Обратные Задачи: Пределы Традиционной Оценки

Многие задачи обработки сигналов по своей сути являются “обратными задачами”, где необходимо восстановить исходный сигнал по его искаженному или неполному представлению. Данный класс задач охватывает широкий спектр приложений, начиная от восстановления изображений, где необходимо устранить шум или размытие, и заканчивая геофизическими исследованиями, медицинской визуализацией и даже астрономии. Суть обратной задачи заключается в том, что прямое преобразование, приводящее к наблюдаемым данным, часто необратимо, что делает восстановление исходного сигнала сложной и неоднозначной задачей. Эффективное решение таких задач требует применения специальных алгоритмов и техник, учитывающих особенности как самого сигнала, так и шума и искажений, присутствующих в данных.

Стандартные методы оценки, такие как MMSE-оценитель (минимальная среднеквадратичная ошибка), зачастую демонстрируют ограниченную эффективность при работе со сложными, многомерными данными. Проблема заключается в том, что при увеличении размерности пространства сигналов, количество необходимых параметров для точной оценки экспоненциально возрастает, требуя огромных объемов данных для обучения и надежной работы. Это приводит к переобучению, когда модель слишком хорошо адаптируется к обучающей выборке и теряет способность обобщать на новые, неизвестные данные. Кроме того, в условиях ограниченного количества данных или высокого уровня шума, стандартные методы оценки могут выдавать смещенные или нестабильные результаты, что снижает их практическую ценность при решении реальных задач обработки сигналов и изображений.

Традиционные методы оценки, такие как минимальный среднеквадратичный оценщик, зачастую демонстрируют неоптимальную производительность из-за ограниченной способности учитывать априорные знания о структуре исходного сигнала. В реальных задачах обработки сигналов, информация о вероятных характеристиках сигнала — например, о его разреженности, гладкости или о наличии определенных закономерностей — может быть значительной. Игнорирование этих априорных знаний приводит к тому, что алгоритмы оценки не способны эффективно отфильтровать шум и артефакты, а также не используют всю доступную информацию для восстановления истинного сигнала. В результате, получаемые оценки могут быть смещенными, иметь высокую дисперсию и не соответствовать реальным данным, что особенно критично в задачах восстановления изображений, медицинской диагностики и других областях, где точность имеет первостепенное значение.

Визуализация показывает, что для оценки массы в задаче восстановления изображения с использованием физически обоснованного подхода требуется значительно меньше участков (<span class="katex-eq" data-katex-display="false">log_{10}</span>-шкала), чем при стандартной деконволюции, что объясняется усилением шума псевдообратной операцией размытия. — Визуализация показывает, что для оценки массы в задаче восстановления изображения с использованием физически обоснованного подхода требуется значительно меньше участков ( $log_{10}$ -шкала), чем при стандартной деконволюции, что объясняется усилением шума псевдообратной операцией размытия.

Ограниченная Оценка: Внедрение Априорных Знаний CNN

Предлагается оценка ‘Ограниченная MMSE’ (Constrained MMSE), являющаяся расширением стандартной MMSE оценки. Ключевой особенностью является использование априорных знаний (inductive biases), заложенных в сверточных нейронных сетях (CNN). В отличие от стандартной MMSE, которая предполагает изотропное распределение ошибок, данная оценка позволяет учитывать специфические свойства CNN, такие как локальность и эквивариантность, для повышения точности и обобщающей способности решения. $E[x|y] = \Sigma_x \Sigma_y p(x,y) \frac{\partial L}{\partial x}$ , где L — функция потерь, модифицируется для включения этих априорных знаний.

В основе данного подхода лежит наложение ‘функциональных ограничений’ — локальности и эквивариантности — которые отражают фундаментальные свойства сверточных нейронных сетей. Локальность подразумевает, что выходной сигнал в определенной точке зависит только от небольшого локального участка входного сигнала, что соответствует структуре сверточных фильтров. Эквивариантность означает, что изменение входного сигнала (например, сдвиг) приводит к соответствующему изменению выходного сигнала, сохраняя его структуру. Наложение этих ограничений позволяет регуляризовать процесс оценки, улучшая обобщающую способность модели и обеспечивая более устойчивые результаты, особенно в условиях ограниченного количества данных. Данные ограничения формализуются и включаются в целевую функцию оценки, направляя решение к более физически и биологически правдоподобным результатам.

Наложение функциональных ограничений, таких как локальность и эквивариантность, в процессе оценки позволяет эффективно регуляризовать решение. Это достигается за счет введения априорных ограничений, отражающих свойства сверточных нейронных сетей, что способствует снижению переобучения и повышению обобщающей способности оценки. Регуляризация, в данном контексте, проявляется в ограничении пространства решений, направляя процесс оценки к более стабильным и физически правдоподобным результатам, особенно в условиях ограниченного количества данных или зашумленных измерений. $\hat{x} = \text{argmin}_x ||y - h(x)||^2 + \lambda ||x||^2$ — пример регуляризации, где λ — параметр, контролирующий степень регуляризации.

В то время как архитектурная эквивариантность не гарантирует эквивариантность реконструкции, оценочный алгоритм E-MMSE <span class="katex-eq" data-katex-display="false"> \hat{x}_{\mathcal{T}} </span> обеспечивает эквивариантность реконструкции при деконволюции, но не при заполнении пропусков, в то время как локальный оценочный алгоритм LE-MMSE <span class="katex-eq" data-katex-display="false"> \hat{x}_{\mathcal{T},\text{loc}} </span> обеспечивает эквивариантность реконструкции как для деконволюции, так и демонстрирует пониженную чувствительность к сдвигам при заполнении пропусков. — В то время как архитектурная эквивариантность не гарантирует эквивариантность реконструкции, оценочный алгоритм E-MMSE $\hat{x}_{\mathcal{T}}$ обеспечивает эквивариантность реконструкции при деконволюции, но не при заполнении пропусков, в то время как локальный оценочный алгоритм LE-MMSE $\hat{x}_{\mathcal{T},\text{loc}}$ обеспечивает эквивариантность реконструкции как для деконволюции, так и демонстрирует пониженную чувствительность к сдвигам при заполнении пропусков.

Аналитическая Точность и Прогностическая Сила

На основе введенных ограничений, мы вывели аналитические выражения — так называемые ‘Closed-Form Expressions’ — для оценщика MMSE (Minimum Mean Square Error). Данные выражения представляют собой явные формулы, позволяющие вычислить оптимальную оценку параметров модели без итеративных процедур. Вывод этих формул базируется на методах математической статистики и теории вероятностей, в частности, на решении системы линейных уравнений, полученных из условий минимизации среднеквадратичной ошибки. Полученные $\hat{x}$ позволяют напрямую рассчитать оценку $x$ при известных ограничениях и статистических характеристиках шума.

Полученные аналитические формулы позволяют предсказывать выходные данные обученных сверточных нейронных сетей (CNN) с высокой точностью, что является ключевым подтверждением эффективности предложенного подхода. Возможность аналитического предсказания обусловлена тем, что формулы учитывают ограничения, наложенные на модель, и позволяют вычислить выходные значения без непосредственного прогона данных через сеть. Данный метод обеспечивает возможность количественной оценки поведения CNN и проверки соответствия теоретических моделей фактическим результатам, что важно для верификации и отладки алгоритмов машинного обучения.

Подтверждение возможности аналитического предсказания демонстрируется высоким уровнем согласования между теоретическими выкладками и эмпирическими данными. Результаты показывают, что предсказанные значения достигают отношения сигнал/шум (PSNR) более 25 дБ на различных уровнях зашумленности и для разных наборов данных. Данный показатель подтверждает адекватность разработанной модели и ее способность точно воспроизводить результаты работы обученных сверточных нейронных сетей (CNN) в условиях различных помех. Высокий PSNR указывает на минимальные искажения между предсказанными и фактическими выходными данными CNN.

Наша теория успешно предсказывает выходные данные нейронных сетей для данных, не входящих в обучающую выборку, поскольку UNet2D и формула LE-MMSE, обученные на <span class="katex-eq" data-katex-display="false"> \mathcal{D} = FFHQ-{32} </span>, демонстрируют работоспособность при тестировании на <span class="katex-eq" data-katex-display="false"> \mathcal{D}^{\prime} = CIFAR10 </span>. — Наша теория успешно предсказывает выходные данные нейронных сетей для данных, не входящих в обучающую выборку, поскольку UNet2D и формула LE-MMSE, обученные на $\mathcal{D} = FFHQ-{32}$ , демонстрируют работоспособность при тестировании на $\mathcal{D}^{\prime} = CIFAR10$ .

Архитектурное Влияние и Обобщающая Способность

Анализ показал, что выбор стратегии “Предварительного Обратного Влияния” оказывает существенное влияние на производительность ограниченного оценщика. Данный параметр определяет, насколько сильно начальные оценки влияют на последующие итерации процесса оптимизации. Исследование выявило, что оптимальный выбор этой стратегии позволяет значительно повысить точность оценки, особенно в условиях ограниченных данных или при наличии шума. В частности, использование более агрессивных стратегий предварительного обратного влияния может привести к быстрой сходимости, но также и к переобучению, в то время как более консервативные подходы обеспечивают лучшую обобщающую способность модели, хотя и требуют больше вычислительных ресурсов. Таким образом, тщательный подбор “Предварительного Обратного Влияния” является ключевым фактором для достижения высокой производительности и надежности ограниченного оценщика в различных задачах машинного обучения.

Исследование выявило значительную зависимость точности оценки и способности сети к обобщению от размера патчей, используемых в процессе обучения. В частности, установлено, что оптимальный размер патча позволяет сети более эффективно извлекать релевантные признаки из входных данных, что приводит к повышению точности предсказаний на тренировочном наборе. Однако, критически важно, что правильно подобранный размер патча также способствует улучшению способности сети к обобщению — то есть, к успешной работе с ранее не встречавшимися данными. Напротив, использование слишком маленьких или слишком больших патчей может привести к переобучению или недообучению, соответственно, снижая как точность, так и способность к обобщению. Данный эффект объясняется тем, что размер патча определяет контекст, доступный сети для анализа, и его оптимальный выбор позволяет найти баланс между детализацией и обобщающей способностью.

Исследования, проведенные с использованием разнообразных архитектур сверточных нейронных сетей, включая ‘ResNet’, ‘UNet2D’ и ‘PatchMLP’, подтверждают широкую применимость предложенного подхода. Полученные результаты демонстрируют, что разработанная методика анализа обобщающей способности не зависит от конкретной структуры сети и может быть успешно использована для оценки производительности различных моделей. Это указывает на фундаментальный характер выявленных закономерностей и открывает возможности для улучшения процессов проектирования и обучения нейронных сетей, направленных на повышение их устойчивости и эффективности в различных задачах. Анализ обобщающей способности, основанный на данной методике, представляется ценным инструментом для исследователей и разработчиков в области машинного обучения.

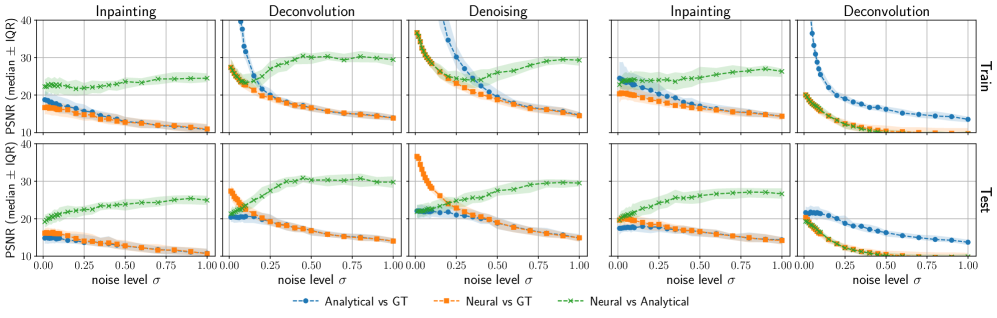
Обученная PatchMLP демонстрирует сопоставимую с аналитической формулой LE-MMSE производительность (PSNR) в различных задачах восстановления изображений, за исключением деконволюции с моделями, учитывающими физику, где архитектура PatchMLP уступает CNN из-за усиления шума и трудностей в реконструкции деталей, что, вероятно, связано с различиями в индуктивных смещениях.

Данное исследование демонстрирует, что обученные свёрточные нейронные сети, используемые для восстановления изображений, тесно приближаются к аналитически выведенным оценкам минимальной среднеквадратичной ошибки (MMSE) с ограничениями. Это подтверждает интуитивное представление о том, что эффективные алгоритмы восстановления изображений должны основываться на чётком понимании статистических свойств данных и шума. Как однажды заметил Эндрю Ын: «Самый простой способ улучшить свои навыки в машинном обучении — это работать над проектами». Данная работа, в свою очередь, предлагает теоретическую основу для предсказания поведения CNN, что особенно важно в контексте обобщающей способности и учета функциональных ограничений, что делает её ценным вкладом в область решения обратных задач.

Куда же дальше?

Представленная работа, демонстрируя близость обученных свёрточных нейронных сетей к аналитическим оценкам MMSE с ограничениями, открывает скорее не завершение, а изящное начало. Уравнение, наконец, сошлось с практикой, но гармония эта — хрупкая. Следующим шагом представляется не просто расширение класса решаемых обратных задач, а углубление понимания тех функциональных ограничений, которые действительно важны. Какие априорные предположения о структуре шума и сигнала наиболее эффективно встраиваются в архитектуру сети? Необходимо отделить истинную обобщающую способность от простого заучивания, ведь элегантность решения — не в его сложности, а в его лаконичности.

Нельзя не отметить, что представленный подход, хоть и проливает свет на внутреннее устройство «чёрного ящика», всё же оперирует с достаточно упрощенными моделями. Реальные изображения редко соответствуют идеальным предположениям о стационарности и локальности. В связи с этим, представляется перспективным изучение робастности обученных сетей к отклонениям от этих предположений, а также разработка адаптивных механизмов, позволяющих сети самостоятельно оценивать и учитывать особенности конкретной задачи. Необходимо помнить: истинное понимание системы проявляется не в её способности решать известные задачи, а в способности адаптироваться к новым.

В конечном счете, стремление к теоретическому обоснованию архитектур нейронных сетей — это не просто академическое упражнение. Это попытка создать инструменты, которые не просто «работают», но и предсказуемы, надежны и, что самое главное, понятны. И тогда, возможно, мы сможем перейти от эпохи эмпирического конструирования к эпохе осознанного дизайна.

Оригинал статьи: https://arxiv.org/pdf/2601.10334.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-17 10:08