Искусственные временные ряды: новый взгляд через призму сетей

Автор: Денис Аветисян

В статье представлена инновационная методика генерации синтетических временных рядов, основанная на применении теории сложных сетей и квантильных графов.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал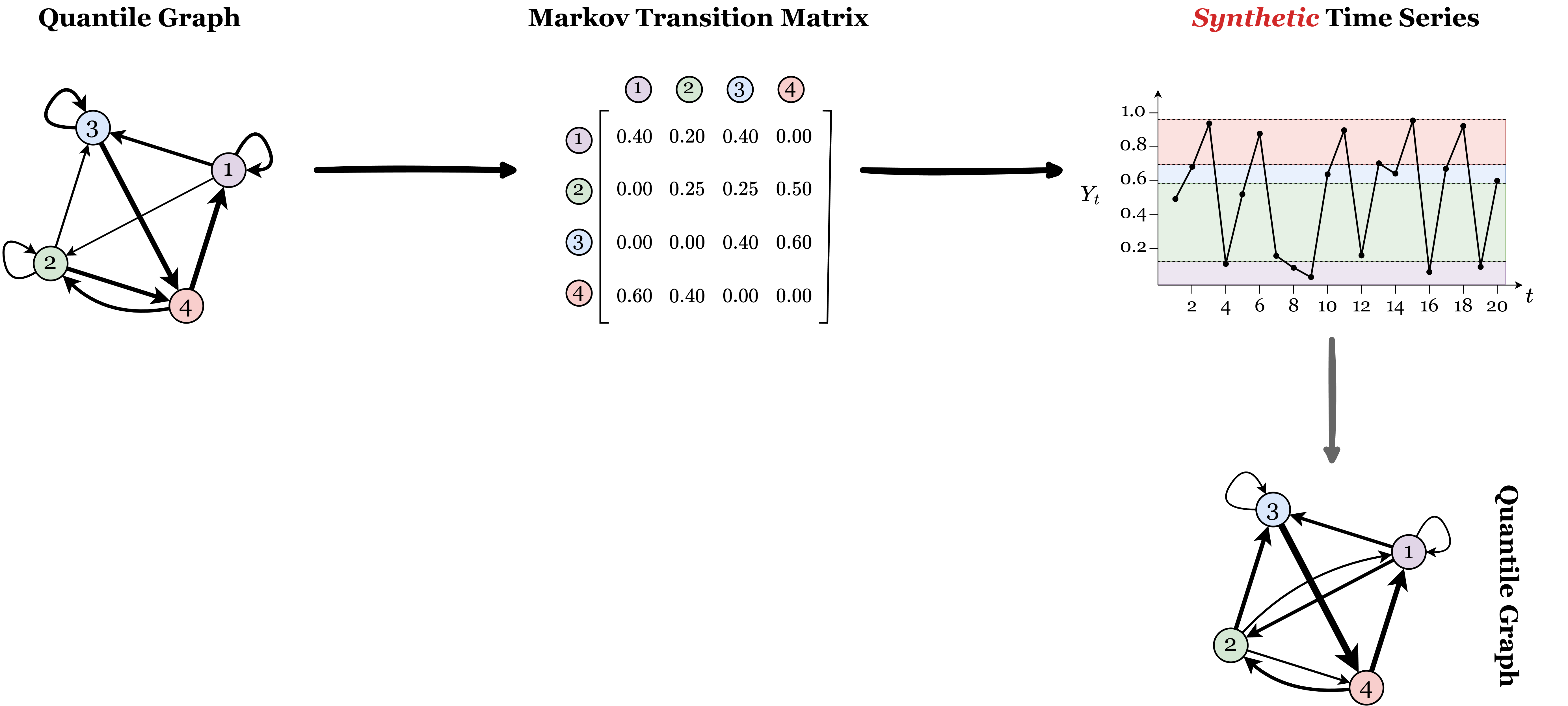

На основе метода сопоставления обратного квантильного графика (InvQG), применяемого к синтетическим временным рядам, устанавливается взаимосвязь между квантильными графиками и распределением вероятностей, что позволяет анализировать и прогнозировать динамику сложных систем.

Предложенный подход позволяет создавать реалистичные синтетические данные, сохраняя ключевые характеристики исходных временных рядов и являясь конкурентоспособной альтернативой методам глубокого обучения.

Несмотря на широкое применение временных рядов в машинном обучении и анализе данных, доступ к качественным наборам данных часто ограничен из-за проблем конфиденциальности и стоимости. В работе ‘Synthetic Time Series Generation via Complex Networks’ предложен новый подход к генерации синтетических временных рядов, основанный на отображении данных во входные графы квантилей. Показано, что данный метод позволяет создавать синтетические данные, сохраняющие статистические и структурные свойства исходных временных рядов, и обеспечивает конкурентоспособную альтернативу современным генеративным моделям на основе глубокого обучения. Возможно ли дальнейшее развитие данного подхода для создания еще более реалистичных и полезных синтетических данных для широкого спектра приложений?

Раскрывая Скрытые Закономерности: Вызовы Представления Временных Рядов

Традиционные методы анализа временных рядов часто оказываются неспособными уловить сложные взаимосвязи, присущие этим данным, что серьезно ограничивает точность аналитических выводов и прогнозов. В то время как простые статистические модели могут улавливать общие тенденции, они не учитывают нелинейные зависимости, сезонность, долгосрочные тренды и другие факторы, которые могут существенно влиять на динамику временного ряда. Это приводит к упрощенным представлениям реальности и, как следствие, к неточным прогнозам, особенно в условиях высокой волатильности или при наличии скрытых закономерностей. Неспособность адекватно отразить все нюансы временной зависимости данных затрудняет выявление критических точек, аномалий и потенциальных рисков, что делает традиционные подходы недостаточными для решения сложных задач анализа и прогнозирования в различных областях, от финансов и экономики до метеорологии и медицины.

Простое извлечение статистических характеристик, таких как автокорреляция, часто оказывается недостаточным для адекватного представления динамики временных рядов. Хотя автокорреляция может указать на наличие зависимости между точками во времени, она не способна зафиксировать сложные нелинейные взаимодействия, сезонность, тренды или долгосрочные зависимости, присущие многим реальным временным рядам. В результате, анализ, основанный исключительно на этих простых характеристиках, может привести к неточным прогнозам и упущению важных закономерностей. Например, временной ряд, демонстрирующий хаотическое поведение, может иметь низкую автокорреляцию, но при этом обладать сложной внутренней структурой, которую невозможно уловить с помощью традиционных статистических методов. Поэтому для полноценного анализа необходимо использовать подходы, способные учитывать более широкий спектр характеристик и структурных особенностей временных рядов.

Для эффективного анализа временных рядов недостаточно ограничиваться простыми статистическими сводками, такими как среднее значение или автокорреляция. Современные подходы подчеркивают необходимость выявления и использования структурной информации, скрытой внутри этих данных. Временные ряды обладают сложной внутренней организацией, отражающей динамику процессов, которые они представляют. Игнорирование этой структуры приводит к потере важной информации и снижает точность прогнозов. Разработка методов, способных извлекать и моделировать эти внутренние зависимости, например, с помощью анализа шаблонов, рекуррентных нейронных сетей или вейвлет-преобразований, позволяет получить более глубокое понимание данных и создавать более надежные модели для прогнозирования будущих значений. Таким образом, переход от простых статистических показателей к анализу структуры временных рядов является ключевым шагом в повышении эффективности анализа и прогнозирования.

Синтезированные временные ряды INAR успешно воспроизводят статистические характеристики оригинальных рядов, что подтверждается схожим видом их автокорреляционных функций и самих временных рядов.

Преобразование Времени в Топологию: Сетевое Представление

Квантильный граф представляет собой новый подход к отображению временного ряда в сеть, основанный на переходе значений через квантили. В основе метода лежит идея о том, что каждое значение временного ряда $x_i$ сопоставляется с узлом графа. Связь между двумя узлами $i$ и $j$ устанавливается, если $x_i$ и $x_j$ принадлежат к одному и тому же квантилю на разных временных шагах. Таким образом, переходы значений между квантилями фиксируют динамику временного ряда и отображаются в виде ребер графа. Этот метод позволяет преобразовать последовательность данных в топологическую структуру, пригодную для анализа с использованием инструментов теории графов.

Визуальный граф (Visibility Graph) позволяет уточнить сетевое представление временного ряда, акцентируя взаимосвязи между точками данных на основе принципа видимости. В рамках этой модели, два последовательных значения $x_i$ и $x_{i+1}$ считаются «видимыми» друг другу, если все промежуточные значения $x_j$ , где $i < j < i+1$ , находятся ниже прямой линии, соединяющей $x_i$ и $x_{i+1}$ . Наличие «видимости» формирует ребро в графе, что позволяет выделить нелинейные зависимости и корреляции, которые могут быть упущены при использовании стандартных методов анализа временных рядов. В результате, визуальный граф предоставляет более детализированное представление о структуре временного ряда, подчеркивая связи между точками, основанные на их взаимном расположении.

Представление временных рядов в виде графов позволяет применять алгоритмы анализа графов для выявления структурных особенностей данных. Извлечение топологических признаков, таких как степень узла, коэффициент кластеризации и центральность по посредничеству, предоставляет количественные характеристики сложности и взаимосвязей во временном ряду. Эти признаки могут быть использованы для классификации временных рядов, обнаружения аномалий и прогнозирования, обеспечивая альтернативный подход к традиционным методам анализа временных рядов, основанным на статистических и спектральных характеристиках. Например, изменения в топологических характеристиках графа, представляющего временной ряд, могут указывать на изменения в динамике данных, которые не видны при использовании стандартных методов.

Метод построения квантильного графика позволяет сопоставить распределение временного ряда с теоретическим распределением, как показано на примере, адаптированном из работ [Campanharo et al., 2011, Silva et al., 2021].

Воспроизведение Динамики: Генерация Синтетических Данных

Инверсный квантильный граф (Inverse Quantile Graph, IQG) позволяет осуществлять генерацию синтетических данных временных рядов на основе сетевых представлений. В основе метода лежит обратное преобразование отображения, которое изначально использовалось для построения сетевого представления из данных временного ряда. IQG определяет квантильные границы для каждого узла сети, а затем генерирует случайные значения в пределах этих границ, сохраняя статистические свойства исходных данных. Этот процесс позволяет создавать новые, реалистичные временные ряды, которые отражают динамику и зависимости, присутствующие в исходном наборе данных, без прямого копирования существующих образцов. Ключевым преимуществом является возможность контролировать характеристики генерируемых рядов через параметры, определяющие квантильные границы и вероятностное распределение генерируемых значений.

Для повышения качества и разнообразия синтетических временных рядов применяются продвинутые генеративные модели, такие как TimeGAN и DoppelGANger. TimeGAN использует генеративно-состязательную сеть (GAN) для обучения на распределении реальных данных и генерации новых последовательностей, имитирующих их статистические характеристики. DoppelGANger, в свою очередь, использует подход, основанный на обучении представлений временных рядов, что позволяет создавать более реалистичные и разнообразные синтетические данные, особенно в задачах, требующих сохранения долгосрочных зависимостей и сложных паттернов. Обе модели позволяют контролировать параметры генерации, обеспечивая возможность создания данных, соответствующих заданным требованиям и сценариям.

В процессе генерации синтетических данных временных рядов, матрица переходов Марковской цепи играет ключевую роль в моделировании вероятностных переходов между различными состояниями системы. Каждый элемент матрицы $P_{ij}$ представляет собой вероятность перехода из состояния $i$ в состояние $j$ . Использование такой матрицы позволяет создавать последовательности данных, отражающие статистические зависимости, наблюдаемые в реальных временных рядах. Это достигается путем последовательного применения матрицы переходов для определения вероятности каждого последующего состояния, основываясь на текущем состоянии, что обеспечивает реалистичность сгенерированных данных и позволяет моделировать динамику, характерную для исследуемого процесса.

Анализ методом t-SNE показывает, что InvQG, TimeGAN и DoppelGANger эффективно различают модели временных рядов, включая ARFIMA, ARIMA, GARCH, INAR, SETAR и HMM.

Оценка Качества: Полезность и Верность Синтетических Данных

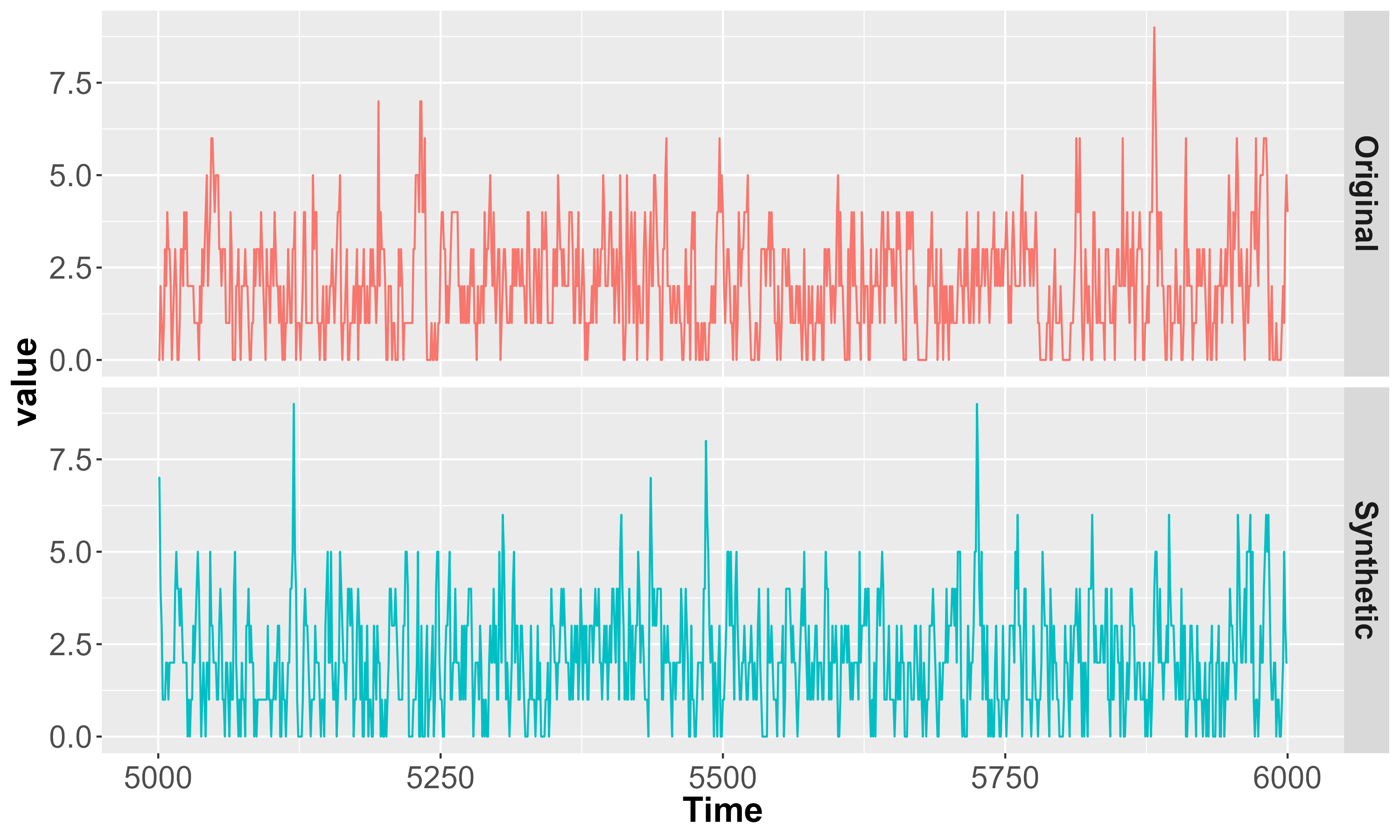
Качество синтетических временных рядов данных определяется двумя ключевыми аспектами: точностью — насколько достоверно они отражают характеристики исходных данных — и полезностью — их эффективностью в решении практических задач. Высокая точность обеспечивает соответствие статистических свойств, таких как среднее значение, дисперсия и корреляции, между оригинальными и синтетическими данными. Однако, даже при идеальном сохранении статистических свойств, данные могут оказаться бесполезными, если не способны поддерживать выполнение задач машинного обучения или анализа. Таким образом, оценка качества синтетических данных требует комплексного подхода, учитывающего оба параметра — как соответствие исходным данным, так и способность к эффективному использованию в целевых приложениях. Сочетание высокой точности и полезности является признаком успешной генерации синтетических данных, позволяющей расширить возможности анализа и моделирования без риска раскрытия конфиденциальной информации.

Оценка достоверности синтетических данных критически зависит от извлечения статистических признаков, позволяющего убедиться в сохранении ключевых характеристик исходных временных рядов. Этот процесс включает в себя вычисление и сравнение таких параметров, как среднее значение, дисперсия, автокорреляция и другие статистические показатели, между реальными и сгенерированными данными. Сохранение этих свойств необходимо для обеспечения того, чтобы синтетические данные адекватно отражали поведение оригинальных данных, что, в свою очередь, позволяет использовать их для обучения моделей машинного обучения и проведения анализа без внесения систематических искажений. Точное соответствие статистических признаков является фундаментальным критерием качества синтетических данных, гарантирующим их пригодность для практических применений и достоверность полученных результатов.

Извлечение топологических признаков играет ключевую роль в обеспечении практической ценности синтетических данных, позволяя проводить устойчивый анализ и моделирование. В отличие от традиционных методов, фокусирующихся на статистических характеристиках, топологический анализ исследует структуру и взаимосвязи в данных, выявляя закономерности, которые могут быть упущены при обычном рассмотрении. Это особенно важно для временных рядов, где сложные зависимости и нелинейные взаимосвязи часто определяют поведение системы. Применение топологических методов позволяет оценить, насколько хорошо синтетические данные сохраняют эти структурные особенности, обеспечивая надежность результатов при использовании в последующих задачах, таких как прогнозирование, обнаружение аномалий и классификация. В результате, синтетические данные, прошедшие оценку с помощью топологического анализа, демонстрируют повышенную устойчивость к шуму и искажениям, что делает их более полезными для широкого спектра прикладных задач.

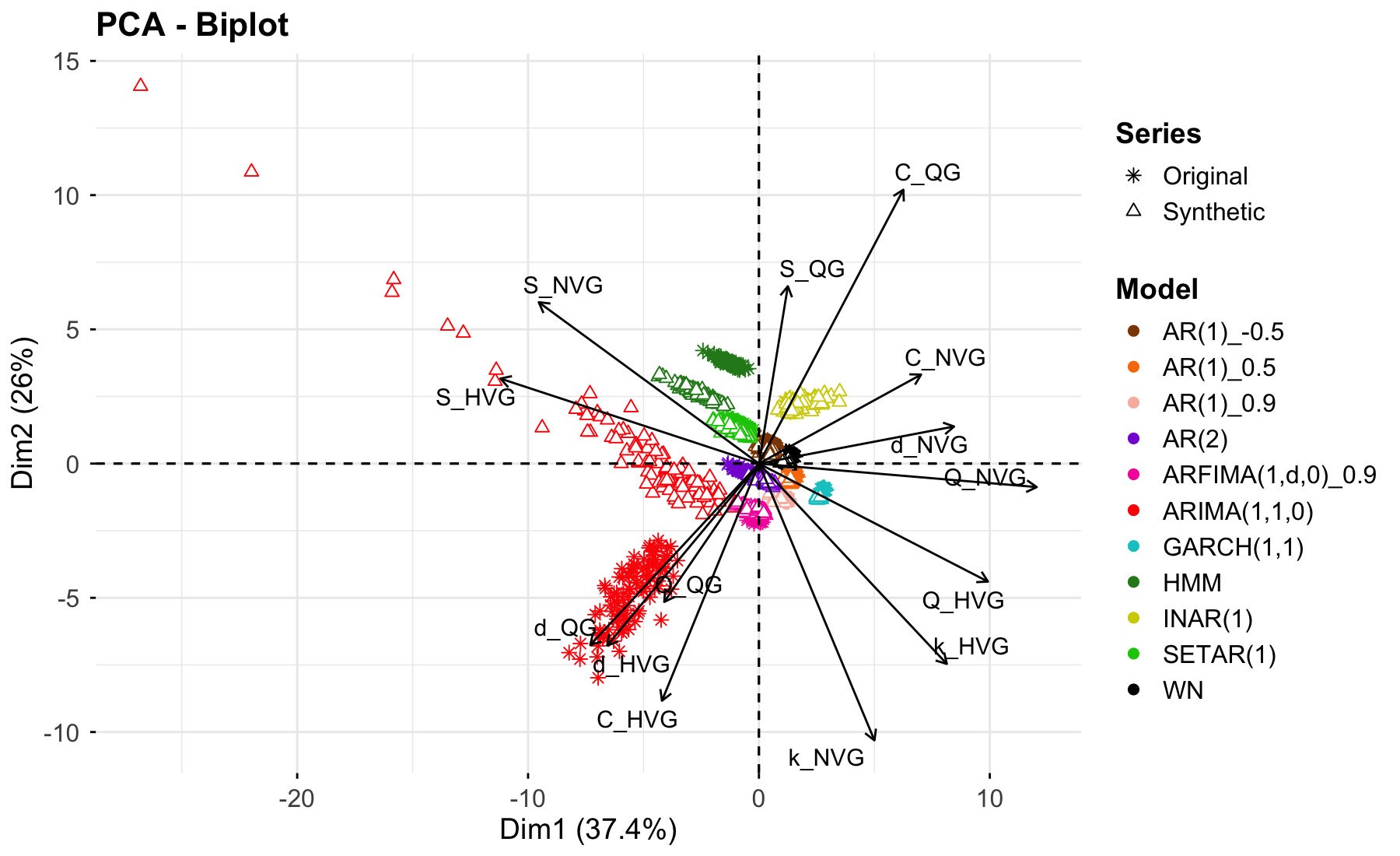
Визуализации, полученные с помощью метода главных компонент (PCA), демонстрируют тесное сближение кластеров оригинальных и синтетических данных в различных моделях временных рядов. Это указывает на эффективное сохранение статистических характеристик, сравнимое с результатами, достигнутыми с использованием генеративно-состязательных сетей (GAN). Такое сближение подтверждает, что синтетические данные успешно воспроизводят ключевые закономерности и зависимости, присутствующие в исходных данных, что делает их пригодными для использования в последующих аналитических задачах и моделях.

Визуализация с использованием алгоритма t-SNE подтверждает, что метод, основанный на квантовых генеративных моделях (QG), демонстрирует более высокую степень соответствия между распределениями синтетических и исходных данных по сравнению с такими подходами, как TimeGAN и DoppelGANger. Данный анализ позволил выявить, что QG-метод последовательно генерирует синтетические данные, чья структура и статистические свойства более точно отражают характеристики оригинальных временных рядов. В частности, кластеры, сформированные на основе синтетических данных, полученных с помощью QG, более тесно прилегают к кластерам, представляющим исходные данные, что свидетельствует о более эффективном моделировании сложных зависимостей и сохранении ключевой информации во временных рядах. Результаты указывают на потенциальное преимущество QG-метода в задачах, требующих высокой точности воспроизведения статистических характеристик данных, например, в анализе трендов и прогнозировании.

Анализ главных компонент (PCA) продемонстрировал способность разработанного метода успешно захватывать ключевые характеристики временных рядов, подтверждая, что синтетические данные сохраняют важные статистические свойства оригинальных данных. Визуализация результатов PCA показала близкое скопление оригинальных и синтетических данных для различных моделей временных рядов, что свидетельствует о высокой степени сохранения статистических признаков, сопоставимой с результатами, полученными с использованием генеративно-состязательных сетей (GAN). Однако, несмотря на достигнутый прогресс, полное воспроизведение всех тонкостей и сложности реальных временных рядов остается сложной задачей. Некоторые нюансы, связанные с нелинейными зависимостями и долгосрочными трендами, требуют дальнейшей оптимизации алгоритмов генерации синтетических данных для достижения максимальной точности и реалистичности.

Анализ главных компонент (ГК) показывает, что синтетические временные ряды, представленные треугольниками, эффективно воспроизводят структуру исходных данных (обозначенных звёздочками), при этом вклад различных топологических признаков (NetF), определяемый длиной стрелок, в формирование ГК является сопоставимым.

Исследование демонстрирует, что попытки искусственного создания временных рядов неизбежно приводят к построению сложных взаимосвязей, напоминающих сети. Этот подход, основанный на графах квантилей, подчеркивает, что даже в кажущихся случайных данных проявляется закономерность и зависимость. Кен Томпсон однажды заметил: «Всё стремится к зависимости». Эта фраза находит глубокий отклик в данной работе, поскольку она показывает, как даже при генерации синтетических данных, невозможно избежать формирования связей между точками данных. Авторы предлагают не просто создание данных, но и моделирование их внутренней структуры, признавая, что любые системы, даже искусственные, подвержены закономерностям и взаимосвязям, которые рано или поздно проявятся в их поведении.

Что же дальше?

Представленный подход, переводящий временные ряды в сложные сети, обнажает скрытую истину: данные — это не поток значений, а паутина взаимосвязей. Однако, в каждом кроне этого графа скрыт страх перед хаосом. Попытка сохранить характеристики временного ряда через структуру сети — это, по сути, лишь отсрочка энтропии, а не её победа. Неизбежно возникнет вопрос о масштабируемости — как эта модель поведет себя с рядами, где количество узлов сети экспоненциально растет? Этот паттерн выродится через три релиза, если не будет учтена динамика изменения связей между узлами.

Надежда на идеальную архитектуру для генерации синтетических данных — это форма отрицания энтропии. Следующим шагом видится не столько усложнение модели, сколько поиск способов внедрения в неё элементов самоорганизации, позволяющих сети адаптироваться к изменяющимся характеристикам исходных данных. Необходимо сместить фокус с точного копирования статистических свойств на эмуляцию процессов, порождающих эти ряды — то есть, перейти от описания к моделированию причинности.

В конечном счете, истинная ценность этого подхода — не в создании идеальных синтетических данных, а в предоставлении нового взгляда на природу временных рядов. Это — не инструмент, а экосистема, и её развитие подчиняется законам эволюции, а не предписаниям архитектора.

Оригинал статьи: https://arxiv.org/pdf/2601.22879.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-03 01:03