Автор: Денис Аветисян
Новая методика позволяет создавать синтетические данные для выявления систематических искажений в моделях прогнозирования временных рядов.
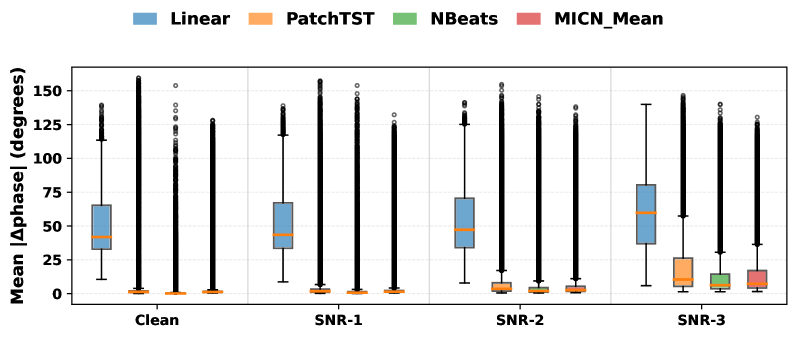
В статье представлен TimeSynth — фреймворк для генерации синтетических данных, демонстрирующий склонность линейных моделей к тривиальным колебаниям и устойчивость нелинейных моделей к изменениям в данных.
Несмотря на широкое применение, вопрос о превосходстве сложных нелинейных моделей над простыми линейными в прогнозировании временных рядов остается дискуссионным. В данной работе, представленной под названием ‘TimeSynth: A Framework for Uncovering Systematic Biases in Time Series Forecasting’, предложен структурированный подход к генерации синтетических данных, эмулирующих ключевые свойства реальных временных рядов, включая нестационарность, периодичность и фазовую модуляцию. Полученные результаты демонстрируют, что линейные модели склонны к тривиальной осцилляции вне зависимости от сложности сигнала, в то время как нелинейные модели демонстрируют лучшую адаптивность и устойчивость. Каким образом предложенный фреймворк позволит более точно определить условия, при которых различные подходы к прогнозированию оказываются наиболее эффективными?
Разоблачение границ: синтетические сигналы и ограничения базовых моделей
Точное прогнозирование временных рядов имеет решающее значение в широком спектре дисциплин — от финансов и метеорологии до нейробиологии и инженерии. Однако, несмотря на значительный прогресс в области машинного обучения, многие существующие модели демонстрируют ограниченные возможности при работе со сложными, нелинейными временными зависимостями. Сложность заключается в том, что реальные данные редко соответствуют простым математическим функциям; они часто содержат скрытые тренды, сезонность, выбросы и другие факторы, которые трудно уловить с помощью традиционных методов. Это приводит к неточностям в прогнозах, которые могут иметь серьезные последствия в критических областях, требующих высокой степени надежности и предсказуемости. Неспособность моделей адекватно отражать реальную динамику временных рядов подчеркивает необходимость разработки более совершенных алгоритмов и подходов к моделированию.
Традиционные методы прогнозирования временных рядов, такие как линейные модели и ARIMA, несмотря на свою вычислительную эффективность, часто демонстрируют неожиданную неспособность улавливать тонкие и сложные временные зависимости. Исследования показывают, что при анализе нелинейных сигналов эти модели склонны к упрощению, игнорируя важные нюансы и переоценивая влияние простых колебаний. Это приводит к существенным погрешностям в прогнозах, особенно при работе с данными, содержащими сложные паттерны и нелинейные тренды. Неспособность адекватно отразить истинную динамику сигнала ограничивает их применение в задачах, требующих высокой точности и детализации прогнозов, подчеркивая необходимость разработки более продвинутых алгоритмов для анализа сложных временных рядов.
Исследования показали, что базовые модели временных рядов, такие как линейные модели и ARIMA, демонстрируют систематическую предвзятость, известную как «линейная предвзятость». Несмотря на сложность исходных сигналов, эти модели склонны упрощать данные, сводя их к простым колебаниям. Данное явление подтверждается значительными ошибками в оценке частоты и амплитуды — Frequency Error и Amplitude Error соответственно — которые наблюдались в ходе оценок. Фактически, модели «схлопываются» до базовых осцилляций, игнорируя более тонкие и сложные паттерны, присутствующие в данных, что существенно ограничивает их способность к точным прогнозам.

Контролируемая сложность: сила генерации синтетических данных
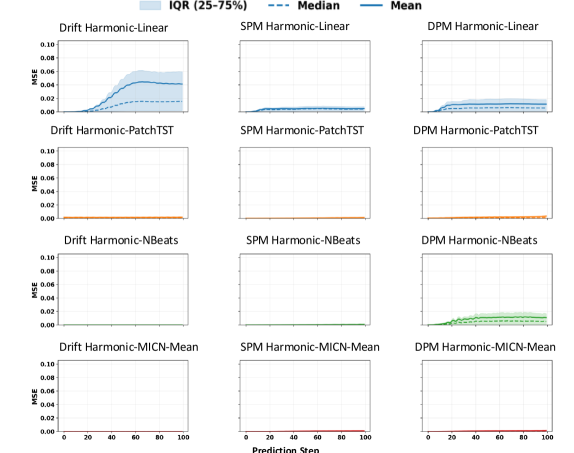
Для генерации разнообразных синтетических временных рядов используется библиотека `TimeSynth`. Она позволяет создавать сигналы различной сложности — от простых гармонических колебаний до комбинаций, включающих дрифт, SPM-гармонические и DPM-гармонические компоненты. Это обеспечивает возможность точного контроля над параметрами сигнала, такими как частота, амплитуда и фаза, и позволяет создавать данные с заданными характеристиками для тестирования и валидации алгоритмов анализа временных рядов.
Генерация сигналов, таких как сигналы с дрейфом гармоники (Drift Harmonic Signals), сигналы с переменной частотой гармоники (SPM-Harmonic Signals) и сигналы с динамической фазовой модуляцией гармоники (DPM-Harmonic Signals), обеспечивает точный контроль над ключевыми параметрами временных рядов. В частности, пользователи могут независимо задавать частоту f, амплитуду A и фазу φ каждой гармоники, что позволяет создавать синтетические данные с заранее известными характеристиками. Такой уровень контроля необходим для детального анализа и тестирования алгоритмов обработки временных рядов, а также для оценки их чувствительности к отдельным параметрам сигнала.
Использование генерации синтетических данных позволяет проводить систематическую оценку производительности моделей в контролируемых условиях. Такой подход позволяет отделить внутренние ограничения самой модели от проблем, связанных со спецификой реальных данных. Это достигается путем создания наборов данных с заранее известными характеристиками, что позволяет точно определить, какие аспекты данных вызывают затруднения у модели, и какие ограничения присущи алгоритму. В результате, можно более эффективно оптимизировать модели и улучшить их обобщающую способность, а также более точно интерпретировать результаты анализа данных.

Преодолевая границы: современные архитектуры для прогнозирования временных рядов
Современные методы глубокого обучения, такие как `Transformers` (используемые в `Autoformer` и `PatchTST`), `Convolutional Neural Networks` (применяемые в `ModernTCN` и `MICN`) и частотно-доменные модели, например `FreTS`, предлагают потенциальные улучшения по сравнению с традиционными подходами к прогнозированию временных рядов. `Transformers` используют механизм самовнимания для моделирования долгосрочных зависимостей, в то время как `CNN` применяют сверточные фильтры для извлечения локальных признаков и паттернов. Модели частотного домена, такие как `FreTS`, анализируют временные ряды в частотной области, что позволяет эффективно улавливать периодические компоненты и тренды. Эти архитектуры способны более эффективно моделировать сложные временные зависимости, чем линейные модели и традиционные статистические методы.
Современные архитектуры прогнозирования временных рядов используют разнообразные механизмы для захвата временных зависимостей. Модели на основе `Transformers`, такие как `Autoformer` и `PatchTST`, применяют механизм самовнимания (self-attention) для взвешивания различных точек временного ряда, выявляя значимые корреляции. Сверточные нейронные сети (CNN), используемые в `ModernTCN` и `MICN`, применяют сверточные фильтры для извлечения локальных шаблонов и признаков во временных данных. Альтернативно, частотные модели, например `FreTS`, анализируют временной ряд в частотной области, выявляя доминирующие частоты и периодичности. Каждая из этих методик позволяет моделировать временные зависимости различными способами, что позволяет адаптироваться к различным характеристикам данных и повысить точность прогнозирования.
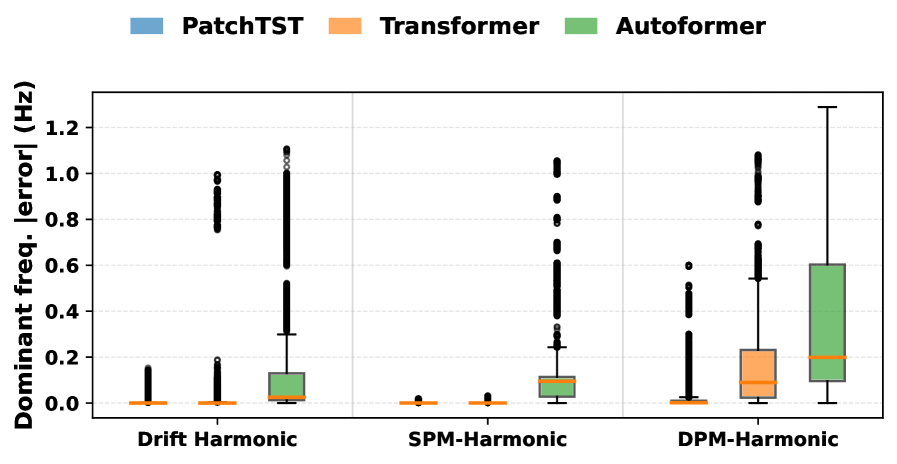
Целью оценки представленных моделей — `Transformers` (например, `Autoformer` и `PatchTST`), `Convolutional Neural Networks` (`ModernTCN` и `MICN`) и моделей частотной области (`FreTS`) — на синтетическом наборе данных является выявление наиболее эффективных архитектур для моделирования сложных динамик временных рядов. В ходе экспериментов была продемонстрирована способность данных моделей превосходить линейные модели, что подтверждается значительно сниженной ошибкой амплитуды (MAE) и улучшенной ошибкой фазы. Низкие значения MAE указывают на более точное прогнозирование величины значений временного ряда, а улучшенная точность фазы свидетельствует о более верном определении моментов времени, соответствующих пикам и провалам в данных.
Стресс-тесты и устойчивость: оценка производительности модели при смещении распределения
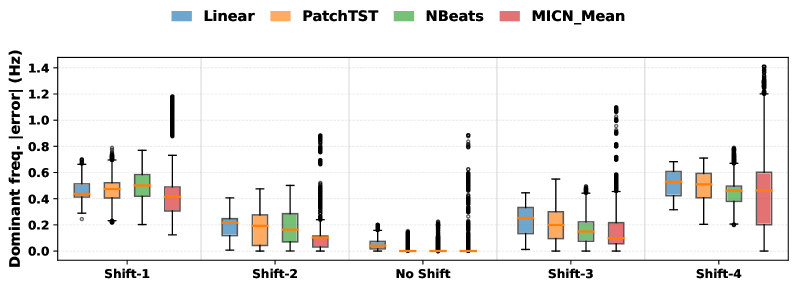
Для оценки способности обученных моделей к обобщению и поддержанию точности в условиях реальных данных, они подвергались намеренным изменениям в распределении входных данных и добавлению шумовых возмущений. Этот процесс, известный как “стресс-тестирование”, позволяет выявить устойчивость моделей к отклонениям от идеальных условий обучения. В ходе исследования изменялись характеристики входных данных, чтобы имитировать сценарии, которые могут возникнуть в процессе эксплуатации, а также вносились случайные помехи для оценки влияния неполноты или искажения информации. Такой подход позволяет определить, насколько надежно модель сможет предсказывать результаты, даже когда входящие данные отличаются от тех, на которых она обучалась, и является критически важным этапом перед внедрением модели в практическое использование.
Для количественной оценки точности прогнозирования использовался комплекс метрик, включающий ошибку по частоте, ошибку по амплитуде и фазовую ошибку. Результаты анализа показали, что нелинейные модели демонстрируют значительно более низкие значения этих ошибок по сравнению с линейными аналогами. В частности, снижение ошибок по всем трем метрикам указывает на более высокую способность нелинейных моделей улавливать сложные зависимости в данных и адаптироваться к их изменениям. Такое превосходство особенно заметно при прогнозировании нелинейных временных рядов, где традиционные линейные методы часто оказываются неэффективными. Полученные данные подтверждают, что использование нелинейных моделей может существенно повысить надежность и точность прогнозов в различных областях применения.
Оценка чувствительности модели к изменениям входных данных и наличию шумов имеет решающее значение для успешного внедрения в реальные условия, где данные редко бывают идеальными, а условия эксплуатации могут существенно отличаться от обучающей выборки. Проведенный статистический анализ с уровнем значимости p < 0.001 подтверждает, что устойчивость модели к таким возмущениям напрямую влияет на ее способность к обобщению и надежности прогнозов. Это означает, что модели, демонстрирующие меньшую чувствительность к отклонениям в данных, способны сохранять высокую точность даже в неблагоприятных условиях, что критически важно для практического применения и принятия обоснованных решений на основе их предсказаний.
К фундаментальным моделям для временных рядов: взгляд в будущее
Результаты синтетической оценки, проведенной в рамках данного исследования, служат основой для разработки так называемых фундаментальных моделей прогнозирования временных рядов. Эти модели, в отличие от традиционных подходов, стремятся к объединению методов обучения представлений и непосредственно прогнозирования, что позволяет им эффективно адаптироваться к различным областям применения и демонстрировать улучшенную обобщающую способность. Используя синтетические данные для предварительного обучения, исследователи добиваются создания моделей, способных к более точным и надежным прогнозам в сложных реальных сценариях, учитывая при этом баланс между стабильностью и точностью предсказаний. Такой подход открывает новые возможности для автоматизации анализа данных и принятия решений, основанных на прогнозах временных рядов в различных областях, от финансов и энергетики до здравоохранения и логистики.
Разрабатываемые модели стремятся к объединению обучения представлений и прогнозирования временных рядов в различных областях, что открывает возможности для переноса знаний и повышения обобщающей способности. Вместо разработки отдельных моделей для каждой задачи, предлагается создание универсальной архитектуры, способной извлекать общие закономерности из разнообразных данных временных рядов. Это позволяет модели, обученной на большом объеме синтетических или реальных данных из одной области, эффективно адаптироваться к новым задачам в других областях, требуя значительно меньше данных для переобучения и демонстрируя повышенную устойчивость к шуму и выбросам. Такой подход позволяет преодолеть ограничения традиционных методов, обеспечивая более точные и надежные прогнозы в сложных и динамичных условиях.
Сочетание различных архитектурных подходов и использование синтетических данных для предварительного обучения открывает новые перспективы в области точного и надежного прогнозирования временных рядов в сложных реальных сценариях. Данный подход позволяет преодолеть фундаментальный компромисс между стабильностью и точностью модели. Предварительное обучение на искусственно сгенерированных данных, охватывающих широкий спектр паттернов и аномалий, позволяет моделям усваивать общие принципы, применимые к различным временным рядам. Интеграция сильных сторон различных архитектур, таких как рекуррентные нейронные сети, трансформеры и свёрточные сети, позволяет создавать гибридные модели, способные эффективно обрабатывать как локальные, так и глобальные зависимости во временных данных. Это, в свою очередь, способствует повышению обобщающей способности и надежности прогнозов, особенно в условиях ограниченного количества исторических данных или при наличии шумов и выбросов.
Исследование, представленное в данной работе, демонстрирует, как линейные модели склонны к упрощению сложных динамик временных рядов, сводя их к тривиальным колебаниям. Это напоминает естественный процесс старения систем — стремление к состоянию минимальной энергии. Однако, в отличие от линейных моделей, нелинейные системы проявляют адаптивность и устойчивость к изменениям, подобно организмам, которые учатся дышать вместе с энтропией. Как однажды заметил Линус Торвальдс: «Плохой код похож на раковую опухоль: он растет, пока не убьет систему». Аналогично, упрощенные модели, не способные учесть сложность данных, могут привести к искаженным прогнозам и, в конечном итоге, к сбою системы. Важно помнить, что системы учатся стареть достойно, и наблюдение за этим процессом может быть столь же ценно, как и попытки его ускорить.
Куда Ведет Время?
Представленная работа, выявляя систематические искажения в прогнозировании временных рядов, лишь подтверждает старую истину: любое улучшение стареет быстрее, чем ожидалось. Линейные модели, неизбежно схлопывающиеся до тривиальных колебаний, демонстрируют не столько их несостоятельность, сколько неизбежность энтропии в любой системе. Более устойчивые нелинейные модели, безусловно, заслуживают дальнейшего изучения, однако и они не избавлены от необходимости адаптироваться к постоянно меняющейся среде.
Особый интерес представляет вопрос о природе самих искажений. Анализ в частотной области, безусловно, является важным шагом, но он не исчерпывает всех возможностей. Следующим этапом видится разработка метрик, способных более точно отражать динамику систем, подверженных сдвигу распределений. Ведь откат — это не просто возвращение к исходной точке, а путешествие назад по стрелке времени, в котором информация о прошлом искажается и упрощается.
В конечном итоге, задача заключается не в создании идеального прогноза, а в понимании того, как системы стареют. Необходимо признать, что любая модель — это лишь приближение, а время — не метрика, а среда, в которой эти приближения неизбежно деградируют. Иными словами, важно не столько предсказать будущее, сколько достойно встретить неизбежное.
Оригинал статьи: https://arxiv.org/pdf/2602.11413.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- SOL ПРОГНОЗ. SOL криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- HYPE ПРОГНОЗ. HYPE криптовалюта
- SUI ПРОГНОЗ. SUI криптовалюта
- FARTCOIN ПРОГНОЗ. FARTCOIN криптовалюта
2026-02-14 03:10