Интеллектуальное управление портфелем: обучение с подкреплением на службе инвестора

Автор: Денис Аветисян

Новый подход к оптимизации инвестиционного портфеля использует алгоритмы обучения с подкреплением для достижения финансовых целей в условиях меняющегося рынка.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал

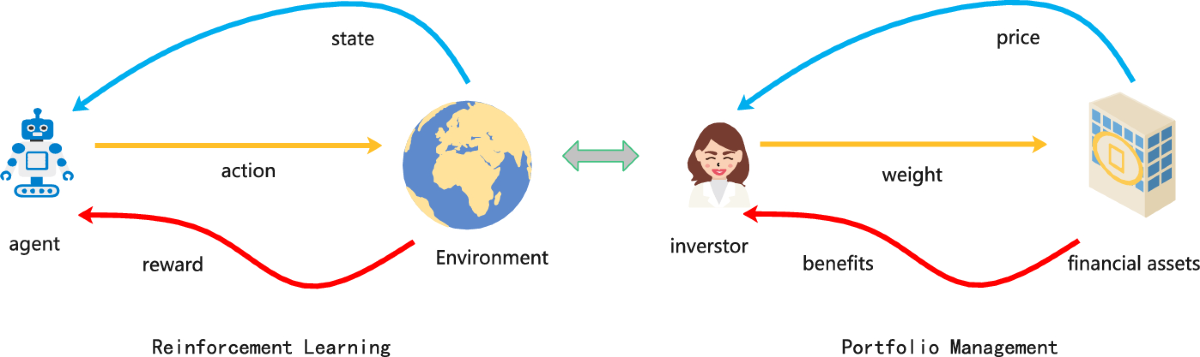
Оптимизация портфеля активов рассматривается через призму обучения с подкреплением, позволяя выявить стратегии, максимизирующие доходность за счет баланса между исследованием новых возможностей и использованием проверенных, что отражает динамику между надеждами и страхами инвестора.

В статье рассматривается применение G-Learning и алгоритма GIRL для максимизации коэффициента Шарпа и минимизации взносов при оптимизации портфеля в заданные временные рамки.

Несмотря на растущую популярность алгоритмических стратегий, оптимизация инвестиционного портфеля с учетом как целевой доходности, так и минимизации периодических взносов остается сложной задачей. В работе «Reinforcement Learning for Portfolio Optimization with a Financial Goal and Defined Time Horizons» предложен подход, основанный на алгоритме G-Learning, дополненном параметрической оптимизацией GIRL, демонстрирующий улучшение коэффициента Шарпа до 0.483 в условиях высокой волатильности рынка. Полученные результаты свидетельствуют о том, что методы обучения с подкреплением способны эффективно адаптировать портфельные стратегии к потребностям инвестора. Возможно ли дальнейшее повышение эффективности подобных алгоритмов за счет интеграции с более сложными моделями прогнозирования рыночной динамики?

Пределы Традиционной Оптимизации Портфеля: За пределами диверсификации

Классические методы оптимизации портфеля, такие как современная портфельная теория, опираются на анализ прошлых данных и предположения о будущем поведении активов, что может приводить к упущению возможностей, возникающих в динамично меняющихся рыночных условиях. Данный подход предполагает, что исторические закономерности сохранятся в будущем, что не всегда соответствует действительности, особенно в периоды высокой волатильности или структурных изменений в экономике. Например, корреляции между активами, определенные на основе прошлых данных, могут значительно измениться, делая оптимизированный портфель менее эффективным, чем предполагалось. В результате, инвесторы, полагающиеся исключительно на исторические данные, рискуют недооценить потенциальные риски и упустить возможности для повышения доходности, особенно в условиях быстро меняющегося инвестиционного ландшафта. Необходимость адаптации к текущим условиям и прогнозирования будущих трендов становится ключевым фактором для успешной оптимизации портфеля в долгосрочной перспективе.

Коэффициент Шарпа, являясь ценным инструментом оценки доходности с учетом риска, имеет существенные ограничения. Он предполагает, что инвесторы принимают решения исключительно на основе математического ожидания и дисперсии, игнорируя индивидуальные финансовые цели и горизонты планирования. В реальности, предпочтения инвесторов могут быть разнообразными — от сохранения капитала до агрессивного роста — и зависеть от личных обстоятельств. Более того, коэффициент Шарпа статичен и не учитывает динамику рынка, изменения в волатильности активов или возникающие возможности для перебалансировки портфеля. Таким образом, полагаться исключительно на коэффициент Шарпа при построении инвестиционной стратегии может привести к неоптимальным результатам, не соответствующим конкретным потребностям и целям инвестора.

Традиционные методы управления инвестиционным портфелем зачастую испытывают трудности при учете регулярных взносов и адаптации стратегии к конкретным финансовым целям, например, накоплению средств для будущей крупной покупки. Классические модели оптимизации, фокусируясь на текущем состоянии активов и исторической волатильности, не всегда эффективно моделируют влияние постоянного притока капитала и изменяющихся потребностей инвестора. В результате, портфель может оказаться недостаточно оптимизированным для достижения поставленной цели в заданный срок, поскольку не учитываются динамические факторы, такие как время до предполагаемой траты и требуемый уровень гарантии достижения цели. Поэтому, при планировании долгосрочных инвестиций, особенно с регулярными пополнениями, необходимо учитывать не только текущую доходность и риск, но и индивидуальные финансовые горизонты и конкретные цели инвестора.

Модель G-обучения с фиксированными параметрами обеспечивает стабильную доходность портфеля во времени.

Обучение с Подкреплением: Новый Подход к Оптимизации Портфеля

Обучение с подкреплением предоставляет эффективный подход к оптимизации портфеля, позволяя агенту разрабатывать оптимальные торговые стратегии посредством взаимодействия с симулированной рыночной средой. В отличие от традиционных методов, требующих заранее определенных моделей рынка, обучение с подкреплением позволяет агенту адаптироваться к изменяющимся рыночным условиям и выявлять сложные зависимости между активами. Агент, действуя в симуляции, получает вознаграждение за прибыльные сделки и штрафы за убыточные, что позволяет ему постепенно улучшать свою торговую политику посредством проб и ошибок. Этот итеративный процесс позволяет агенту находить стратегии, максимизирующие долгосрочную доходность при заданном уровне риска, без необходимости явного программирования правил торговли.

В отличие от Q-обучения, которое стремится к определению оптимальной политики в детерминированной среде, G-обучение использует вероятностные подходы для учета неопределенности рыночных условий. Это достигается за счет моделирования переходов состояний как вероятностных, а не детерминированных, что позволяет агенту оценивать риски и адаптировать свою стратегию к различным сценариям. В G-обучении, вместо оценки $Q(s,a)$, оценивается функция ценности $V(s)$, что позволяет агенту выбирать действия на основе вероятности получения максимальной ожидаемой награды, а не только на основе текущей оценки действия. Это особенно важно в финансовых рынках, где будущие цены активов подвержены значительной неопределенности.

Алгоритм G-Learning использует функцию вознаграждения (Reward Function) для количественной оценки привлекательности различных состояний портфеля. Эта функция назначает числовое значение каждому состоянию, отражающее его желательность с точки зрения максимизации долгосрочной прибыли и управления рисками. Формирование функции вознаграждения критически важно: она должна учитывать не только текущую доходность, но и факторы, связанные с волатильностью активов и потенциальными убытками. Таким образом, агент стремится максимизировать кумулятивное вознаграждение, получаемое в процессе взаимодействия с рыночной средой, что позволяет ему разрабатывать оптимальные стратегии управления портфелем, учитывающие как доходность, так и риск. Оценка функции вознаграждения может включать такие метрики, как коэффициент Шарпа или другие показатели эффективности инвестиций, адаптированные к конкретным задачам оптимизации.

Модель G-learner позволяет корректировать доходность портфеля с течением времени.

Вывод Намерений Инвестора: Роль Обратного Обучения с Подкреплением

Обратное обучение с подкреплением (IRL) представляет собой метод вывода скрытой функции вознаграждения на основе наблюдаемого поведения инвесторов, такого как паттерны торговли или корректировки портфеля. В отличие от традиционного обучения с подкреплением, где функция вознаграждения задается заранее, IRL стремится реконструировать эту функцию, анализируя последовательность действий инвестора. Данный подход позволяет идентифицировать цели и предпочтения, которые мотивируют действия инвестора, используя наблюдаемые данные о его торговой активности и изменениях в структуре портфеля. Результирующая функция вознаграждения представляет собой математическую модель, отражающую приоритеты инвестора, например, максимизацию прибыли, минимизацию риска или достижение конкретных финансовых целей. Анализируя последовательность действий и соответствующую функцию вознаграждения, можно получить представление о стратегии, которую инвестор стремится реализовать.

Алгоритм GIRL использует обратное обучение с подкреплением (IRL) для определения параметров функции вознаграждения внутри G-обучения. Этот процесс позволяет системе адаптироваться к индивидуальным предпочтениям инвесторов, анализируя их поведение и выявляя скрытые цели. IRL позволяет оценить, какие факторы инвестор считает наиболее важными при принятии решений, такие как доходность, риск или горизонт инвестирования. Оптимизируя функцию вознаграждения на основе этих параметров, G-обучение формирует инвестиционные стратегии, соответствующие конкретным предпочтениям каждого инвестора, что значительно повышает эффективность портфельного управления по сравнению с универсальными подходами.

Комбинирование алгоритмов обратного обучения с подкреплением (IRL) и G-обучения позволяет перейти от универсальных стратегий оптимизации портфеля к персонализированным решениям, соответствующим конкретным финансовым целям инвестора. Традиционные методы часто используют предопределенные функции вознаграждения, которые могут не отражать индивидуальные предпочтения и рисковые профили. IRL, анализируя наблюдаемое поведение инвестора, такое как паттерны торговли и корректировки портфеля, позволяет вывести функцию вознаграждения, которая наилучшим образом объясняет его действия. Эта функция затем используется в G-обучении для оптимизации портфеля, что обеспечивает более точное соответствие стратегии инвестирования индивидуальным целям и предпочтениям инвестора, повышая потенциальную доходность и снижая риски.

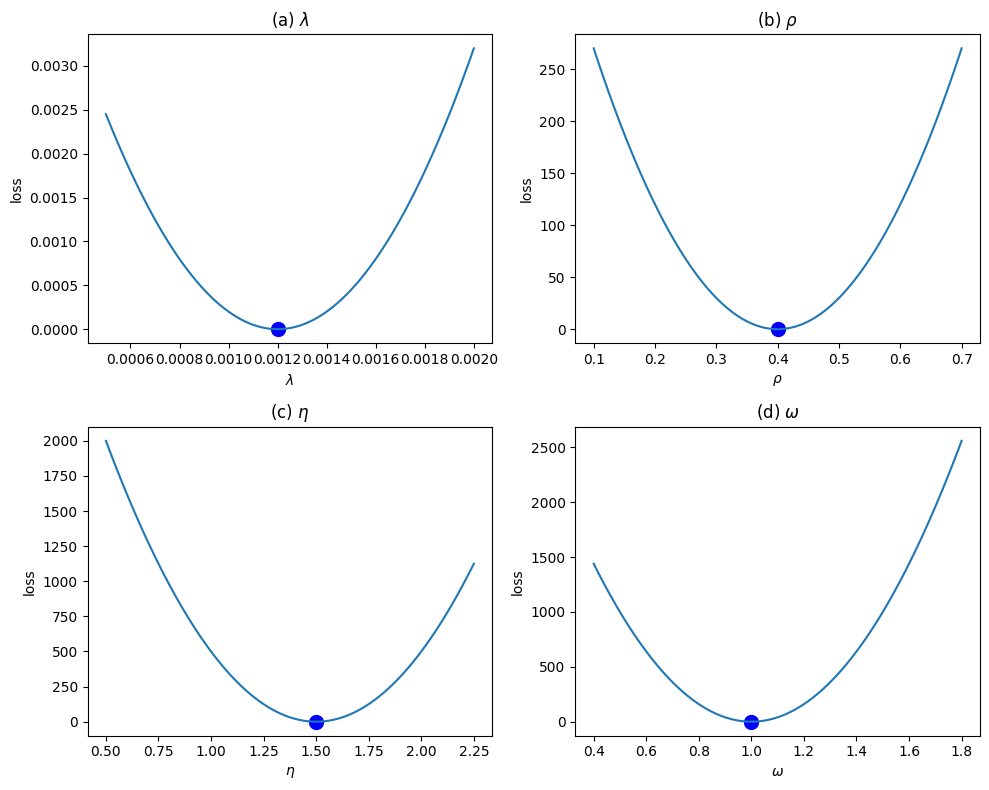
Обучение параметров с использованием модели GIRL демонстрирует стабильную сходимость к оптимальным значениям.

Учет Динамики Рынка: Моделирование Неопределенности и Максимизация Доходности

Несмотря на то, что волатильность рынка способна негативно влиять на доходность портфеля, современные алгоритмы, такие как G-Learning, демонстрируют способность адаптироваться к изменяющимся условиям и эффективно снижать риски. В отличие от традиционных стратегий, которые часто оказываются неэффективными в периоды турбулентности, G-Learning использует принципы обучения с подкреплением для динамической корректировки инвестиционной стратегии. Алгоритм анализирует текущую рыночную ситуацию и, основываясь на исторических данных и прогнозах, оптимизирует состав портфеля, стремясь к максимальной доходности при заданном уровне риска. Такой подход позволяет не только минимизировать потери в периоды спада, но и извлекать выгоду из краткосрочных колебаний цен, обеспечивая более стабильный и предсказуемый результат инвестиций, даже в условиях высокой волатильности.

Для создания правдоподобной среды обучения и оценки агентов, использующих обучение с подкреплением, применяется моделирование динамики цен активов с использованием геометрического броуновского движения. Этот математический инструмент, описывающий случайные изменения цен, позволяет генерировать реалистичные сценарии рыночных колебаний. В рамках исследования, $S_t = S_0e^{(\mu — \frac{\sigma^2}{2})t + \sigma W_t}$ — уравнение, лежащее в основе симуляций, где $S_t$ — цена актива в момент времени $t$, $S_0$ — начальная цена, $\mu$ — средняя доходность, $\sigma$ — волатильность, а $W_t$ — винеровский процесс. Такой подход позволяет агентам обучения с подкреплением адаптироваться к различным рыночным условиям и разрабатывать эффективные стратегии управления портфелем в условиях неопределенности, прежде чем применять их к реальным данным.

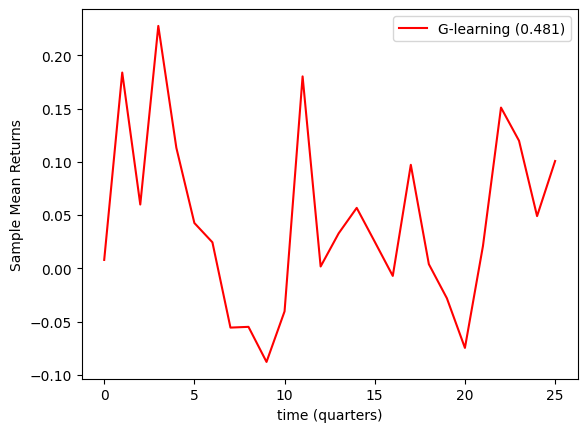
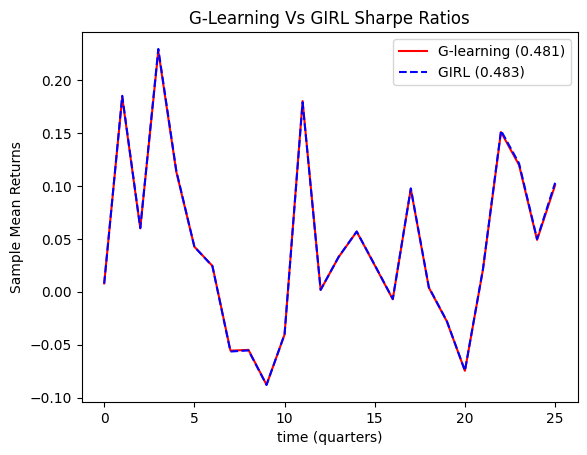
Исследование демонстрирует, что применение методов обучения с подкреплением позволило достичь коэффициента Шарпа в 0.483 в условиях высокой волатильности рынка. Данный показатель свидетельствует об эффективности разработанного подхода в максимизации стоимости портфеля при одновременном снижении необходимости регулярных взносов. В отличие от традиционных стратегий, данный алгоритм динамически адаптируется к изменяющимся рыночным условиям, позволяя инвесторам извлекать прибыль даже в периоды нестабильности. Фактически, представленный подход демонстрирует возможность получения конкурентоспособной доходности при минимизации финансовых обязательств, что делает его привлекательным решением для оптимизации инвестиционных стратегий. Полученный коэффициент Шарпа, $0.483$, указывает на высокую эффективность использования капитала и способность генерировать доходность, превышающую риски.

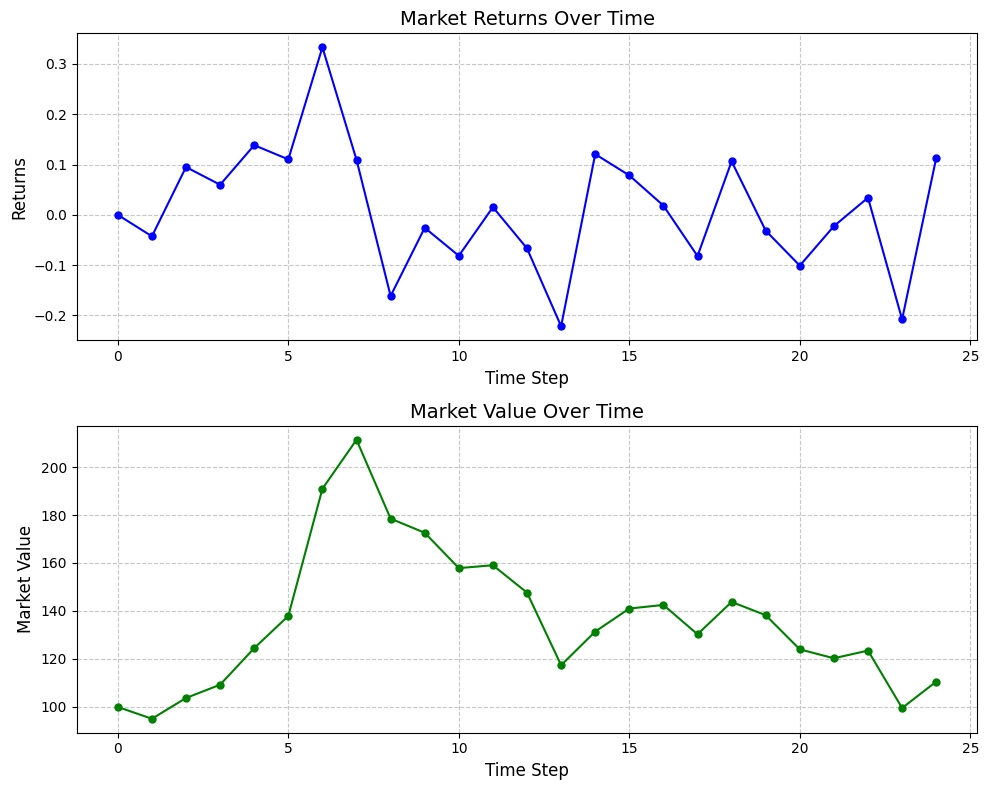
Динамика рыночной доходности и рыночной стоимости демонстрирует их взаимосвязь во времени.

Исследование демонстрирует, что оптимизация портфеля посредством обучения с подкреплением — это не поиск идеальной рациональной стратегии, а скорее попытка убедить себя в предсказуемости финансовых рынков. Алгоритм G-Learning, нацеленный на достижение конкретной финансовой цели в заданные сроки, напоминает о том, как человек создает сложные модели, чтобы уменьшить тревогу перед неопределенностью. Как заметил Поль Фейерабенд: “Любая гипотеза, которую мы выдвигаем, является лишь попыткой навязать миру свой порядок”. В данном случае, эта попытка выражается в стремлении максимизировать коэффициент Шарпа, игнорируя при этом всю сложность и иррациональность поведения участников рынка.

Что дальше?

Представленная работа демонстрирует, что алгоритмы обучения с подкреплением могут быть применены к оптимизации портфеля, и даже учитывать горизонт планирования. Однако, не стоит обольщаться. Человек — не рациональный агент, стремящийся к максимальной выгоде. Он выбирает не оптимум, а комфорт, и эта иррациональность сложно поддается формализации. Задача не в том, чтобы создать идеальный алгоритм, а в том, чтобы создать алгоритм, который достаточно хорошо справляется с человеческой непредсказуемостью.

Очевидным следующим шагом представляется интеграция поведенческих моделей в процесс обучения. Необходимо учитывать склонность к избеганию потерь, эффект привязки, и другие когнитивные искажения, которые влияют на инвестиционные решения. Возможно, стоит отойти от максимизации коэффициента Шарпа и сосредоточиться на минимизации тревожности инвестора — ведь мы не ищем выгоду, а ищем уверенность.

В конечном счете, успех подобных исследований будет зависеть не от сложности математического аппарата, а от глубины понимания человеческой психологии. Алгоритмы могут быть эффективными, но они всегда будут лишь упрощением сложной реальности, в которой доминируют надежды, страхи и привычки, а не холодный расчет.

Оригинал статьи: https://arxiv.org/pdf/2511.18076.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-25 21:28