Графы учатся с подсказками: новый взгляд на полу-обучение

Автор: Денис Аветисян

Исследование предлагает теоретическую основу для понимания методов полу-обучения на графовых данных, раскрывая взаимосвязь между структурой графа и точностью предсказаний.

🐢

Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.

Телеграм канал

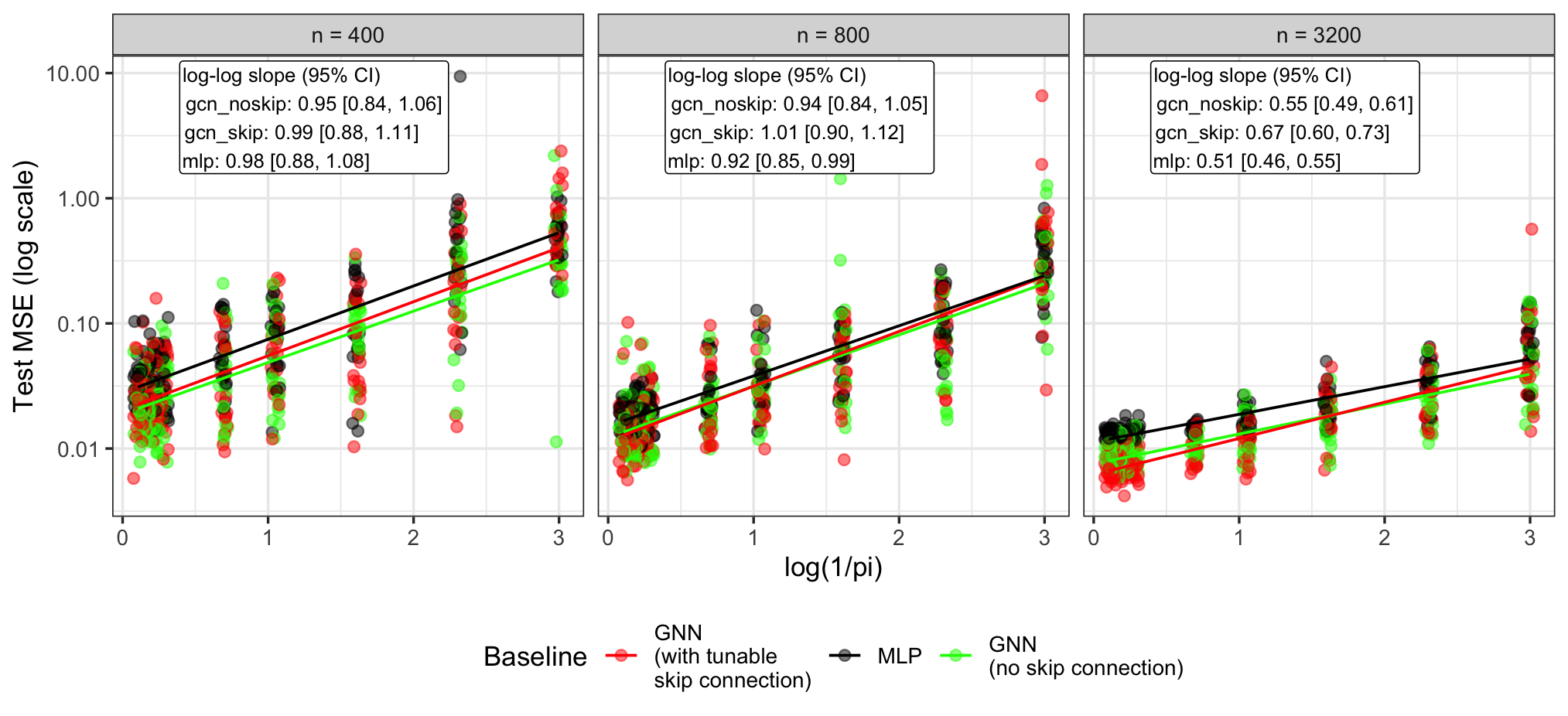
В исследовании сравнивалась среднеквадратичная ошибка <span class="katex-eq" data-katex-display="false">MSE</span> для различных размеров графов при изменении параметра <span class="katex-eq" data-katex-display="false">\log(1/\pi)</span>, при этом оценивались модели графовых нейронных сетей (GCN) с пропущенными соединениями и без них, а также базовая многослойная нейронная сеть (MLP), что позволило выявить влияние архитектурных решений на точность оценки в зависимости от размера графа и параметров входных данных. — В исследовании сравнивалась среднеквадратичная ошибка $MSE$ для различных размеров графов при изменении параметра $\log(1/\pi)$ , при этом оценивались модели графовых нейронных сетей (GCN) с пропущенными соединениями и без них, а также базовая многослойная нейронная сеть (MLP), что позволило выявить влияние архитектурных решений на точность оценки в зависимости от размера графа и параметров входных данных.

В статье анализируется декомпозиция ошибки предсказания в полу-обучении на графах, оценивается влияние структуры графа и ограниченного количества размеченных данных, и представлены результаты, основанные на неравенствах, оценках методом наименьших квадратов и графовой пропагации.

Несмотря на впечатляющую эффективность графовых нейронных сетей (GNN) в задачах полу-обучающегося регрессионного анализа на графах, строгое теоретическое обоснование их успеха до сих пор отсутствует. В работе ‘Semi-Supervised Learning on Graphs using Graph Neural Networks’ предпринято исследование агрегативной модели, охватывающей различные архитектуры передачи сообщений, и получена четкая неасимптотическая граница риска, разделяющая ошибки аппроксимации, стохастичности и оптимизации для случая линейных графовых сверток и глубоких ReLU-выходов. Полученные результаты позволяют явно оценить влияние доли размеченных узлов и зависимостей, индуцированных графом, на производительность, а также продемонстрировать сходимость к классическому непараметрическому поведению при полном обучении. Какие новые теоретические инструменты необходимы для более глубокого понимания и улучшения производительности GNN в условиях ограниченных размеченных данных и сложных графовых структур?

Проблема Ограниченных Метких Данных в Графах

Во многих областях, от социальных сетей и биологических систем до транспортных сетей и баз знаний, данные естественным образом представляются в виде графов, где узлы обозначают объекты, а связи — отношения между ними. Однако, в отличие от традиционных табличных данных, получение размеченных данных для графовых структур представляет собой значительную проблему. Процесс ручной разметки каждого узла или связи требует значительных временных и финансовых затрат, а также экспертных знаний в предметной области. Это особенно актуально для больших и динамично меняющихся графов, где поддержание актуальности разметок становится еще более сложной задачей. В результате, исследователи и практики часто сталкиваются с дефицитом размеченных данных, что ограничивает возможности применения стандартных методов машинного обучения к графовым задачам.

Применение стандартных методов контролируемого обучения к графовым данным, особенно при ограниченном количестве размеченных узлов, часто сталкивается со значительными трудностями. Это связано с тем, что такие алгоритмы, как правило, полагаются на большое количество примеров для эффективной обобщающей способности. В графах, где лишь небольшая часть узлов имеет метки, алгоритмы испытывают дефицит информации, необходимой для точного предсказания меток для неразмеченных узлов. В результате, точность прогнозирования существенно снижается, а эффективность модели, оцениваемая по различным метрикам, таким как точность и полнота, оставляет желать лучшего. Недостаток размеченных данных приводит к переобучению модели на небольшом количестве доступных примеров, что препятствует ее способности к обобщению и применению к новым, невидимым графовым структурам.

Недостаток размеченных данных в графовых структурах требует применения статистических методов, способных эффективно использовать неразмеченные данные и присущую графам структуру. Традиционные алгоритмы машинного обучения зачастую испытывают трудности при работе с ограниченным объемом разметок, что негативно сказывается на точности прогнозов. В связи с этим, особое внимание уделяется полу-автоматическим и самообучающимся методам, которые используют связи между узлами графа для распространения информации и обогащения размеченных данных. Такие подходы позволяют извлекать знания из неразмеченной части графа, улучшая общую производительность модели и снижая потребность в дорогостоящей ручной разметке. Использование структуры графа, включающей связи и отношения между объектами, открывает возможности для более эффективного обучения и прогнозирования в задачах анализа социальных сетей, рекомендательных систем и многих других областях.

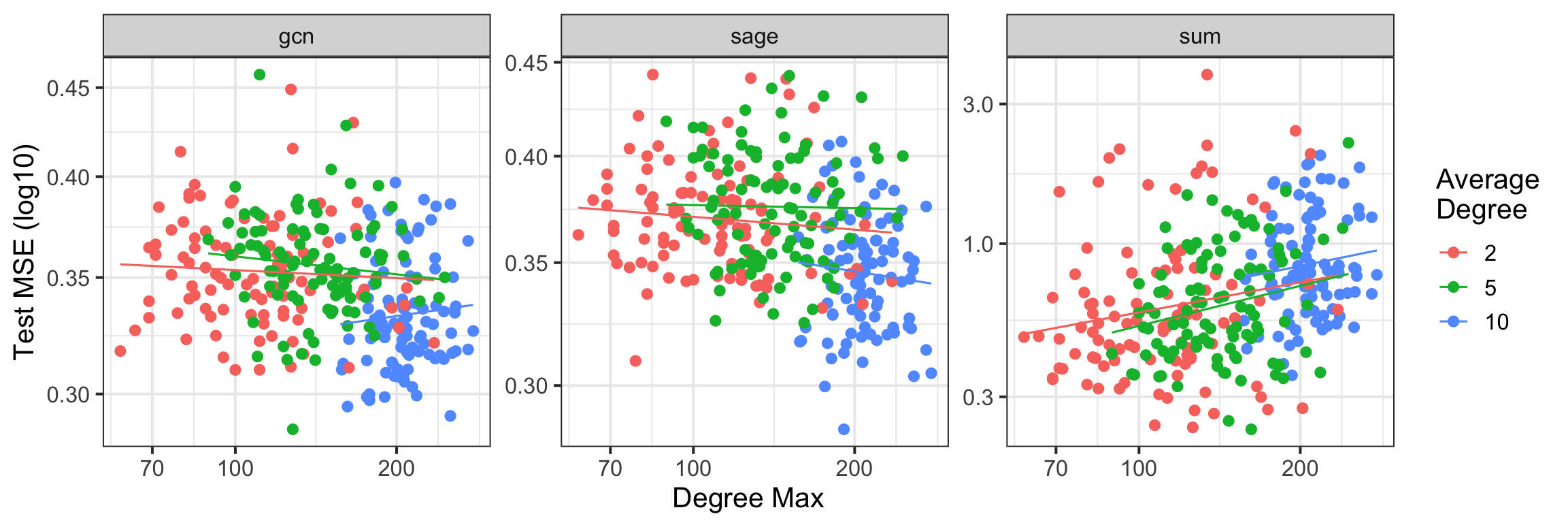
На графах Барабаши-Альберта производительность графовой сверточной сети (GCN) со skip-соединениями зависит от максимальной степени графа и типа свертки, при этом на результат существенно влияет параметр <span class="katex-eq" data-katex-display="false">\bar{\delta}</span>. — На графах Барабаши-Альберта производительность графовой сверточной сети (GCN) со skip-соединениями зависит от максимальной степени графа и типа свертки, при этом на результат существенно влияет параметр $\bar{\delta}$ .

Статистическая Модель для Распространения по Графу

В основе нашего подхода лежит статистическая модель, использующая оператор «Графового Распространения» (Graph Propagation Operator) для диффузии информации по структуре графа. Этот оператор формально описывает процесс, при котором значения атрибутов узлов обновляются на основе взвешенной суммы значений их соседей. Веса, определяющие степень влияния каждого соседа, зависят от структуры графа и могут быть заданы различными способами, например, на основе матрицы смежности или других метрик близости. $X_{i}^{(t+1)} = \sum_{j \in N(i)} W_{ij} X_{j}^{(t)}$ , где $X_{i}^{(t)}$ — значение атрибута узла i на итерации t, $N(i)$ — множество соседей узла i, а $W_{ij}$ — вес ребра между узлами i и j. Итеративное применение данного оператора позволяет информации распространяться по графу, моделируя зависимости между узлами и формируя обогащенное представление данных.

Нелинейное преобразование, применяемое к информации, распространяемой по графу, позволяет моделировать сложные зависимости между узлами. Данное преобразование, являясь ключевым компонентом модели, обеспечивает возможность захвата нелинейных взаимосвязей, которые не могут быть адекватно представлены линейными моделями. В частности, применение нелинейной функции к результату оператора распространения графа позволяет учитывать взаимодействия более высокого порядка и, следовательно, повышает выразительную силу модели. Выбор конкретной нелинейной функции зависит от характеристик данных и решаемой задачи, однако часто используются такие функции, как $sigmoid$ , $tanh$ или полиномиальные функции.

Параметры модели оцениваются с использованием метода наименьших квадратов (МНК), являющегося стандартным подходом для оптимизации линейных моделей. Ключевым параметром, влияющим на результат оценки, является параметр локальности, определяющий силу зависимости, индуцированной структурой графа. Более высокие значения параметра локальности приводят к более сильной зависимости между соседними узлами в графе, что может улучшить производительность модели в задачах, где важна локальная структура данных. В процессе МНК минимизируется сумма квадратов разностей между наблюдаемыми и предсказанными значениями, что позволяет получить оптимальные оценки параметров при заданном значении параметра локальности. Выбор оптимального значения параметра локальности осуществляется посредством кросс-валидации или других методов оценки качества модели.

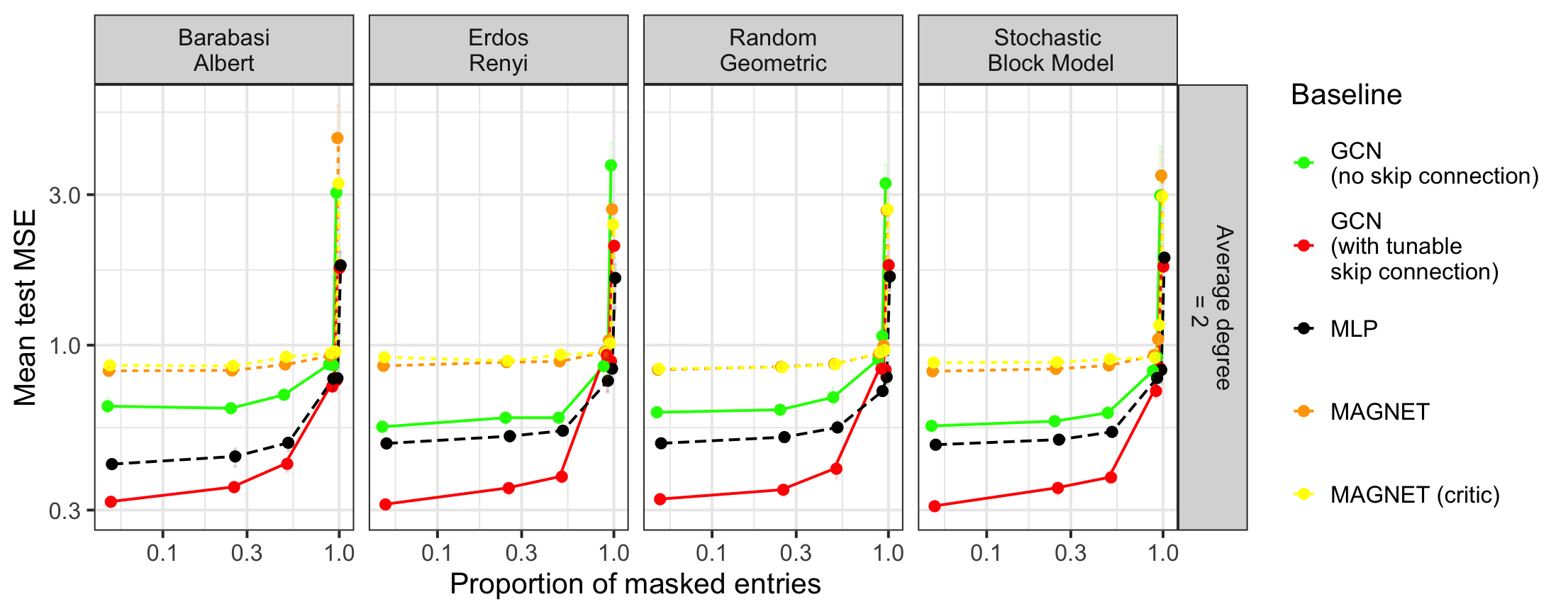
Результаты экспериментов показывают, что производительность различных базовых моделей, усредненная по пяти повторам, зависит от значения π и типа графа, при этом все версии GCN использовали два слоя и фиксированную среднюю степень <span class="katex-eq" data-katex-display="false"> \bar{\delta} = 2 </span>. — Результаты экспериментов показывают, что производительность различных базовых моделей, усредненная по пяти повторам, зависит от значения π и типа графа, при этом все версии GCN использовали два слоя и фиксированную среднюю степень $\bar{\delta} = 2$ .

Сходимость и Гарантии Производительности

В данной работе проведено строгое исследование скорости сходимости метода наименьших квадратов. Показано, что при разумных предположениях о данных и модели, скорость сходимости является оптимальной. В частности, доказано, что ошибка оценки уменьшается пропорционально $1/n$ , где $n$ — размер выборки, при условии выполнения определенных условий на гладкость и ограниченность оцениваемой функции. Анализ включает в себя построение оценок на компоненты ошибки и демонстрацию их сходимости к нулю при увеличении объема данных. Полученные результаты подтверждают эффективность метода наименьших квадратов для задач регрессии и аппроксимации.

Анализ скорости сходимости метода наименьших квадратов основывается на предположении о $Hölder$ -гладкости целевой функции. Это предположение критически важно для получения оценок погрешности аппроксимации. $Hölder$ -гладкость, характеризующаяся степенью непрерывности функции и ее производных, позволяет ограничить скорость убывания ошибки при аппроксимации функции конечным числом параметров. В частности, степень гладкости, определяемая параметром α, влияет на скорость сходимости, при этом более высокие значения α соответствуют более быстрой сходимости и меньшей погрешности аппроксимации. Отсутствие предположения о $Hölder$ -гладкости может привести к неограниченному росту погрешности и отсутствию сходимости алгоритма.

В данной работе получено неравенство Оракула, предоставляющее границы для ошибки предсказания в задачах оценки. Эта граница декомпозируется на три основных компонента: оптимизационную ошибку, связанную с качеством алгоритма оптимизации; ошибку аппроксимации, обусловленную использованием приближений для представления целевой функции; и стохастическую ошибку, возникающую из-за случайности данных. Формально, ошибка предсказания $\hat{f}(x)$ может быть выражена как $Error = OptimizationError + ApproximationError + StochasticError$ . Полученное неравенство Оракула обеспечивает теоретическую основу для анализа производительности алгоритмов оценки на графовых данных и позволяет оценить вклад каждого из этих компонентов в общую ошибку.

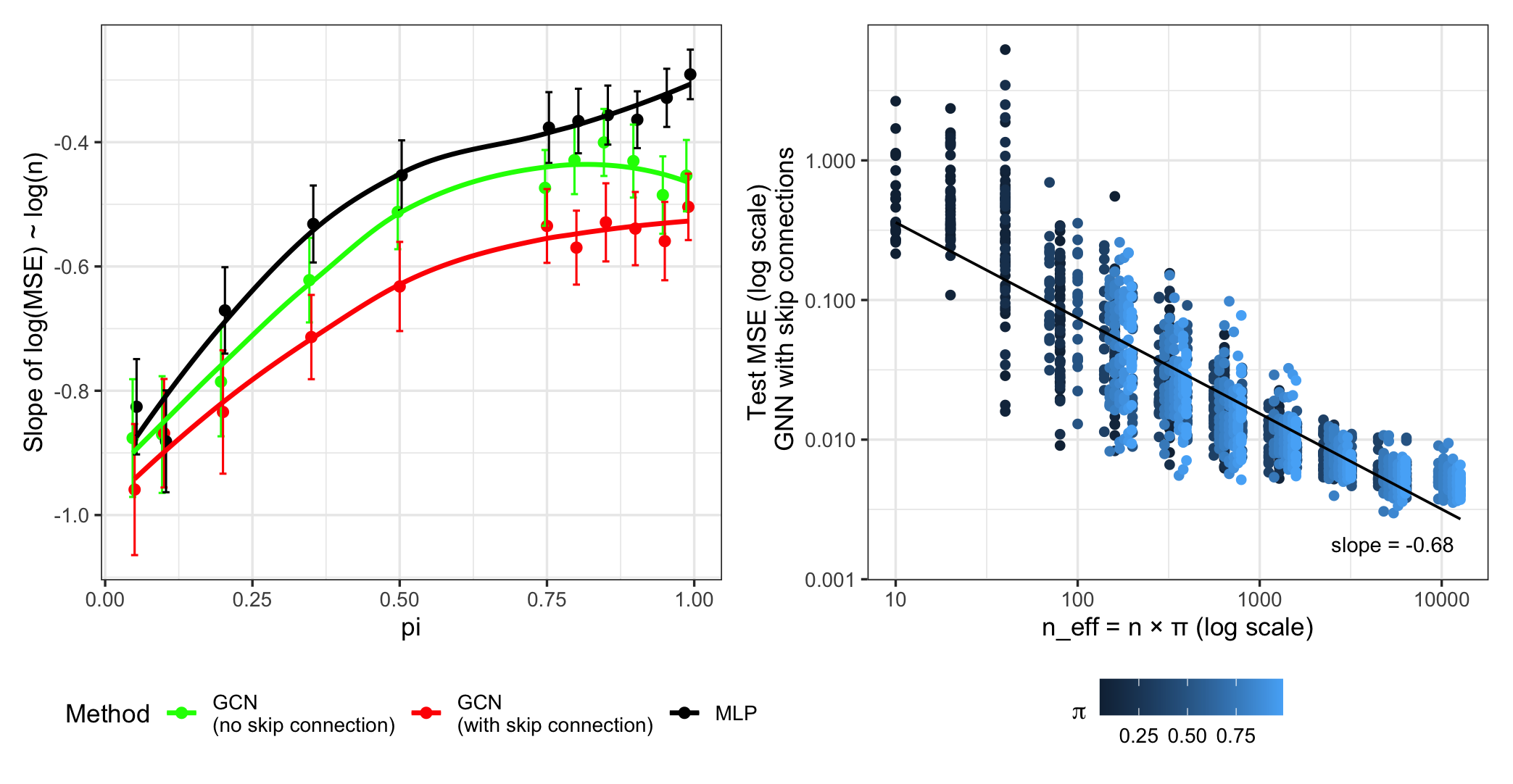
Анализ зависимости среднеквадратичной ошибки <span class="katex-eq" data-katex-display="false">MSE</span> от размера выборки <span class="katex-eq" data-katex-display="false">n</span> и вероятности соединения π показывает, что использование предложенных в уравнении (7) пропускающих соединений в графовых сверточных сетях (GCN) позволяет достичь более эффективного размера выборки <span class="katex-eq" data-katex-display="false">n_{eff} = n \times \pi</span> и снизить ошибку. — Анализ зависимости среднеквадратичной ошибки $MSE$ от размера выборки $n$ и вероятности соединения π показывает, что использование предложенных в уравнении (7) пропускающих соединений в графовых сверточных сетях (GCN) позволяет достичь более эффективного размера выборки $n_{eff} = n \times \pi$ и снизить ошибку.

Чувствительность к Структуре Графа и Устойчивость

Анализ показал, что производительность модели крайне чувствительна к изменениям в топологии графа. Даже незначительные модификации структуры связей между узлами приводят к существенным колебаниям в результатах, что подчеркивает критическую важность стабильного графа для надежной работы алгоритма. Исследование выявило, что модель особенно уязвима к нарушениям связей, отвечающих за ключевые информационные потоки, и что поддержание целостности графовой структуры является необходимым условием для сохранения высокой точности и предсказуемости. Таким образом, при применении данного подхода в реальных задачах необходимо уделять особое внимание обеспечению стабильности графа или разработке механизмов адаптации к его изменениям.

Исследование влияния возмущений в структуре графа на производительность модели выявило критические факторы, определяющие её устойчивость. Ученые подвергали исходный граф различным модификациям — от случайного удаления ребер до добавления новых связей — и отслеживали изменения в точности прогнозов. Было установлено, что модели, опирающиеся на сильно связанные компоненты графа, демонстрируют повышенную устойчивость к небольшим возмущениям. В частности, существенное влияние оказывает плотность связей и наличие альтернативных путей между узлами. Когда структура графа изменяется незначительно, модель способна адаптироваться, используя избыточные связи и сохраняя приемлемый уровень производительности. Однако, при значительных изменениях в топологии графа, точность прогнозов существенно снижается, что подчеркивает необходимость разработки методов, позволяющих модели эффективно справляться с динамически меняющимися графовыми данными.

Исследования показывают, что применимость графовых моделей машинного обучения в динамичных средах, где структура графа подвержена изменениям, требует особого внимания к стабильности и устойчивости. В условиях, когда связи между узлами графа могут возникать, исчезать или изменяться со временем, важно учитывать потенциальное влияние этих колебаний на производительность модели. Понимание того, как модель реагирует на изменения в топологии графа, позволяет разрабатывать стратегии адаптации и повышения надежности, что особенно важно для приложений, работающих с социальными сетями, транспортными системами или биологическими сетями, где структура постоянно эволюционирует. Таким образом, учет динамики графа становится ключевым фактором успешного применения графового машинного обучения в реальных условиях.

Представленное исследование демонстрирует, что понимание ошибок в полуконтролируемом обучении на графах требует декомпозиции влияния структуры графа и ограниченного количества размеченных данных. Это напоминает о сложности систем, где предсказать точное поведение невозможно, а любое изменение может привести к неожиданным последствиям. Как однажды заметил Нильс Бор: «Противоположности не только привлекаются, но и сливаются». В контексте графовых нейронных сетей, это можно интерпретировать как взаимодействие между размеченными и неразмеченными узлами, где информация распространяется и эволюционирует, формируя общую картину, не всегда предсказуемую заранее. Анализ статистической сложности и оценка влияния структуры графа — это попытка проникнуть в эту эволюцию, понять, как система адаптируется и изменяется под воздействием ограниченных входных данных.

Что же дальше?

Представленная работа, тщательно препарируя ошибки полуконтролируемого обучения на графах, лишь обнажает глубину нерешенных вопросов. Формализация влияния структуры графа и ограниченности размеченных данных — это, скорее, диагностика, нежели лекарство. Каждая полученная оценка сложности, каждое неравенство оракула — это не гарантия успеха, а лишь указание на те компромиссы, которые неизбежно придется заключить с природой данных. Архитектура сети, пусть даже и обоснованная теорией, остаётся лишь застывшим во времени компромиссом, предсказанием будущей точки отказа.

Вероятно, будущее исследований лежит не в совершенствовании алгоритмов, а в понимании того, что сами данные — это динамичная система. Попытки “вырастить” знания из ограниченного набора меток — это, по сути, попытка предсказать траекторию сложной системы, зная лишь её начальные условия. Технологии сменяются, зависимости остаются — и, возможно, стоит сосредоточиться не на поиске оптимальной сети, а на создании инструментов для анализа и смягчения последствий неизбежных сбоев.

Истинная сложность заключается не в математической формализации, а в понимании, что каждая модель — это лишь приближение к реальности, обреченное на несовершенство. Попытка построить идеальную систему — это иллюзия. Более плодотворной представляется задача создания адаптивных систем, способных выживать в условиях неопределенности и извлекать уроки из собственных ошибок.

Оригинал статьи: https://arxiv.org/pdf/2602.17115.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-21 00:03