Граф ближайших соседей: ускорение классификации без потери точности

Автор: Денис Аветисян

Новая модель kkNN-Graph позволяет значительно повысить скорость алгоритма k-Nearest Neighbors, сохраняя при этом высокую точность классификации.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал

Адаптивная модель графов для kNN, в отличие от традиционного подхода с фиксированным значением k и затратным поиском ближайших соседей, динамически формирует оптимальную структуру окрестностей для каждого образца, учитывая локальную плотность данных, и внедряет предварительно вычисленную метку консенсуса непосредственно в каждый узел, что позволяет при классификации использовать иерархическую структуру «Малый мир» (HNSW) для быстрого доступа к ближайшему узлу и мгновенного получения его метки, обеспечивая логарифмическое время классификации без необходимости проведения голосования в реальном времени.

Предложена адаптивная графовая модель для приближенного поиска ближайших соседей, использующая иерархический индекс и разреженное представление данных.

Несмотря на широкое применение алгоритма k-ближайших соседей (kNN) в задачах классификации, его масштабирование на больших объемах данных остается сложной задачей из-за вычислительных затрат. В данной работе, представленной под названием ‘kNN-Graph: An adaptive graph model for $k$-nearest neighbors’, предлагается новый подход, использующий адаптивную графовую модель для существенного ускорения процесса классификации. Ключевым нововведением является предварительное вычисление границ принятия решений и применение иерархического графового индекса, что позволяет достичь высокой скорости работы без потери точности. Возможно ли, используя предложенную архитектуру, создать принципиально новые парадигмы непараметрического обучения, основанные на графовых представлениях данных?

Проклятие Размерности: Вызов для Алгоритмов Ближайших Соседей

Во многих задачах машинного обучения, таких как классификация, кластеризация и поиск по подобию, ключевым этапом является эффективное определение ближайших соседей для заданного объекта. Однако, с увеличением размерности пространства признаков, эта задача становится чрезвычайно сложной. Феномен, известный как «проклятие размерности», приводит к тому, что расстояние между точками в высокоразмерном пространстве стремится к одному и тому же значению, что затрудняет точное определение ближайших соседей и существенно снижает производительность алгоритмов. В результате, традиционные методы поиска ближайших соседей, которые хорошо работают в пространствах небольшой размерности, становятся неэффективными и требуют экспоненциального увеличения вычислительных ресурсов при увеличении числа признаков, что ограничивает их применимость к реальным задачам с большими объемами данных и высокой размерностью.

Традиционные алгоритмы поиска ближайших соседей, такие как KD-деревья и метод полного перебора, сталкиваются с серьезными ограничениями при работе с большими объемами данных и высокой размерностью пространства признаков. По мере увеличения количества измерений, эффективность KD-деревьев резко падает из-за “проклятия размерности”, когда пространство поиска становится разреженным, а глубина дерева растет экспоненциально. Метод полного перебора, хотя и гарантирует нахождение точного ближайшего соседа, требует вычисления расстояния до каждой точки в наборе данных, что приводит к квадратичной сложности $O(n)$ , делая его неприменимым для масштабных задач. В результате, время поиска увеличивается непропорционально росту объема данных, что делает использование этих методов непрактичным для современных приложений, требующих высокой скорости обработки и масштабируемости, таких как системы рекомендаций и анализ изображений.

Возникающие вычислительные трудности существенно ограничивают возможности применения алгоритмов поиска ближайших соседей в ряде важных областей. В частности, системы распознавания изображений сталкиваются с задержками при поиске схожих визуальных паттернов в больших базах данных, что влияет на скорость и точность идентификации объектов. Рекомендательные системы, полагающиеся на выявление пользователей со схожими предпочтениями, испытывают проблемы с масштабируемостью и оперативностью предоставления персонализированных предложений. Кроме того, задачи обнаружения аномалий, требующие быстрой идентификации необычных данных, становятся неэффективными при увеличении размерности пространства признаков, что снижает надежность систем безопасности и мониторинга. Таким образом, преодоление данного вычислительного барьера является ключевым фактором для развития и внедрения интеллектуальных систем в различных сферах.

Суть проблемы поиска ближайших соседей в многомерных пространствах заключается в сложном балансе между точностью результатов, вычислительной сложностью и скоростью получения ответа. По мере увеличения размерности данных, традиционные алгоритмы сталкиваются с “проклятием размерности”, когда расстояние между точками становится более однородным, что снижает эффективность поиска. Сохранение высокой точности требует перебора все большего числа кандидатов, что приводит к экспоненциальному росту вычислительных затрат. В результате, возникает необходимость разработки методов, которые способны находить приближенные ближайшие соседи за приемлемое время, жертвуя незначительной частью точности ради значительного увеличения скорости работы, особенно при обработке больших объемов данных в задачах распознавания образов, рекомендательных системах и обнаружении аномалий.

Анализ отмены показал, что адаптивное обучение окрестностей значительно повышает дискриминационную способность модели, что подтверждается улучшением метрик классификации (точность, точность, полнота и F1-мера) по шести эталонным наборам данных, благодаря совместной оптимизации количества и весов соседей.

За Пределами Деревьев: Исследуем Приближенные Методы Ближайших Соседей

Локально-чувствительное хеширование (LSH) представляет собой вероятностный метод поиска ближайших соседей, основанный на использовании хеш-функций, которые с большей вероятностью сопоставляют близкие векторы в одинаковые хеш-корзины. Однако эффективность LSH напрямую зависит от тщательной настройки параметров, таких как количество хеш-функций и размер хеш-корзин. Неправильная настройка может привести к высокому числу ложных срабатываний — возврату векторов, которые не являются истинными ближайшими соседями. Вероятностная природа метода означает, что поиск может потребовать многократных проходов для достижения приемлемой точности, что влияет на производительность и вычислительные затраты.

Квантование произведений (Product Quantization) представляет собой метод, основанный на векторной квантизации, позволяющий эффективно снизить размерность данных. Алгоритм разделяет исходное векторное пространство на подпространства меньшей размерности, а затем для каждого подпространства строится кодовая книга, содержащая центроиды кластеров. Векторы кодируются индексами центроидов, к которым они ближе всего в соответствующих подпространствах. Неизбежно, процесс квантования приводит к потере информации, поскольку векторы заменяются их ближайшими представителями в кодовой книге, что может снизить точность поиска ближайших соседей. Степень потери информации напрямую зависит от размера кодовой книги и количества подпространств.

Несмотря на то, что методы, такие как локально-чувствительное хеширование и квантование произведений, демонстрируют улучшения в скорости поиска ближайших соседей, они часто не достигают оптимального баланса между точностью и эффективностью. Локально-чувствительное хеширование требует тщательной настройки параметров для минимизации ложных срабатываний, а квантование произведений, хотя и снижает размерность векторов, неизбежно приводит к потере информации. В результате, повышение скорости часто достигается за счет снижения точности результатов, что делает выбор между этими методами компромиссом, зависящим от конкретных требований приложения и допустимого уровня погрешности.

Необходимость в надежном и адаптируемом подходе к поиску ближайших соседей обуславливает развитие методов, основанных на графах. В отличие от методов, требующих точного вычисления расстояний до всех точек, графовые методы строят индекс в виде графа, где узлы представляют векторы, а ребра — связи между ближайшими соседями. Такой подход позволяет значительно сократить время поиска, особенно в высокоразмерных пространствах, за счет обхода только части графа. Адаптивность обеспечивается динамическим построением и обновлением графа, позволяющим эффективно обрабатывать новые данные и изменяющиеся запросы, что делает графовые методы перспективным направлением в задачах поиска ближайших соседей.

Предложенный фреймворк kkNN-Graph, состоящий из этапов обучения самовыражения в ядре, построения графа HNSW и инференса, позволяет эффективно классифицировать данные, находя ближайших соседей в ядре и используя их для взвешенного голосования, что обеспечивает высокую скорость и точность.

kkNN-Graph: Адаптивный Графовый Подход к Ближайшим Соседям

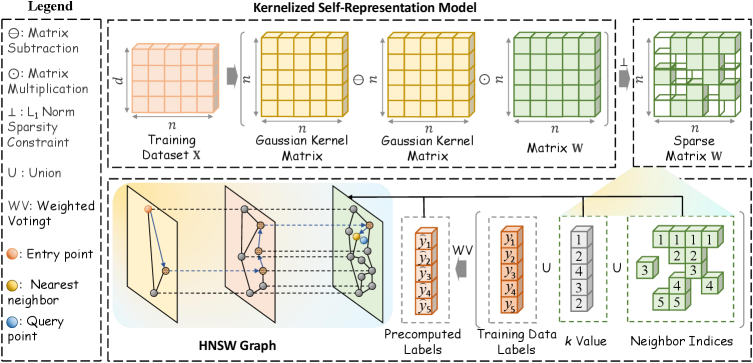
Модель kkNN-Graph представляет собой адаптивный графовый подход, динамически подстраивающийся под распределение данных. В отличие от традиционных методов поиска ближайших соседей, kkNN-Graph не использует фиксированное число соседей или предопределенные критерии отбора. Вместо этого, структура графа и веса ребер формируются непосредственно на основе локальной плотности данных и взаимосвязей между образцами. Это позволяет эффективно оптимизировать процесс поиска ближайших соседей, обеспечивая высокую точность и скорость работы, особенно в задачах с высокой размерностью и сложными данными. Адаптивность модели достигается за счет использования методов обучения, которые позволяют выявлять и учитывать изменения в распределении данных, автоматически корректируя структуру графа для поддержания оптимальной производительности.

Модель kkNN-Graph использует адаптивное обучение соседству и ядро самопредставления для определения оптимального количества и весов соседей для каждого образца данных. Адаптивное обучение соседству позволяет динамически изменять размер окрестности каждого образца в зависимости от локальной плотности данных, что позволяет избежать как слишком широких, так и слишком узких окрестностей. Ядро самопредставления, в свою очередь, позволяет выразить каждый образец как линейную комбинацию других образцов, причем веса этой комбинации определяются с использованием метода наименьших квадратов с $ℓ_1$ -регуляризацией. Это обеспечивает компактное представление данных и способствует эффективному определению наиболее релевантных соседей, учитывая их относительную важность в локальном пространстве признаков.

Ключевым элементом подхода kkNN-Graph является введение ограничения разреженности, реализуемого посредством $ℓ_1$ -нормы. Данное ограничение стимулирует создание компактных и эффективных представлений данных, отбирая наиболее значимые связи между образцами и обнуляя веса незначимых. Использование $ℓ_1$ -нормы приводит к формированию разреженных векторов весов соседства, что снижает вычислительные затраты и объем памяти, необходимые для хранения графа ближайших соседей. Это особенно важно при работе с высокоразмерными данными, где плотность связей между образцами обычно низка, а разреженность позволяет существенно улучшить производительность алгоритма.

Подход kkNN-Graph эффективно снижает влияние «проклятия размерности» за счет адаптивной структуры графа и использования разреженных представлений. В традиционных алгоритмах поиска ближайших соседей, увеличение числа измерений приводит к экспоненциальному росту вычислительной сложности и снижению точности. kkNN-Graph, используя ограничение разреженности, реализуемое через $ℓ_1$ -норму, формирует компактные представления данных, уменьшая потребность в полном переборе. Это значительно снижает вычислительную сложность поиска, позволяя осуществлять быстрый вывод и повышая эффективность алгоритма при работе с высокоразмерными данными. По сравнению с методами, не учитывающими размерность, kkNN-Graph демонстрирует существенное улучшение скорости поиска и сохранение точности даже при значительном увеличении числа признаков.

Предложенный метод демонстрирует сходимость целевой функции в процессе итераций на шести стандартных наборах данных.

Валидация и Усиление Производительности с kkNN-Graph

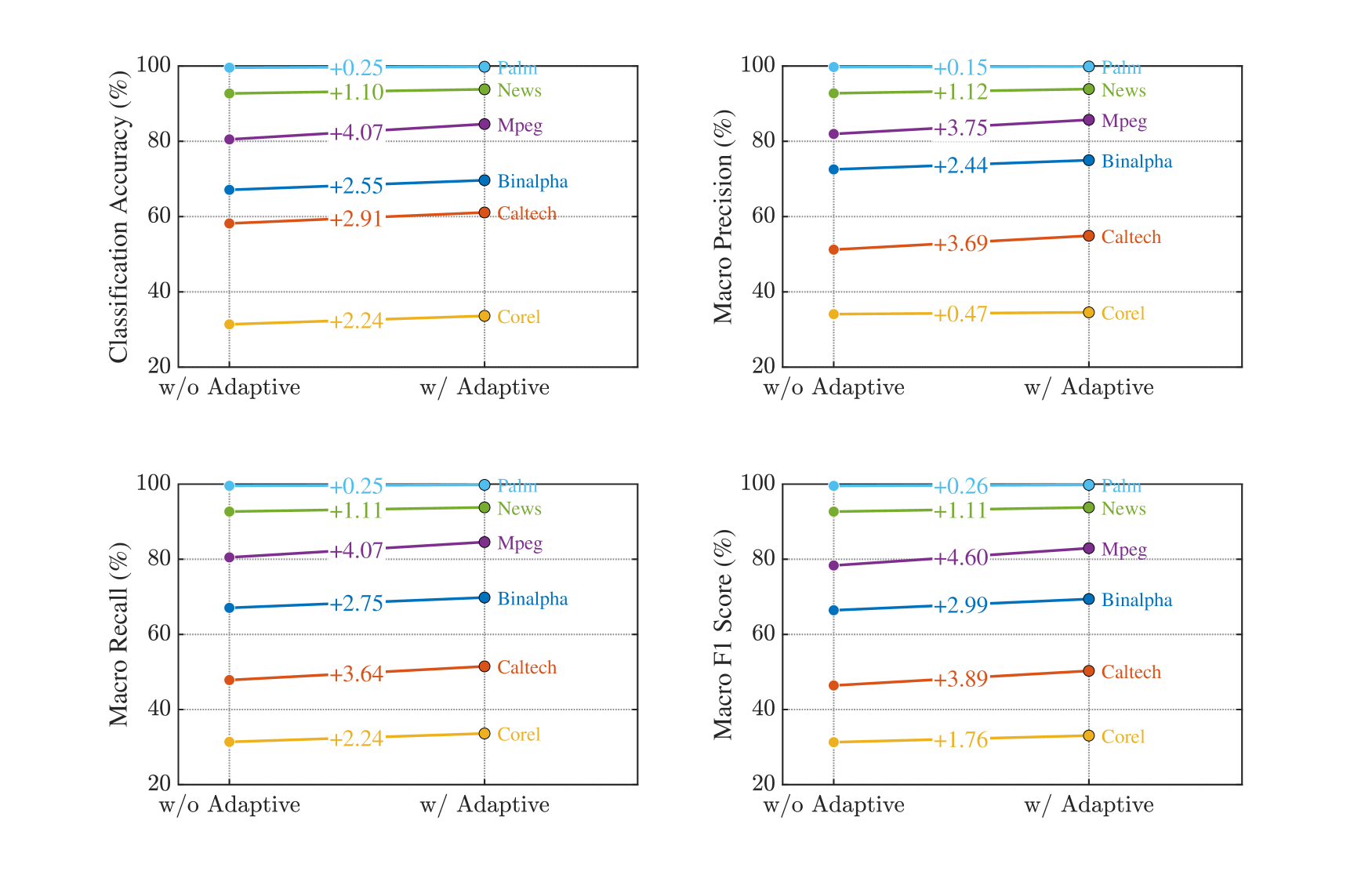
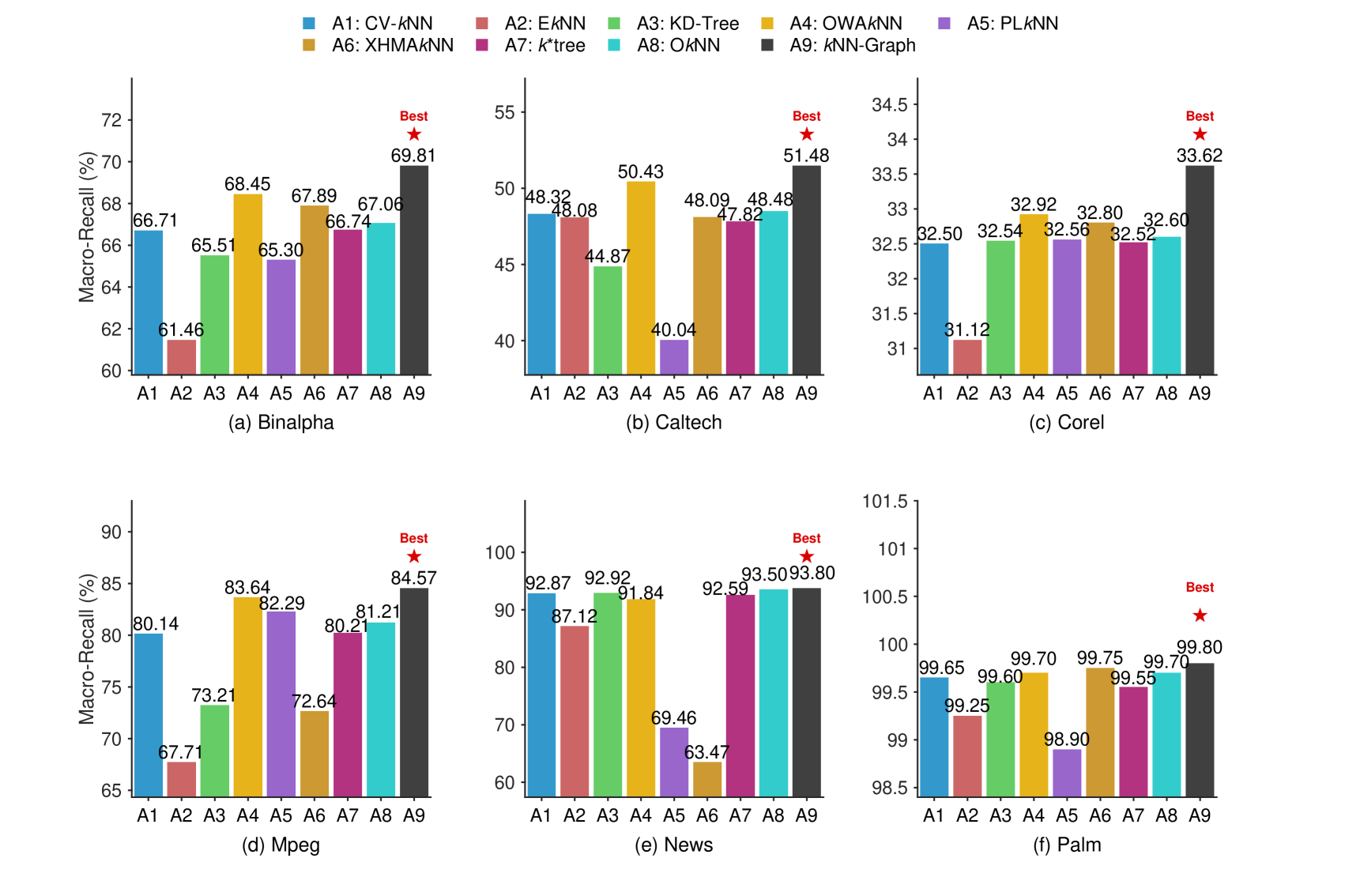
Экспериментальные исследования показали, что модель kkNN-Graph демонстрирует стабильно более высокую точность классификации по сравнению с традиционными методами. Средняя точность на шести различных наборах данных составила 73.76%. Данный результат подтверждает эффективность предложенного подхода к задаче классификации и указывает на превосходство kkNN-Graph в обработке разнообразных типов данных.

Для повышения точности классификации в kkNN-Graph используются методы EkkNN (Extended k-Nearest Neighbors) и OkkNN (Optimized k-Nearest Neighbors), которые совершенствуют процесс выбора ближайших соседей. EkkNN расширяет набор соседей, учитывая объекты, находящиеся на большем расстоянии, но имеющие схожие характеристики, что позволяет более эффективно обрабатывать сложные данные. OkkNN, в свою очередь, оптимизирует процесс выбора, отсеивая менее релевантные объекты и сосредотачиваясь на наиболее информативных соседях. Комбинированное применение этих техник позволяет более точно определить принадлежность объекта к определенному классу, повышая общую производительность модели и ее устойчивость к шумам в данных.

В основе kkNN-Graph лежит структура графа HNSW (Hierarchical Navigable Small World), обеспечивающая эффективный поиск ближайших соседей. HNSW использует многоуровневую иерархию графов с уменьшающимся числом узлов на каждом уровне, что позволяет значительно сократить время поиска. В процессе поиска алгоритм начинает с верхнего уровня и быстро перемещается к наиболее перспективным узлам, постепенно спускаясь на более низкие уровни для уточнения результатов. Такая структура обеспечивает логарифмическую сложность поиска, что критически важно для больших наборов данных и ускоряет процесс классификации по сравнению с традиционными методами поиска ближайших соседей.

Эксперименты показали, что kkNN-Graph обеспечивает значительное ускорение инференса по сравнению с существующими методами. На датасете Caltech достигнуто ускорение до 55x, а на датасете News — более 6500x. При этом, модель демонстрирует стабильный результат по метрике Macro-F1 Score, достигающий значения 73.98%, что подтверждает высокую эффективность и точность предложенного подхода к классификации.

В среднем, по результатам десяти запусков на шести общедоступных наборах данных, алгоритмы демонстрируют схожий уровень Macro-Recall.

Будущие Направления и Более Широкое Влияние Адаптивных Ближайших Соседей

Структура kkNN-Graph представляет собой гибкую основу для решения широкого спектра задач машинного обучения. Её адаптивность позволяет эффективно применять её в различных областях, включая поиск изображений, где она обеспечивает быстрое и точное извлечение релевантных визуальных данных. В системах рекомендаций kkNN-Graph способна выявлять скрытые закономерности и предлагать персонализированные рекомендации пользователям, основываясь на сходстве предпочтений. Кроме того, данная структура демонстрирует высокую эффективность в задачах обнаружения аномалий, позволяя выявлять необычные или подозрительные данные, отклоняющиеся от нормального поведения. Благодаря своей универсальности и способности адаптироваться к различным типам данных, kkNN-Graph открывает новые возможности для разработки более интеллектуальных и эффективных систем машинного обучения.

В настоящее время исследования активно направлены на тонкую настройку параметров модели и поиск инновационных подходов к адаптивному выбору ближайших соседей. Ученые экспериментируют с различными функциями расстояния и стратегиями взвешивания соседей, стремясь повысить точность и устойчивость алгоритма в различных условиях. Особое внимание уделяется методам, позволяющим динамически изменять число соседей в зависимости от плотности данных и сложности задачи. Подобные усовершенствования позволяют адаптировать модель к конкретным требованиям приложения, обеспечивая оптимальный баланс между вычислительными затратами и качеством результатов. Разработка алгоритмов, способных эффективно определять наиболее релевантных соседей в многомерном пространстве, является ключевым направлением для дальнейшего развития адаптивных алгоритмов поиска ближайших соседей.

Разработка структуры kktree, адаптивной системы индексирования, представляет собой перспективное направление для повышения эффективности поиска в задачах машинного обучения. В отличие от традиционных деревьев, kktree динамически адаптируется к распределению данных, создавая более сбалансированную структуру и минимизируя время поиска. Этот подход особенно важен при работе с высокоразмерными данными, где стандартные методы индексирования становятся неэффективными из-за проклятия размерности. Благодаря способности kk*tree оптимизировать процесс поиска, алгоритмы, использующие эту структуру, демонстрируют значительное ускорение и повышенную масштабируемость, что открывает возможности для решения более сложных и ресурсоемких задач в области анализа данных и искусственного интеллекта.

Представленная работа демонстрирует принципиально новый подход к организации поиска ближайших соседей, позволяющий отделить вычислительную сложность алгоритма от размерности данных. Традиционно, увеличение количества признаков в данных приводит к экспоненциальному росту времени поиска, что существенно ограничивает применимость многих алгоритмов машинного обучения к высокоразмерным задачам. Однако, благодаря разработанному методу, вычислительные затраты остаются управляемыми даже при работе с очень большими объемами данных и высокой размерностью признакового пространства. Это открывает перспективы для создания более масштабируемых и эффективных систем машинного обучения, способных решать сложные задачи в различных областях, таких как анализ изображений, обработка естественного языка и рекомендательные системы. Возможность преодолеть ограничения, связанные с проклятием размерности, является важным шагом на пути к созданию интеллектуальных систем, способных эффективно обрабатывать и анализировать огромные массивы данных.

Исследование, представленное в данной работе, демонстрирует стремление к оптимизации классификации методом k-ближайших соседей посредством создания адаптивного графа kkNN. Этот подход, по сути, представляет собой попытку деконструкции традиционной дилеммы между скоростью и точностью. Как однажды заметил Г.Х. Харди: «Математика — это искусство делать точные выводы из неточных предпосылок». Подобно тому, как математик работает с неопределенностью, авторы статьи предлагают метод, позволяющий строить приближенные, но эффективные границы принятия решений. Использование иерархического графа и разреженного представления данных — это, по сути, попытка взломать систему, найти оптимальный путь к решению, минуя вычислительные ограничения. Данная работа, таким образом, подтверждает, что понимание системы — ключ к ее преодолению.

Куда же дальше?

Представленный подход к ускорению поиска ближайших соседей, хоть и элегантен в своей реализации, всё же обнажает фундаментальную проблему: любая предварительная обработка — это всегда компромисс. Создание и поддержание иерархического графа требует ресурсов, а адаптация к изменяющимся данным — это постоянная борьба с энтропией. Вопрос в том, насколько эффективно можно автоматизировать этот процесс, чтобы затраты на адаптацию не нивелировали выигрыш в скорости.

Интересно рассмотреть возможность использования kkNN-Graph не как самоцели, а как строительного блока для более сложных систем. Представьте, что граф не просто хранит информацию о ближайших соседях, но и активно участвует в процессе обучения, выявляя скрытые зависимости и аномалии. Это, в свою очередь, может привести к созданию самообучающихся систем классификации, способных адаптироваться к совершенно новым данным без необходимости полной перестройки графа.

И, конечно, стоит задуматься о масштабируемости. Современные наборы данных растут экспоненциально. Сможет ли kkNN-Graph эффективно работать с действительно огромными объемами информации, или же ему потребуются радикальные изменения в архитектуре и алгоритмах? Поиск ближайших соседей — это лишь частный случай более общей проблемы — поиска закономерностей в хаосе. И, возможно, решение этой проблемы лежит за пределами привычных нам методов.

Оригинал статьи: https://arxiv.org/pdf/2601.16509.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-27 02:24