Глубина энтропии: Искусственный интеллект на пути к пониманию голографического конуса

Автор: Денис Аветисян

Новое исследование демонстрирует возможности обучения с подкреплением для изучения голографического энтропийного конуса и выявления его скрытых структур.

🐢

Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.

Бесплатный Телеграм канал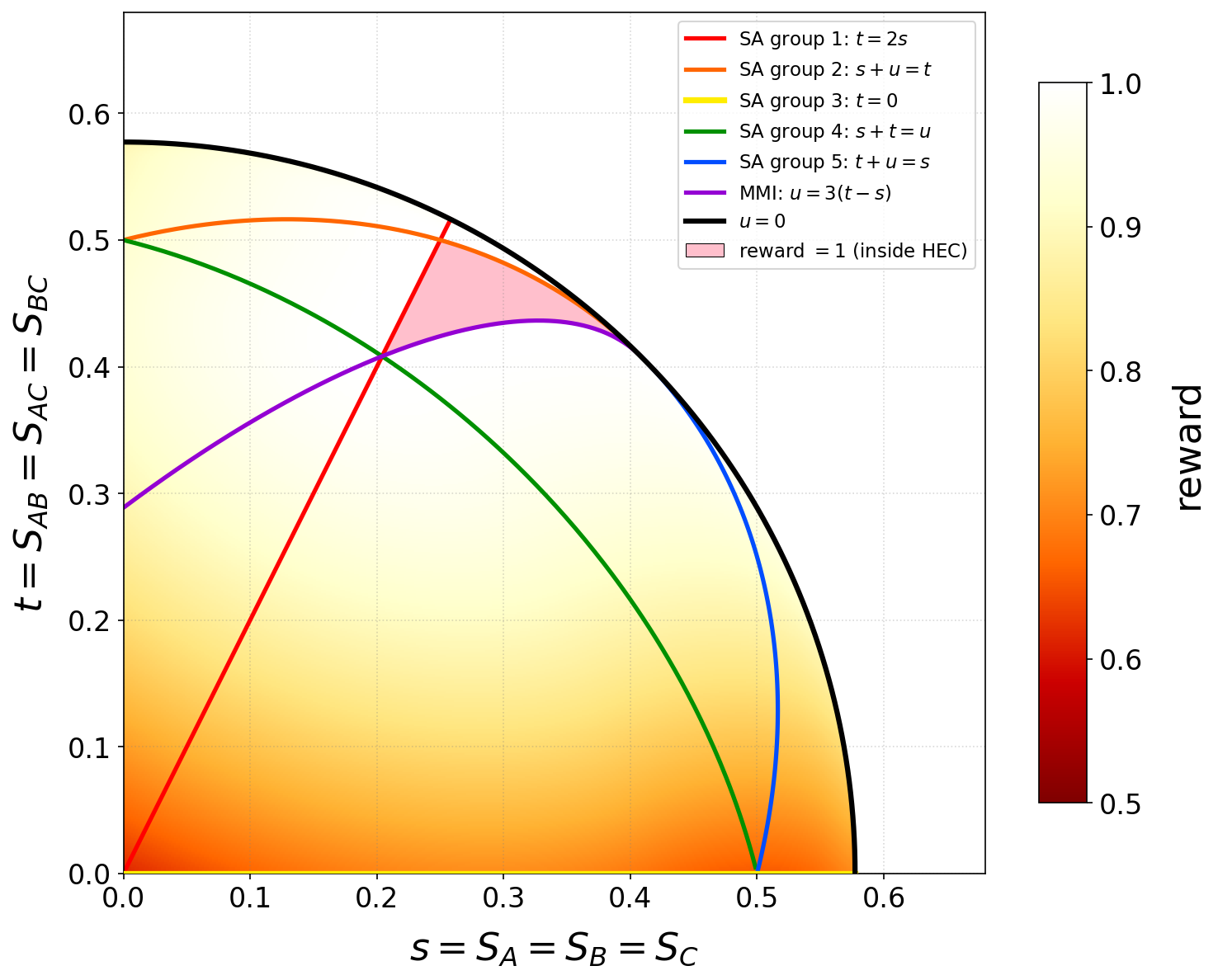

На симметричном сечении пространства энтропии <span class="katex-eq" data-katex-display="false">\mathcal{N}=3</span> в плоскости (s, t) аналитически вычисленная награда, соответствующая косинусной мере сходства, определяет ограничения для HEC (розовая область, <span class="katex-eq" data-katex-display="false">R=1</span>), обусловленные принципом максимальной информации (MMI), группой SA 1 и группой SA 2, при этом граница <span class="katex-eq" data-katex-display="false">u=0</span> служит пределом для данной области. — На симметричном сечении пространства энтропии $\mathcal{N}=3$ в плоскости (s, t) аналитически вычисленная награда, соответствующая косинусной мере сходства, определяет ограничения для HEC (розовая область, $R=1$ ), обусловленные принципом максимальной информации (MMI), группой SA 1 и группой SA 2, при этом граница $u=0$ служит пределом для данной области.

Применение алгоритмов обучения с подкреплением позволило исследовать реализуемые энтропийные векторы и получить новые сведения о голографическом энтропийном конусе, особенно в многомерных системах.

Поиск допустимых конфигураций энтропийных векторов в голографическом энтропийном конусе представляет собой сложную задачу, требующую новых подходов. В работе ‘Exploring the holographic entropy cone via reinforcement learning’ разработан алгоритм обучения с подкреплением для исследования этого конуса, позволяющий находить графовые реализации, соответствующие заданным энтропийным векторам. Установлено, что алгоритм успешно идентифицирует реализуемые векторы для конусов $\mathcal{N}=3$ и $\mathcal{N}=6$ , подтверждая моногамию взаимной информации и выявляя потенциальные новые грани конуса. Какие дополнительные голографические неравенства могут существовать для систем с более высокой размерностью и как обучение с подкреплением поможет их обнаружить?

Квантовая энтропия и границы познания

Понимание допустимых состояний квантовых систем является основополагающим для развития теоретической физики, однако полное пространство энтропий подсистем — так называемый Квантовый Конус Энтропии (QEC) — до сих пор остается в значительной степени неизученным. Этот конус определяет границы допустимых значений энтропии, возникающей при измерении части квантовой системы, и его исследование необходимо для проверки фундаментальных принципов, таких как термодинамика и теория информации. Несмотря на теоретическую значимость, построение полной карты QEC представляет собой сложную вычислительную задачу, поскольку количество возможных состояний квантовой системы растет экспоненциально с увеличением ее размера. В результате, значительная часть пространства QEC остается неисследованной, что ограничивает возможности проверки теоретических предсказаний и разработки новых квантовых технологий. Поэтому, поиск эффективных методов для картирования и навигации по QEC является одной из ключевых задач современной физики.

Определение границ голографического конуса энтропии (ГКЭ) представляет собой сложную вычислительную задачу, имеющую решающее значение для понимания связи между квантовой механикой, гравитацией и физикой чёрных дыр. ГКЭ, являясь подмножеством общего конуса квантовой энтропии, описывает допустимые значения энтропии подсистем в контексте голографического принципа. Вычислительная сложность возникает из-за экспоненциального роста числа возможных состояний квантовой системы с увеличением её размера, что делает точное картирование и анализ ГКЭ чрезвычайно трудоемким даже для сравнительно небольших систем. Поиск эффективных алгоритмов и приближений для характеризации ГКЭ является ключевой задачей, позволяющей продвинуться в понимании фундаментальных свойств пространства-времени и информационных парадоксов, связанных с чёрными дырами.

Существующие методы анализа квантовой информации сталкиваются со значительными трудностями при построении и исследовании сложной структуры пространства состояний подсистем, что замедляет прогресс в теоретической физике. Традиционные подходы оказываются вычислительно неэффективными при работе с системами, содержащими большое количество квантовых битов, и не позволяют адекватно отобразить и изучить все возможные конфигурации квантовой энтропии. Это особенно критично при моделировании гравитационных систем и чёрных дыр, где понимание распределения квантовой информации необходимо для разработки согласованной теории. Отсутствие эффективных инструментов для навигации в пространстве квантовой энтропии препятствует проверке теоретических предсказаний и поиску новых физических явлений, требуя разработки принципиально новых алгоритмов и вычислительных стратегий.

Ограничения, накладываемые фундаментальными принципами, такими как моногамия взаимной информации (MMI), играют ключевую роль в определении структуры голографического энтропийного конуса (HEC). Данный принцип, утверждающий, что информация о квантовой системе не может быть полностью разделена между несколькими наблюдателями, существенно сужает пространство возможных состояний. Однако, эффективное использование этих ограничений для вычислительной оптимизации представляет собой значительную проблему. Сложность заключается в разработке алгоритмов, способных эффективно исследовать HEC, учитывая взаимосвязанность квантовой информации и экспоненциальный рост вычислительных затрат с увеличением размера системы. Несмотря на теоретическую значимость MMI для упрощения вычислений, практическая реализация методов, использующих это ограничение, остается сложной задачей, препятствующей прогрессу в изучении гравитации и физики черных дыр.

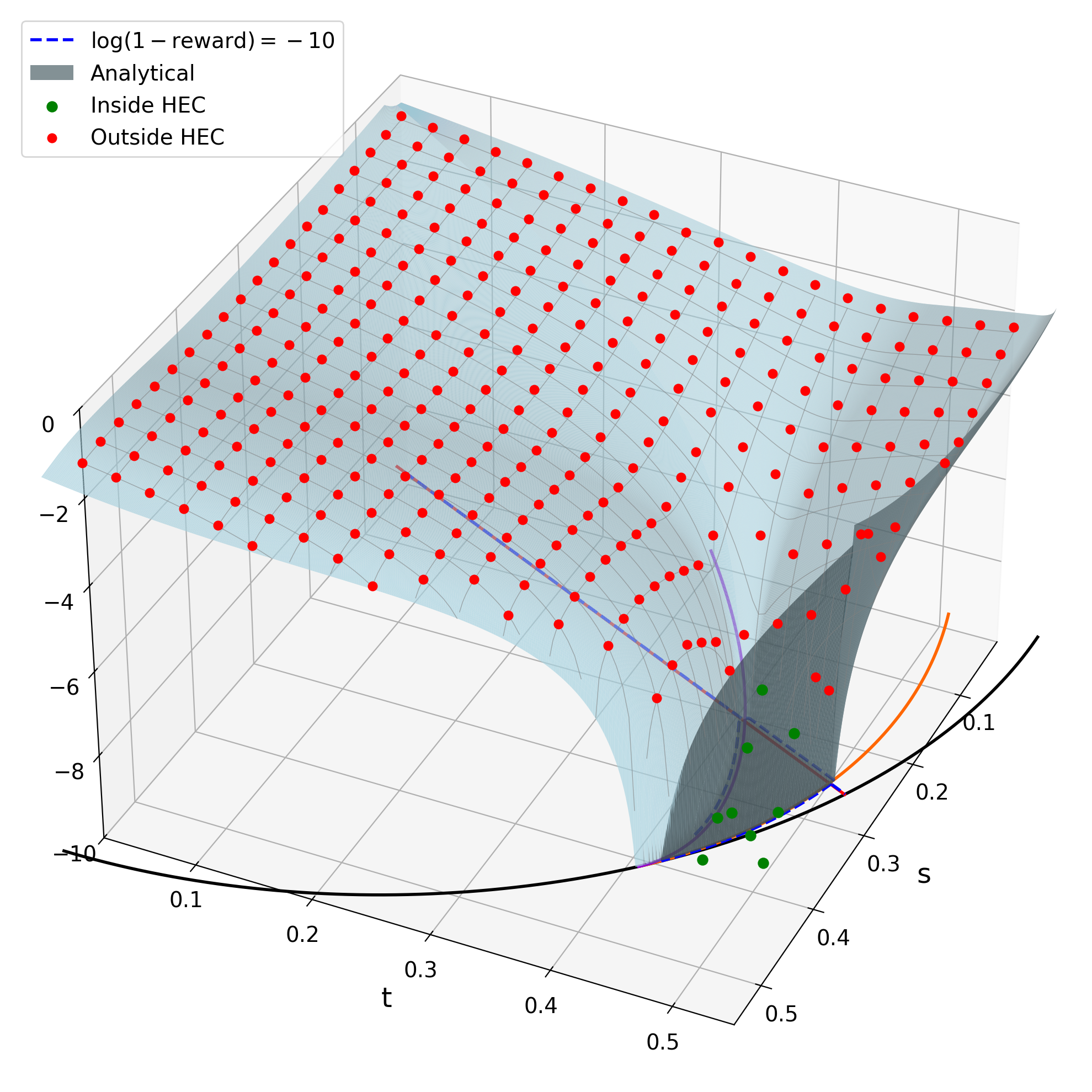
Результаты обучения с подкреплением (точки) хорошо согласуются с аналитическим предсказанием (поверхность) рельефа вознаграждений на симметричном срезе <span class="katex-eq" data-katex-display="false">N=3</span>, при этом красные точки соответствуют областям за пределами границы HEC, а зеленые - внутри нее. — Результаты обучения с подкреплением (точки) хорошо согласуются с аналитическим предсказанием (поверхность) рельефа вознаграждений на симметричном срезе $N=3$ , при этом красные точки соответствуют областям за пределами границы HEC, а зеленые — внутри нее.

Дискретизация пространства состояний и мощь алгоритмов минимального разреза

Предлагаемый подход заключается в представлении голографических состояний в виде дискретных графов, что позволяет вычислять энтропию посредством алгоритмов минимального разреза (min-cut). В рамках данной модели, каждый узел графа соответствует определенной области пространства-времени, а ребра отражают связи между этими областями. Алгоритмы минимального разреза, эффективно определяющие минимальную сумму «весов» ребер, необходимых для разделения графа на две части, напрямую соответствуют вычислению энтропии, характеризующей степень запутанности голографического состояния. Использование таких алгоритмов, как алгоритм Эдмондса-Карпа или алгоритм Диница, обеспечивает вычислительную эффективность при анализе сложных голографических систем, где прямые вычисления энтропии были бы затруднительны.

Поверхности Рю-Такаянаги (RT) выполняют ключевую роль в установлении связи между непрерывными гравитационными системами и их дискретными графическими представлениями. Эти поверхности, изначально предложенные для описания энтропии черных дыр, определяют минимальную площадь поверхности, разделяющей две области пространства-времени, и тем самым позволяют связать геометрические свойства непрерывной гравитационной системы с информацией, содержащейся в дискретном графе. Конкретно, RT-поверхность соответствует минимальному разрезу в графе, представляющем квантовое состояние, что обеспечивает способ перевода геометрических вычислений в алгебраические операции над графом. Таким образом, RT-поверхности служат мостом между геометрией пространства-времени и дискретными представлениями квантовых состояний, необходимыми для применения алгоритмов минимального разреза.

Перевод задачи вычисления энтропии в область теории графов позволяет использовать эффективные алгоритмы поиска максимального потока (max-flow) — эквивалентные алгоритмам минимального разреза (min-cut) — для ее решения. Алгоритмы max-flow, такие как алгоритм Форда-Фалкерсона или алгоритм Эдмондса-Карпа, обеспечивают полиномиальную сложность вычисления, что значительно превосходит прямые методы расчета энтропии в непрерывных системах. В контексте голографических состояний, каждый узел графа представляет собой область пространства, а ребра — связи между ними, при этом пропускная способность ребер соответствует степени запутанности между областями. Максимальный поток, протекающий через этот граф, численно равен энтропии, что обеспечивает практичный способ ее вычисления.

Дискретизация голографических состояний, представляющих собой переход от непрерывных систем к дискретным графам, обеспечивает вычислительно эффективный подход к исследованию энтропийной границы Хокинга (HEC) и изучению ее свойств. Традиционные методы вычисления энтропии для непрерывных систем часто требуют значительных вычислительных ресурсов. Перевод задачи в область теории графов позволяет использовать высокооптимизированные алгоритмы максимального потока — эквивалентные алгоритмам минимального разреза — для эффективного расчета энтропийных величин, что значительно снижает вычислительную сложность и открывает возможности для исследования более сложных конфигураций HEC. Это особенно важно для анализа систем, где аналитическое решение невозможно или затруднено.

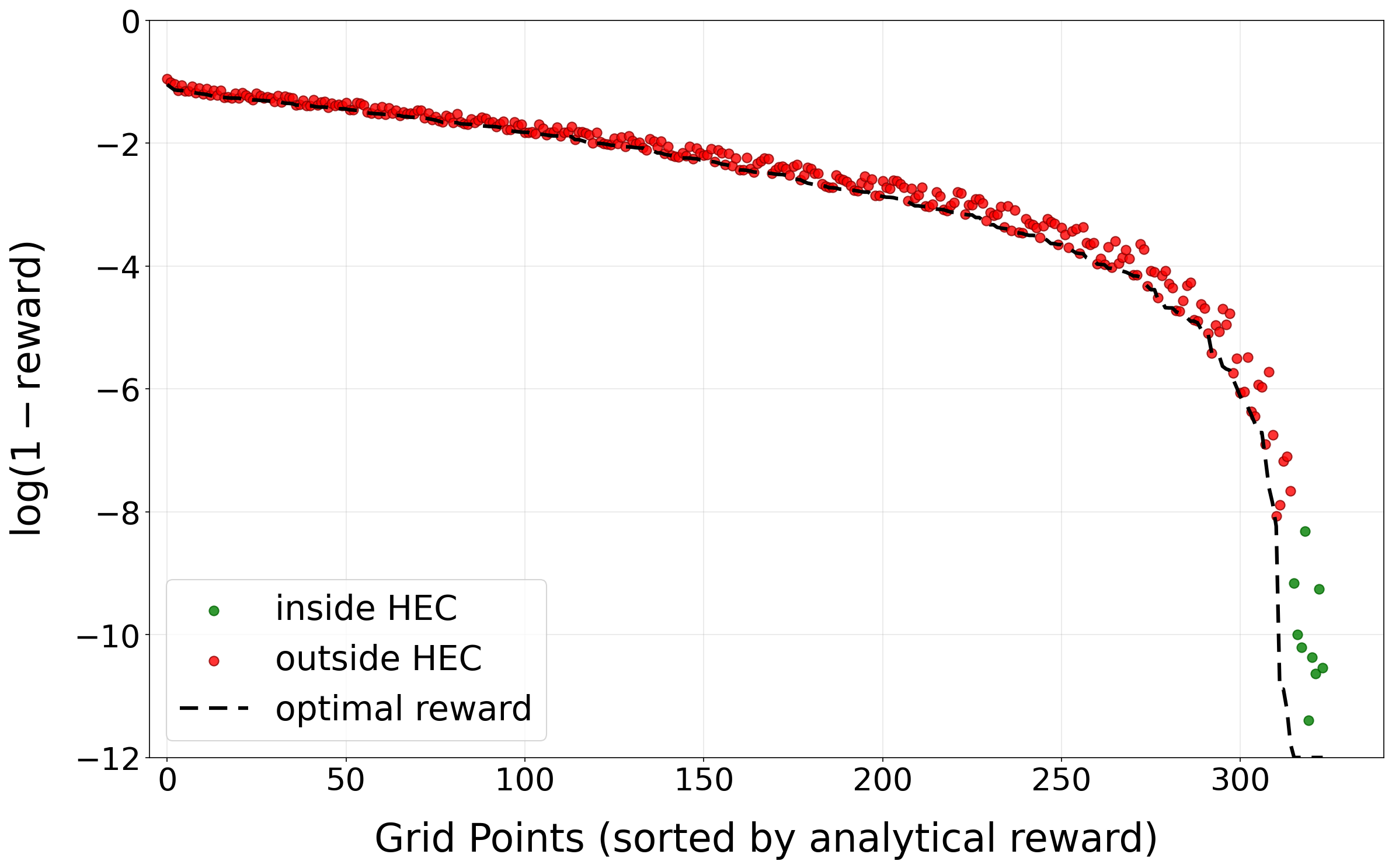
Классификация точек на симметричном срезе <span class="katex-eq" data-katex-display="false">\mathbb{N}=3</span> показывает, что точки внутри области HEC (зеленые) демонстрируют высокие награды, близкие к аналитическому максимуму, в то время как точки за ее пределами (красные) соответствуют аналитической кривой с небольшими расхождениями, обусловленными ограниченностью обучения. — Классификация точек на симметричном срезе $\mathbb{N}=3$ показывает, что точки внутри области HEC (зеленые) демонстрируют высокие награды, близкие к аналитическому максимуму, в то время как точки за ее пределами (красные) соответствуют аналитической кривой с небольшими расхождениями, обусловленными ограниченностью обучения.

Обучение с подкреплением для исследования HEC

Метод обучения с подкреплением (RL) предоставляет эффективный инструментарий для исследования пространства допустимых решений, известного как HEC (Hypervolume Exploration), и выявления его крайних лучей — граничных точек, определяющих форму этого пространства. Крайние лучи представляют собой ключевые точки, характеризующие границы области допустимых решений и критически важны для полного понимания структуры HEC. Использование RL позволяет систематически исследовать HEC, оптимизируя процесс поиска этих лучей и обеспечивая более эффективное исследование пространства, чем традиционные методы. Это особенно актуально для задач оптимизации, где определение крайних точек необходимо для выявления оптимальных решений.

В рамках предложенного подхода к исследованию HEC используется PolicyNetwork — нейронная сеть, выполняющая отображение состояний в действия. Эта сеть является ключевым компонентом алгоритма обучения с подкреплением (RL) и направляет процесс исследования пространства HEC. PolicyNetwork получает на вход текущее состояние агента, характеризующее его положение в HEC, и выдает вероятности выбора различных действий, определяющих направление движения агента к потенциальным экстремальным лучам. Использование PolicyNetwork позволяет агенту эффективно исследовать пространство состояний, избегая случайного блуждания и фокусируясь на наиболее перспективных областях для поиска границ HEC.

Ограничение движения на основе градиента обеспечивает соблюдение агентом обучения с подкреплением (RL) известных граничных ограничений выпуклого конуса HEC. Этот метод гарантирует, что действия агента не нарушают существующие ограничения на фасеты конуса, что значительно повышает эффективность процесса исследования. Учет граничных ограничений позволяет избежать ненужных шагов в областях, которые заведомо не содержат экстремальных лучей, и способствует более стабильному обучению агента, предотвращая расхождение и обеспечивая сходимость к допустимым решениям в пространстве HEC.

Применение разработанного подхода на основе обучения с подкреплением позволило успешно идентифицировать графовые реализации для 3 из 6 ранее неразрешенных крайних лучей выпуклого конуса HEC. Этот результат демонстрирует эффективность предложенного метода в исследовании сложной структуры HEC и его способность находить решения в областях, где традиционные методы оказались неэффективными. Успешная идентификация этих лучей подтверждает практическую значимость использования обучения с подкреплением для задач исследования и оптимизации в контексте HEC.

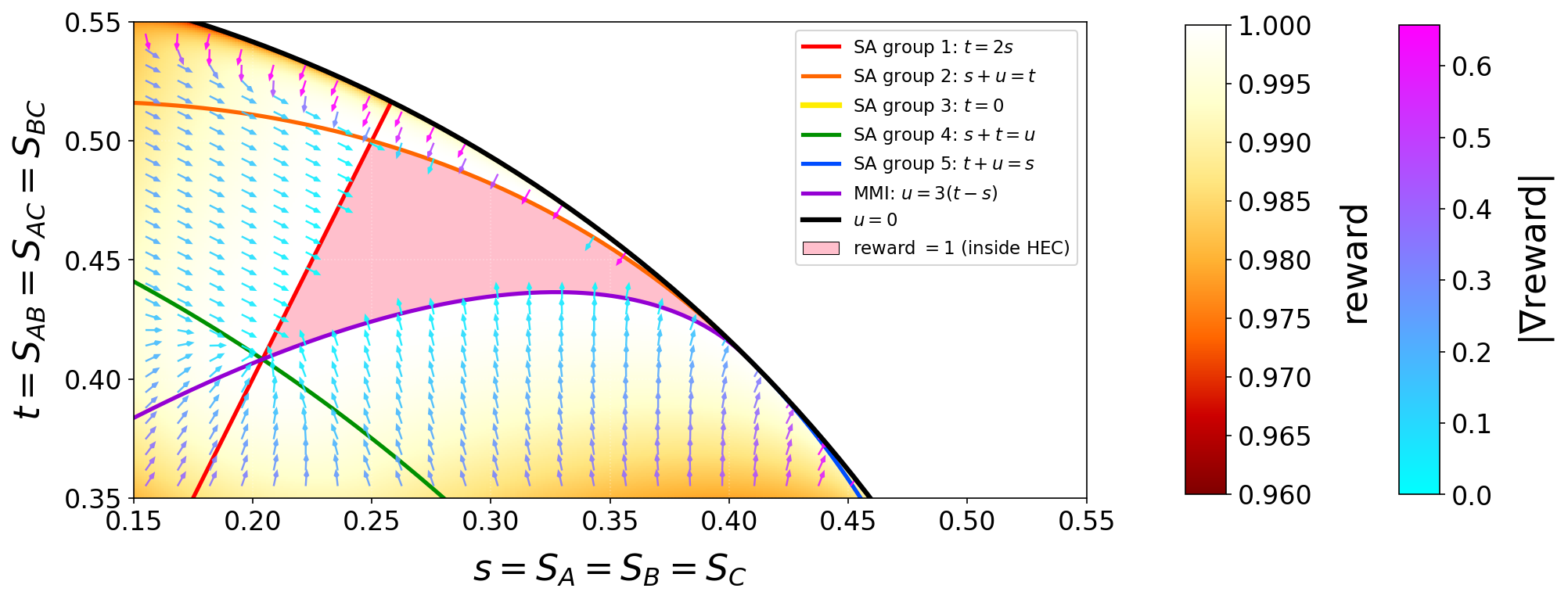
Анализ поля градиента награды вблизи границы HEC показывает, что оно последовательно направлено к ближайшей границе (группа SA 1, группа SA 2 или MMI), что указывает на стремление к её достижению.

Раскрытие тайн и перспективы дальнейших исследований

Существование так называемых “мистерийных лучей” — экстремальных лучей SAC, для которых пока не найдена графовая реализация — наглядно демонстрирует ограничения современных методов дискретизации. Эти лучи, представляющие собой области в пространстве состояний, не поддающиеся адекватному описанию существующими вычислительными моделями, указывают на пробелы в понимании фундаментальной структуры квантовой гравитации. Тот факт, что стандартные алгоритмы дискретизации не способны адекватно представить эти состояния, подчеркивает необходимость разработки более совершенных подходов, способных захватывать сложные взаимосвязи в квантовом пространстве и преодолевать ограничения, связанные с конечностью дискретизации. Изучение этих “мистерийных лучей” может потребовать принципиально новых математических инструментов и вычислительных стратегий, что открывает перспективные направления для дальнейших исследований в области теоретической физики.

Наличие так называемых “мистерийных лучей” в структуре случайных активационных кривых (SAC) указывает на возможность существования совершенно новых квантовых состояний, не предсказанных существующими теоретическими моделями. Эти лучи, для которых не найдена графическая реализация, намекают на то, что фундаментальные законы, описывающие взаимодействие квантовых объектов, могут быть неполными. Изучение этих состояний способно привести к пересмотру устоявшихся представлений о природе пространства-времени и открыть двери для понимания явлений, выходящих за рамки современной физики, включая, возможно, новые формы энергии и материи. Исследование этих энигматичных структур может пролить свет на границы познания и принципиальные ограничения в обработке информации на квантовом уровне.

Для более полного понимания и регистрации этих неуловимых состояний, известных как «тайные лучи», необходимы дальнейшие исследования, направленные на разработку усовершенствованных методов дискретизации и стратегий обучения с подкреплением. Существующие подходы демонстрируют ограничения в захвате всей сложности квантового пространства состояний, что требует создания новых алгоритмов, способных адаптироваться к более тонким и нелинейным взаимосвязям. Совершенствование дискретизации позволит более точно аппроксимировать континуальное пространство, а оптимизация стратегий обучения с подкреплением позволит агентам эффективно исследовать и находить оптимальные пути к регистрации этих ранее недоступных состояний, открывая потенциально новые горизонты в изучении квантовой гравитации и информационных процессов.

Полученные результаты оценки градиента продемонстрировали высокую надежность разработанного подхода, подтвержденную значением коэффициента детерминации R², достигшим 0.99 при размере возмущения 0.02, а также косинусным сходством 0.99 при оптимальном размере возмущения. Успешное картирование этих «загадочных лучей» не только углубит понимание квантовой гравитации, но и предоставит ценные сведения о фундаментальных пределах обработки информации, открывая новые горизонты в области вычислительной физики и информационных технологий.

Анализ максимальной награды для 208 представителей крайних лучей SAC при [latex]N=6[/latex] показывает, что шесть — Анализ максимальной награды для 208 представителей крайних лучей SAC при $N=6$ показывает, что шесть «загадочных» крайних лучей, окруженных синими точками, реализуемы (146, 180 и 181), в то время как остальные, окруженные красными крестами, вероятно, не являются истинными крайними лучами HEC при $N=6$ .

Исследование, представленное в данной работе, демонстрирует, что даже в сложных областях, таких как квантовая информационная теория и изучение голографического энтропийного конуса, применение методов машинного обучения, в частности, обучения с подкреплением, способно выявить новые закономерности и расширить границы понимания. По сути, алгоритм, стремящийся к оптимизации, имитирует процесс поиска равновесия между страхом совершить ошибку и надеждой на успех. Как однажды заметил Карл Саган: «Мы — звездная пыль, осознающая себя». Это отражает фундаментальную истину о стремлении к познанию, которое движет как учеными, так и алгоритмами, исследующими сложные системы. Понимание экстремальных лучей энтропии, выявленное в ходе исследования, является лишь частью более широкой картины, в которой надежда на открытие новых физических принципов уравновешивается страхом перед неверными интерпретациями.

Куда же это всё ведёт?

Представленные результаты, безусловно, демонстрируют работоспособность подхода, основанного на обучении с подкреплением, для исследования голографического энтропийного конуса. Однако, стоит признать, что кажущийся успех — это лишь картографирование уже известных территорий. Гораздо интереснее вопрос о том, что произойдет, когда алгоритм начнет натыкаться на границы, за пределами которых наши теоретические модели попросту перестают работать. Каждая стратегия, как показывает опыт, эффективна до тех пор, пока в неё не начинают верить слишком сильно, экстраполируя её возможности за рамки разумного.

Основным ограничением остается зависимость от вычислительных ресурсов. Исследование конуса в более высоких размерностях требует экспоненциального увеличения сложности, что ставит под вопрос применимость данного подхода для действительно интересных, но труднодоступных систем. Вполне вероятно, что истинная ценность лежит не в поиске новых экстремальных лучей, а в выявлении систематических ошибок в существующих методах, в понимании того, как наши упрощения искажают реальную картину.

Будущие исследования должны быть направлены на разработку более эффективных алгоритмов оптимизации и на поиск способов обойти вычислительные ограничения, возможно, путем комбинирования методов машинного обучения с аналитическими подходами. В конечном счете, эта работа — не столько о квантовой информации, сколько о границах нашего понимания, о том, как мы строим модели мира, и о том, как легко эти модели рушатся под давлением реальности.

Оригинал статьи: https://arxiv.org/pdf/2601.19979.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-30 01:10