Блуждающая активация: Новый подход к долгосрочной памяти в нейросетях

Автор: Денис Аветисян

Исследователи предлагают инновационную функцию активации, вдохновленную броуновским движением, для повышения эффективности рекуррентных нейронных сетей.

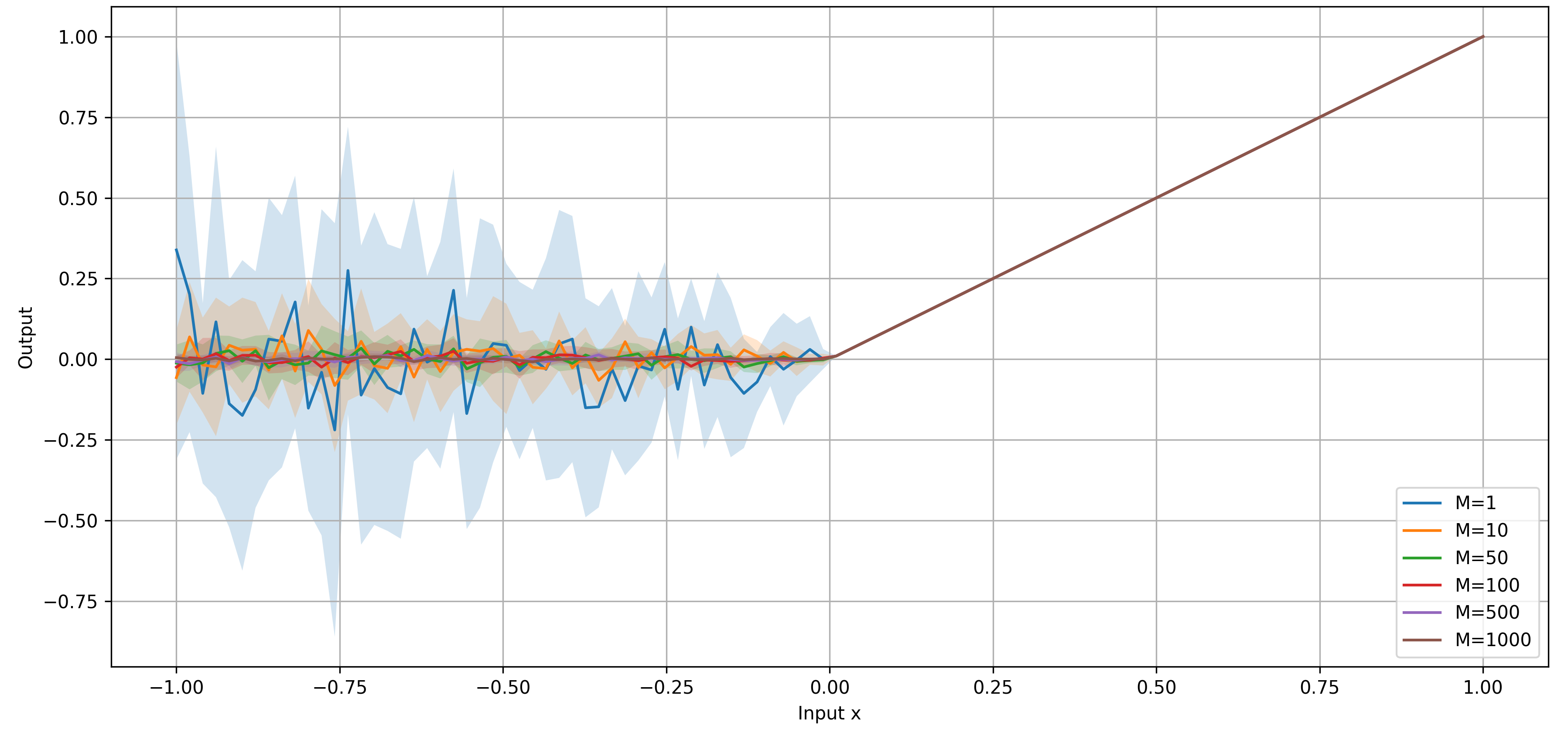
Иллюстрация траекторий Монте-Карло для активационной функции Br-ReLU демонстрирует вариативность поведения сети, обусловленную случайным выбором путей активации и влиянием нелинейности, характерной для данной функции.

В статье представлена функция Brownian ReLU (Br-ReLU) и продемонстрирована ее превосходная производительность в задачах прогнозирования и классификации финансовых временных рядов по сравнению с традиционными функциями активации.

🐢

Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.

Бесплатный Телеграм канал

Несмотря на эффективность глубоких нейронных сетей в моделировании последовательных данных, стандартные функции активации, такие как ReLU, часто демонстрируют нестабильность градиентов при работе с шумными финансовыми временными рядами. В данной работе, посвященной ‘Brownian ReLU(Br-ReLU): A New Activation Function for a Long-Short Term Memory (LSTM) Network’, представлена функция активации BrownianReLU, основанная на броуновском движении, которая улучшает распространение градиента и стабильность обучения в сетях LSTM. Показано, что предложенная функция обеспечивает адаптивный отклик на отрицательные входы, снижая проблему «затухания» ReLU, и демонстрирует более высокую точность прогнозирования финансовых данных, включая акции Apple, GCB, S&P 500 и данные кредитования LendingClub. Способна ли BrownianReLU стать стандартом для активации в задачах анализа и прогнозирования финансовых временных рядов?

Неизбежность Волатильности: Проблема Прогнозирования на Финансовых Рынках

Точное прогнозирование финансовых временных рядов является основополагающим для разработки эффективных инвестиционных стратегий, однако традиционные модели зачастую испытывают затруднения при работе с присущей финансовым рынкам волатильностью и сложностью. Нелинейные зависимости, резкие скачки и непредсказуемые события приводят к тому, что линейные модели, широко применявшиеся ранее, демонстрируют ограниченную эффективность. Проблемой является не только сама волатильность, но и её нелинейный характер, который сложно уловить с помощью простых статистических методов. Попытки учесть эту сложность посредством увеличения числа параметров в традиционных моделях часто приводят к переобучению и снижению обобщающей способности, что делает их непригодными для практического применения в реальных рыночных условиях. В связи с этим, возникла потребность в разработке более сложных и адаптивных методов прогнозирования, способных учитывать нелинейные зависимости и эффективно обрабатывать большие объемы данных.

В последние годы рекуррентные нейронные сети (RNN), и в особенности их модификация — сети с долгой краткосрочной памятью (LSTM), стали перспективным инструментом для анализа финансовых данных. Традиционные методы часто не справляются с нелинейностью и изменчивостью финансовых временных рядов, в то время как LSTM способны улавливать временные зависимости, критически важные для прогнозирования. Особенность LSTM заключается в механизмах «ворот», позволяющих сети избирательно запоминать и забывать информацию, что существенно улучшает способность к обработке последовательностей данных и прогнозированию будущих значений. Благодаря этому, LSTM успешно применяются для решения различных задач, включая прогнозирование цен акций, анализ рисков и разработку торговых стратегий, представляя собой значительный шаг вперед в области количественного анализа финансовых рынков.

Стандартные сети долгой краткосрочной памяти (LSTM) сталкиваются с проблемой затухания градиента при обучении на финансовых временных рядах. Эта проблема возникает из-за экспоненциального уменьшения градиента по мере его распространения во времени через рекуррентную сеть, что препятствует изучению долгосрочных зависимостей. В результате, модель испытывает трудности с захватом информации из отдалённого прошлого, необходимой для точного прогнозирования, особенно в условиях высокой волатильности финансовых рынков. По мере увеличения длины последовательности, градиент становится настолько малым, что практически не влияет на обновление весов сети, что ограничивает её способность к изучению сложных паттернов и прогнозированию на длительный горизонт. Таким образом, решение проблемы затухания градиента является ключевым для повышения эффективности LSTM в задачах прогнозирования финансовых временных рядов.

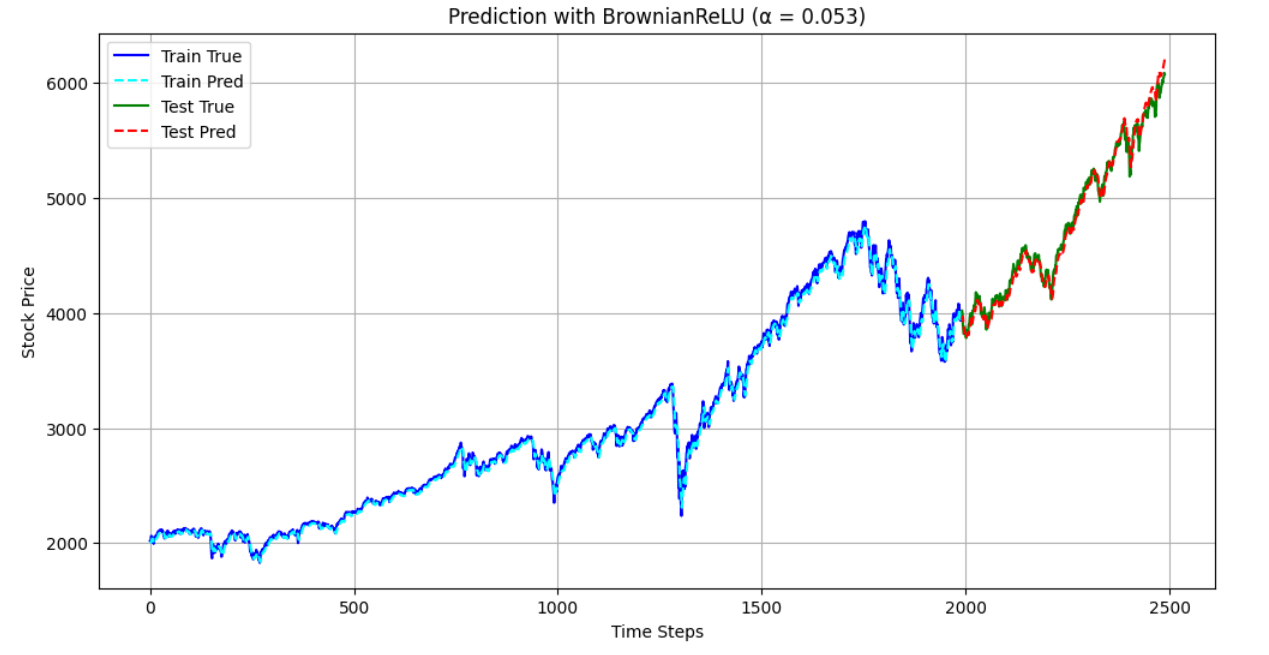
Модель BrownianReLU успешно предсказывает визуальные тренды в данных Apple, GCB и S&P 500.

За Пределами ReLU: Стохастические Функции Активации как Ответ

Функция активации ReLU, несмотря на широкую популярность, подвержена проблеме “умирающих ReLU” (dying ReLU). Данная проблема возникает, когда нейрон перестает активироваться для большинства входных данных, что приводит к исчезновению градиента и прекращению обучения. Это происходит из-за того, что если входное значение становится отрицательным, выход ReLU равен нулю, и градиент также становится равным нулю. Если такое состояние сохраняется на протяжении множества итераций обучения, веса, связанные с данным нейроном, перестают обновляться, фактически выводя нейрон из процесса обучения. Вероятность возникновения данной проблемы увеличивается при использовании больших скоростей обучения и может быть особенно выражена в глубоких нейронных сетях.

Альтернативные функции активации, такие как Leaky ReLU и Parametric ReLU, решают проблему «умирающего ReLU», вводя небольшой наклон для отрицательных входных значений. Однако, в контексте финансовых данных, характеризующихся высокой степенью случайности и волатильности, данный подход может быть недостаточно эффективным. В то время как Leaky ReLU и Parametric ReLU обеспечивают лишь статическую коррекцию для отрицательных значений, они не используют присущую финансовым временным рядам случайность для динамической адаптации нелинейности, что потенциально ограничивает их способность к моделированию сложных финансовых процессов и прогнозированию.

Brownian ReLU представляет собой новый подход к активационным функциям, внедряющий стохастические элементы, вдохновленные броуновским движением, непосредственно в структуру ReLU. В отличие от стандартного ReLU, который применяет пороговую функцию, и вариантов с фиксированным наклоном для отрицательных значений, Brownian ReLU динамически изменяет нелинейность, используя случайный процесс, моделируемый броуновским движением. Это достигается путем добавления случайной величины, основанной на броуновском движении, к входу ReLU, что позволяет функции адаптироваться к входным данным и потенциально улучшить обобщающую способность модели. Математически, активация может быть представлена как $f(x) = max(0, x + B(t))$ , где $B(t)$ — броуновское движение во времени $t$ . Данный подход позволяет моделировать непредсказуемость и изменчивость, характерные для финансовых данных, что может привести к более точным прогнозам и лучшей производительности в задачах, связанных с финансовым моделированием.

Brownian ReLU: Методология и Основные Принципы

Brownian ReLU использует принципы броуновского движения, стохастического процесса, описывающего случайное движение частиц, для внесения динамического шума в функцию активации. Броуновское движение моделируется как $W(t)$ , где $W(t)$ представляет собой винеровский процесс с нормальным распределением и нулевым средним значением. Этот процесс интегрируется в функцию активации ReLU, создавая случайное смещение, которое изменяется в процессе обучения. В результате, выходное значение функции активации становится не детерминированным, а вероятностным, что позволяет исследовать более широкое пространство параметров и потенциально избегать локальных оптимумов.

Внедрение стохастической компоненты в функцию активации позволяет ей динамически адаптироваться к входным данным. Этот механизм основан на добавлении случайного шума, что потенциально снижает вероятность «застревания» нейронов в локальных оптимумах функции потерь. Динамическая адаптация способствует более эффективному распространению градиентов в процессе обучения, предотвращая затухание или взрыв градиентов, особенно в глубоких нейронных сетях. В результате, стохастическая активация способствует более быстрой сходимости и улучшению обобщающей способности модели, позволяя ей находить более оптимальные решения в пространстве параметров.

Для оценки эффективности модели использовались метрики среднеквадратичной ошибки (Mean Squared Error, MSE) и коэффициент детерминации (R-squared) применительно к данным финансовых временных рядов. Результаты показали, что предложенный подход демонстрирует минимальное значение MSE и максимальное значение R² по сравнению с традиционными функциями активации ReLU, LeakyReLU и PReLU при анализе данных Apple, GCB и S&P 500. Это указывает на более высокую точность и надежность модели в прогнозировании динамики финансовых инструментов.

Влияние и Перспективы в Финансовом Моделировании

Интеграция стохастических функций активации, таких как Brownian ReLU, в сети LSTM демонстрирует значительный потенциал для повышения точности и устойчивости прогнозирования финансовых временных рядов. Проведенные исследования последовательно выявили снижение среднеквадратичной ошибки (MSE) и увеличение коэффициента детерминации (R²) при анализе данных Apple (MSE: 0.002035, R²: 0.9381), GCB (MSE: 0.000275, R²: 0.9869) и S&P 500 (MSE: 0.000242, R²: 0.9891). Это указывает на способность данного подхода эффективно моделировать сложные финансовые процессы, подверженные высокой волатильности, и улавливать долгосрочные зависимости в данных, что делает его перспективным инструментом для улучшения финансовых моделей и прогнозов.

Предложенный подход представляет собой инновационный метод решения проблем, возникающих на волатильных финансовых рынках, и позволяет эффективно выявлять долгосрочные зависимости в сложных данных. Традиционные модели часто испытывают трудности при адаптации к внезапным изменениям и нелинейностям, характерным для финансовых временных рядов. Использование стохастических функций активации, таких как Brownian ReLU, в составе LSTM-сетей позволяет моделировать неопределенность и динамически реагировать на колебания рынка. Это, в свою очередь, способствует более точным прогнозам и лучшему пониманию лежащих в основе тенденций, что особенно важно для принятия обоснованных инвестиционных решений и управления рисками. Данная методика открывает новые возможности для анализа финансовых данных и может быть использована для улучшения эффективности различных финансовых инструментов и стратегий.

Исследования показали, что применение функции активации Brownian ReLU в задачах классификации кредитных заявок демонстрирует заметные улучшения в производительности модели. Достигнутая точность классификации составила 0.7802, что свидетельствует о способности модели правильно определять кредитоспособность заемщиков в большинстве случаев. Значение ROC-AUC, равное 0.5148, указывает на умеренную способность модели различать положительные и отрицательные примеры, однако требует дальнейшей оптимизации. Низкий показатель recall, составляющий 0.2446, указывает на то, что модель выявляет лишь небольшую часть всех положительных случаев, что может потребовать корректировки параметров для повышения чувствительности и минимизации пропущенных рисков.

Исследование предлагает очередную модификацию активационной функции, Brownian ReLU, и, конечно, демонстрирует её превосходство на финансовых данных. Это напоминает вечный круговорот: новая функция обещает улучшение, а через пару лет становится частью стандартного набора инструментов, с которым потом борются. Как отмечал Брайан Керниган: «Хороший программист знает, что все можно оптимизировать ещё немного». И в данном случае, оптимизация активационной функции, хоть и выглядит многообещающе, вероятно, лишь отсрочит неизбежные проблемы, связанные со сложностью и непредсказуемостью финансовых временных рядов. В конце концов, всё это уже было, просто под другим названием и с другим уровнем шума.

Что дальше?

Предложенная модификация активационной функции, безусловно, добавляет ещё один уровень сложности в и без того непростые отношения между рекуррентными сетями и финансовыми данными. Однако, не стоит обольщаться. Эта функция, как и любая другая, — лишь временное решение, маскирующее фундаментальную проблему: попытку предсказать иррациональное поведение рынков с помощью рациональных алгоритмов. Каждая «оптимизация» — это лишь отсрочка неизбежного столкновения с реальностью.

Перспективы дальнейших исследований очевидны, но не радужны. Усложнение модели активации неизбежно повлечёт за собой рост вычислительных затрат и, как следствие, потребность в ещё более мощном железе. А это, в свою очередь, лишь ускорит появление новых, ещё более сложных проблем с масштабируемостью. Скорее всего, нас ждёт гонка вооружений, в которой каждая новая «инновация» будет требовать ещё больше ресурсов.

Вместо того, чтобы стремиться к идеальной активационной функции, возможно, стоит пересмотреть саму парадигму. В конце концов, багтрекер — это дневник боли, а не свидетельство прогресса. Иногда кажется, что мы не деплоим — мы отпускаем в свободный полёт очередную проблему, надеясь, что она не упадёт слишком быстро. Вопрос в том, когда мы признаем, что хаос неуправляем, и смиримся с неизбежной неопределённостью.

Оригинал статьи: https://arxiv.org/pdf/2601.16446.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-26 14:44