Автор: Денис Аветисян
Исследователи предлагают быстрый и точный метод моделирования движения звезд в галактиках, основанный на машинном обучении.
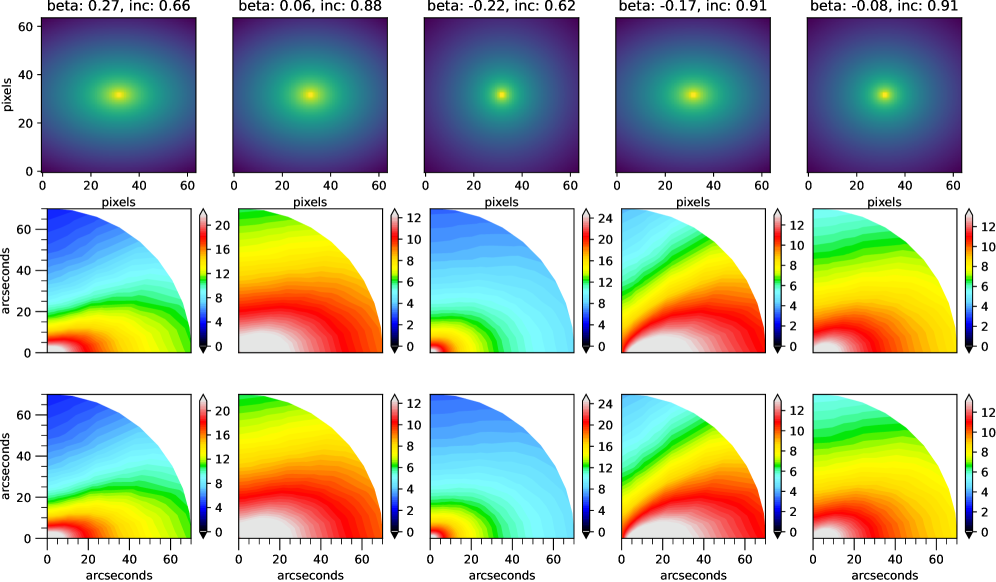
В статье представлен подход с использованием нейронных сетей для динамического моделирования галактик, сопоставимый по точности с традиционными методами, но значительно превосходящий их по скорости.
Несмотря на значительный прогресс в изучении эволюции галактик на основе кинематических данных, традиционные методы динамического моделирования часто опираются на упрощающие предположения, не всегда применимые к реальным объектам. В работе «Динамическое моделирование галактической кинематики с использованием нейронных сетей» представлен новый подход, основанный на обучении нейронных сетей на данных, полученных с помощью метода Jeans Anisotropic Modelling (JAM). Показано, что разработанная методика позволяет достичь сопоставимой с традиционными моделями точности, при значительном увеличении скорости расчетов. Какие перспективы открываются для применения машинного обучения в решении задач галактической динамики и моделировании более сложных галактических систем?
Свет и Тьма: Вызовы Динамического Моделирования Галактик
Традиционные методы динамического моделирования галактик, направленные на определение их ключевых параметров, исторически опирались на ряд упрощающих предположений и требовали значительных вычислительных ресурсов. Например, метод многокомпонентного разложения (MGE) — широко используемый подход для реконструкции массового распределения — предполагает, что галактика состоит из набора простых, математически описанных компонентов. Хотя MGE и позволяет получить разумные оценки параметров, он чувствителен к начальным условиям и требует тщательной калибровки. Кроме того, сложность галактик и неоднозначность в интерпретации наблюдаемых данных часто приводят к неточностям и погрешностям в полученных моделях. Эта вычислительная дороговизна и зависимость от предположений стимулируют поиск альтернативных, более эффективных и надежных подходов к определению параметров галактик, способных более точно отражать их истинную динамику и структуру.
Восстановление распределения массы из наблюдаемого света является ключевой задачей в изучении галактик, однако этот процесс сопряжен с существенными трудностями. Наблюдаемые световые характеристики, такие как яркость и спектр, не однозначно определяют лежащую в основе массу. Различные конфигурации массы могут приводить к схожим световым профилям, что порождает так называемые вырождения. Кроме того, даже незначительные погрешности в измерениях света или неточности в моделях звездного населения могут приводить к значительным ошибкам в оценке массы. Это требует разработки сложных методов моделирования и анализа данных, а также тщательной оценки неопределенностей, чтобы получить достоверное представление о массе и структуре галактик. Точное определение распределения массы необходимо для понимания динамики галактик, их формирования и эволюции, а также для проверки космологических моделей.
Традиционные методы динамического моделирования галактик часто сталкиваются с трудностями при эффективном исследовании многомерного пространства параметров, необходимых для точного описания их структуры и эволюции. Проблема заключается в том, что даже небольшие изменения в начальных предположениях могут приводить к существенно отличающимся результатам, что затрудняет определение наиболее вероятной модели. Кроме того, оценка неопределенностей, связанных с полученными параметрами, требует значительных вычислительных ресурсов и часто оказывается неполной. Это связано с тем, что пространство параметров обладает сложной структурой, включающей множество локальных минимумов и вырожденностей, что делает поиск глобального оптимума чрезвычайно сложной задачей. В результате, получаемые модели могут быть неточными, а оценка их надежности — недостаточной для проведения дальнейших исследований.
В связи со сложностями, возникающими при традиционном динамическом моделировании галактик, все большее внимание привлекают подходы, основанные на анализе данных. Вместо того, чтобы опираться на предположения и трудоемкие вычислительные методы, такие как разложение на компоненты МДЖ, предлагается непосредственно изучать связь между наблюдаемым светом галактики и ее внутренними динамическими параметрами. Этот подход позволяет построить модель, способную «обучаться» на большом объеме данных и выявлять закономерности, которые остаются незамеченными при использовании традиционных методов. В результате появляется возможность более эффективно исследовать пространство параметров и оценивать неопределенности в полученных динамических моделях, что открывает новые перспективы для понимания формирования и эволюции галактик.
Свет в Коде: Нейронная Сеть для Динамических Параметров
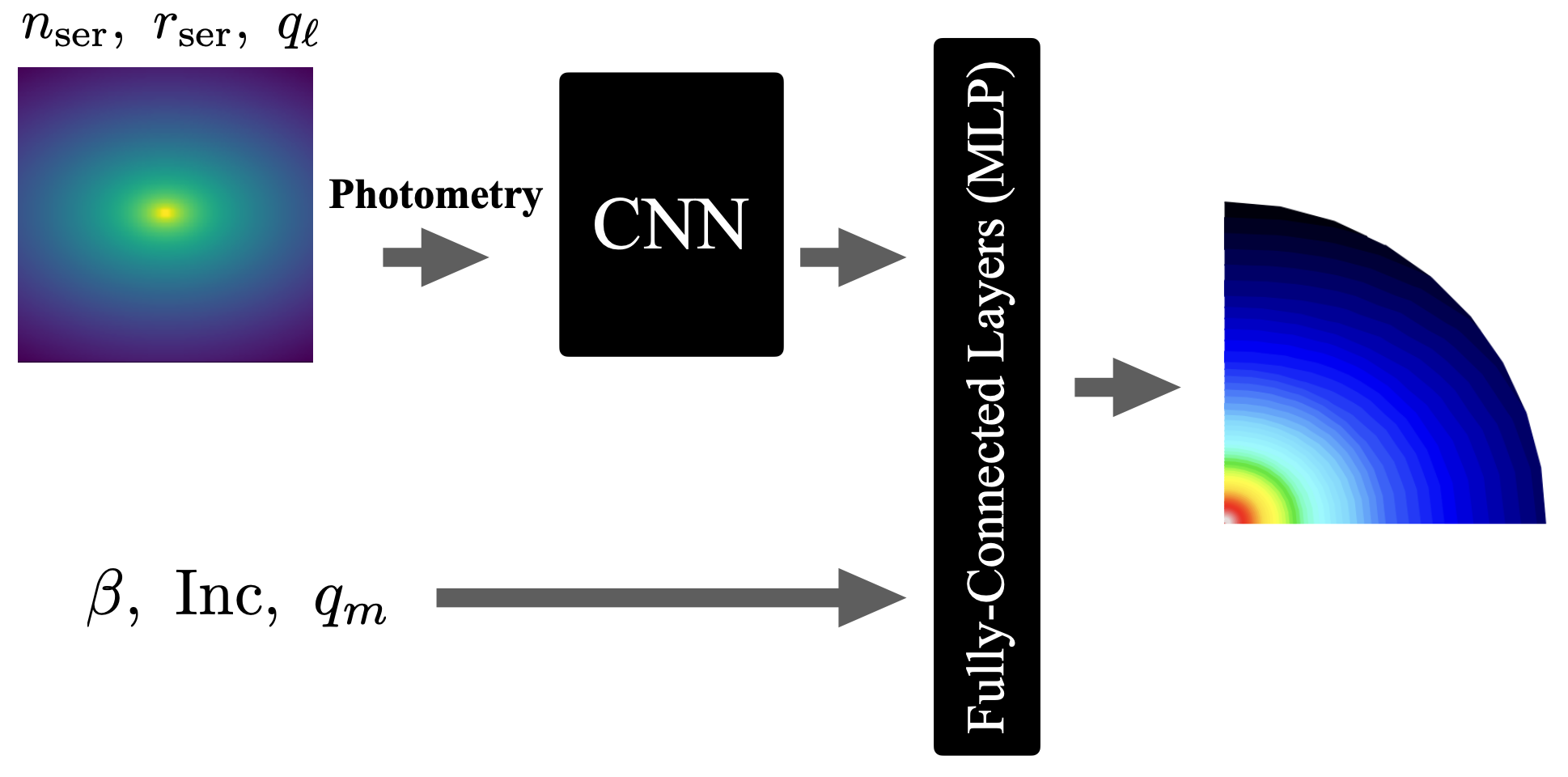
Для извлечения устойчивых признаков из данных, имитирующих фотометрию галактик, используется сверточная нейронная сеть (CNN). Входными данными для CNN являются изображения, представляющие распределение света галактики. Сверточные слои CNN автоматически обучаются выделять важные пространственные паттерны и характеристики, такие как яркость, форма и текстура. Эти признаки, полученные из анализа распределения света, служат основой для последующего анализа и реконструкции карт второго момента, а также предсказания динамических параметров галактики. Использование CNN обеспечивает устойчивость к шуму и вариациям в данных, что критически важно для точного анализа.
Извлеченные признаки из данных фотометрии поступают на вход многослойного персептрона (MLP) для восстановления карт второго момента и предсказания динамических параметров галактик. MLP используется для прямого сопоставления признаков с наблюдаемыми величинами, характеризующими движение звезд в галактике, такими как дисперсия скоростей и кинематическая асимметрия. Восстановленные карты второго момента предоставляют информацию о форме и ориентации звездного диска, а предсказанные динамические параметры позволяют оценить массу галактики и ее внутреннюю структуру без необходимости использования традиционных моделей, основанных на предположениях о распределении звезд и темной материи.
Многослойный персептрон использует функции активации LeakyReLU для введения нелинейности и повышения репрезентационной способности модели. В отличие от традиционных функций активации, таких как сигмоида или ReLU, LeakyReLU позволяет градиенту проходить даже при отрицательных входных значениях, что предотвращает проблему “затухающего градиента” и способствует более эффективному обучению. Математически, LeakyReLU определяется как f(x) = max(0, x) + \alpha min(0, x) , где α — небольшая константа (обычно 0.01). Внедрение этой нелинейности позволяет персептрону моделировать более сложные взаимосвязи между входными признаками и выходными динамическими параметрами, что критически важно для точного восстановления карт второго момента и предсказания динамических характеристик галактик.
Архитектура нейронной сети позволяет установить непосредственное, обучаемое соответствие между наблюдаемым распределением света галактики и ключевыми динамическими параметрами, такими как дисперсия скоростей и кинематические моменты. В отличие от традиционных методов, требующих предварительного построения моделей для описания формы и движения галактик, данная система извлекает информацию напрямую из данных фотометрии. Это устраняет необходимость в ручной настройке параметров моделей и снижает влияние систематических ошибок, связанных с упрощающими предположениями о внутренней структуре галактики. Обученная сеть эффективно “выучивает” связь между светом и динамикой, предоставляя возможность более точной и быстрой оценки динамических свойств галактик по данным наблюдений.
Калибровка Вселенной: Обучение и Оптимизация Модели
Многослойный персептрон обучается с использованием оптимизатора Adam и функции потерь среднеквадратичной ошибки (Mean Squared Error, MSE) для минимизации расхождения между предсказанными и истинными динамическими параметрами. Оптимизатор Adam автоматически адаптирует скорость обучения для каждого параметра, что способствует более быстрой и стабильной сходимости. Функция потерь MSE вычисляет среднюю квадратичную разницу между предсказанными значениями и целевыми значениями, предоставляя меру ошибки, которую алгоритм стремится минимизировать. Минимизация этой функции потерь приводит к обучению модели, способной точно предсказывать динамические параметры на основе входных данных.
Для повышения сходимости и стабильности процесса обучения модели используется алгоритм ReduceLROnPlateau. Данный алгоритм динамически регулирует скорость обучения (learning rate) в процессе тренировки. Если значение функции потерь на валидационной выборке перестает уменьшаться (достигает плато) в течение определенного числа эпох, скорость обучения автоматически уменьшается. Это позволяет модели более точно настроить параметры вблизи минимума функции потерь и избежать осцилляций, что способствует более быстрой сходимости и предотвращает переобучение. Параметры алгоритма, такие как число эпох без улучшений и коэффициент уменьшения скорости обучения, настраиваются эмпирически для достижения оптимальной производительности.
Эффективность модели напрямую зависит от значения параметра Beta, который используется в коде JAM для выборки физически правдоподобных решений уравнения Джинса. Параметр Beta служит ограничением при генерации решений, влияя на диапазон и стабильность полученных распределений скоростей и плотностей. Некорректный выбор значения Beta может привести к получению нефизических решений, либо к сужению пространства возможных решений, что снижает точность инференса динамических параметров. Экспериментально установлено, что оптимальное значение Beta варьируется в зависимости от конкретных характеристик исследуемой галактики и требует тщательной калибровки для достижения максимальной производительности.
Тщательный процесс обучения обеспечивает точное установление связи между наблюдаемым светом и динамическими параметрами исследуемой системы. Оптимизация с использованием алгоритма Adam и функции потерь среднеквадратичной ошибки (Mean Squared Error) минимизирует расхождения между предсказанными и истинными значениями динамических параметров. Дополнительно, применение ReduceLROnPlateau позволяет динамически регулировать скорость обучения при достижении плато в валидационной функции потерь, повышая стабильность и скорость сходимости модели. В результате, модель способна эффективно извлекать информацию о динамике системы на основе анализа световых данных.
Взгляд в Будущее: Валидация и Влияние Нового Подхода
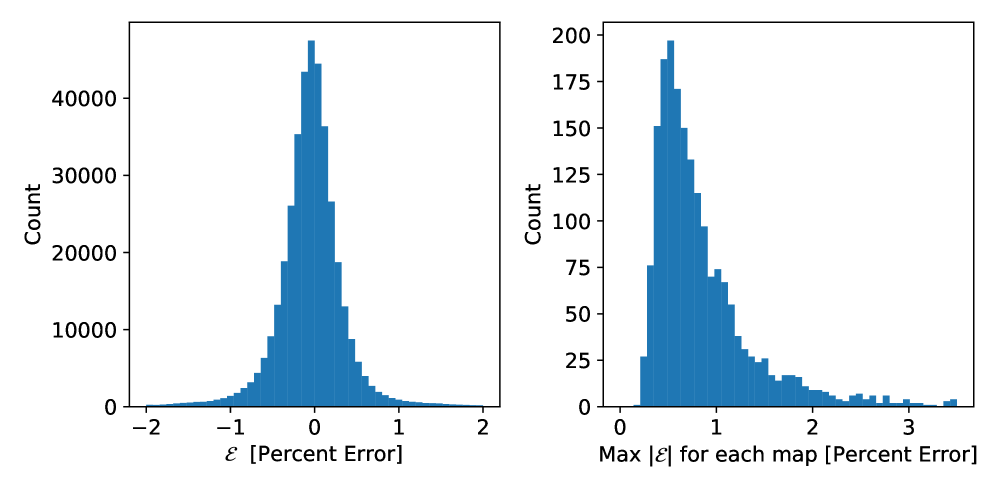
Обученная модель демонстрирует высокую точность восстановления карт вторых моментов, что является ключевым показателем для анализа движения звезд в галактиках. В ходе тестирования, отклонения в восстановленных данных составили от 2 до 6 километров в секунду, что соответствует погрешности менее 2-3%. Такая высокая точность позволяет детально изучать внутреннюю кинематику галактик, выявлять тонкие структуры и процессы, влияющие на их эволюцию. Возможность получения столь точных данных с минимальными погрешностями открывает новые перспективы для исследования динамики галактик и проверки существующих теоретических моделей.
Предложенный подход, основанный на анализе данных, демонстрирует беспрецедентную скорость обработки информации. В отличие от существующих методов, требующих значительных вычислительных ресурсов и времени, новая методика позволяет реконструировать динамические модели галактик приблизительно в 300 раз быстрее. Время инференса, то есть получения результата, составляет всего 0,3 миллисекунды, что открывает возможности для проведения крупномасштабных исследований и анализа огромных объемов данных в режиме реального времени. Такая эффективность делает возможным моделирование динамики галактик с беспрецедентной детализацией и точностью, значительно превосходящей возможности предыдущих поколений алгоритмов.
Исследования показали, что в девяти из десяти случаев максимальная погрешность при реконструкции динамических карт не превышает двух процентов. Такая высокая точность, достигнутая благодаря использованию нового подхода к моделированию, позволяет получать детальные представления о движении звёзд и газа в галактиках с беспрецедентной степенью достоверности. Низкий уровень ошибок гарантирует надежность полученных результатов и открывает возможности для проведения масштабных исследований, ранее затрудненных из-за ограничений в точности и вычислительной эффективности традиционных методов. Возможность получать столь точные результаты с минимальными погрешностями является ключевым фактором для дальнейшего развития астрофизического моделирования и анализа данных.
Традиционные методы моделирования динамики галактик часто опираются на ряд упрощающих предположений и эмпирических связей между наблюдаемой светимостью и невидимой динамикой. Эти предположения, хотя и позволяют проводить анализ, неизбежно вносят систематические смещения и ограничения в полученные результаты. В данном исследовании предложен подход, основанный на непосредственном обучении модели сопоставлению наблюдаемого распределения света с динамическими параметрами галактики. Это позволяет обойти необходимость в априорных предположениях о функциональной зависимости между светом и динамикой, минимизируя связанные с ними погрешности и позволяя получить более точную и объективную картину движения вещества в галактиках. В результате, модель способна выявлять сложные динамические структуры, которые могли оставаться незамеченными при использовании традиционных методов.
Достижение открывает новые возможности для эффективного и точного динамического моделирования галактик, позволяя проводить крупномасштабные исследования с беспрецедентной скоростью. Благодаря значительному ускорению процесса моделирования, астрономы теперь могут анализировать гораздо больше галактик и получать более надежные выводы об их структуре и эволюции. Это особенно важно для изучения формирования галактик, распределения темной материи и процессов, происходящих в ядрах галактик. Повышенная точность моделей позволяет минимизировать погрешности и получать более реалистичные представления о движении звезд и газа внутри галактик, что существенно улучшает понимание фундаментальных физических процессов, определяющих их развитие.
Исследование демонстрирует, как современные методы машинного обучения, в частности, нейронные сети, позволяют с высокой точностью моделировать динамику галактик. Подобный подход значительно превосходит традиционные методы по скорости вычислений, не уступая в качестве результатов. Это напоминает о том, как каждое измерение — это компромисс между стремлением к пониманию и реальностью, которая не желает быть понятой. Как заметил Нильс Бор: «Противоположности не противоречат друг другу, а дополняют». В данном случае, скорость и точность, долгое время казавшиеся взаимоисключающими, успешно сочетаются, открывая новые горизонты для изучения сложной динамики галактик и позволяя взглянуть на Вселенную, не заблудившись в её темноте.
Что впереди?
Представленная работа, подобно любому точному инструменту, лишь приоткрывает завесу над бездной. Ускорение динамического моделирования галактик посредством нейронных сетей — шаг, несомненно, важный, но он лишь демонстрирует, насколько примитивны «карманные чёрные дыры», которые мы строим для описания Вселенной. Уравнение Джинса, столь долгое время служившее ориентиром, по-прежнему требует утомительных вычислений, а предложенный подход, хоть и быстрый, лишь перекладывает сложность на обучение сети. Иногда материя ведёт себя так, как будто смеётся над нашими законами, и ускорение вычислений не отменяет необходимости понимания этого смеха.
Настоящий вызов заключается не в скорости, а в глубине. Будущие исследования должны быть направлены на преодоление ограничений, заложенных в самой архитектуре нейронных сетей. Возможно, потребуется разработка принципиально новых подходов, сочетающих в себе достоинства традиционных методов и возможности машинного обучения. Необходимо учитывать эффекты, которые остаются за рамками упрощённых моделей, такие как взаимодействие тёмной материи и барионной материи, нелинейные эффекты в динамике галактик, и влияние сверхмассивных чёрных дыр в центрах галактик.
И, пожалуй, самое главное — следует помнить, что каждая модель — это всего лишь приближение, каждая симуляция — лишь погружение в бездну. Истинная красота Вселенной заключается не в её предсказуемости, а в её непостижимости. И задача науки — не найти окончательные ответы, а научиться жить с вопросами.
Оригинал статьи: https://arxiv.org/pdf/2602.17371.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- SOL ПРОГНОЗ. SOL криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- FARTCOIN ПРОГНОЗ. FARTCOIN криптовалюта
- OM ПРОГНОЗ. OM криптовалюта
- SUI ПРОГНОЗ. SUI криптовалюта
2026-02-20 22:30