Байесовский вывод за счет симуляций: устойчивость к выбросам и эффективность

Автор: Денис Аветисян

В статье представлена новая методика байесовского вывода, основанная на симуляциях, которая обеспечивает надежность в условиях наличия выбросов и позволяет проводить быстрый и полностью автоматизированный анализ данных.

🐢

Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.

Телеграм канал

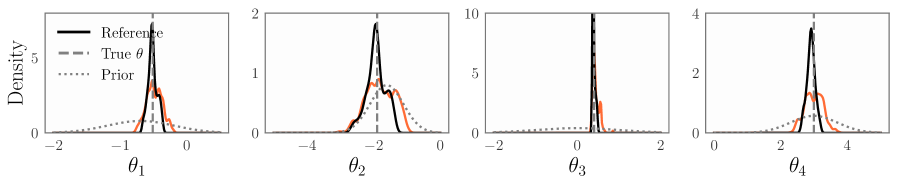
Эффективность алгоритмов NPL-MMD, ACE и GBI-SR демонстрирует устойчивый рост по мере увеличения вычислительных ресурсов, что указывает на перспективность дальнейшей оптимизации и масштабирования данных методов.

Предложен подход NSM-Bayes для устойчивого и эффективного байесовского вывода с использованием нейронных сетей и суррогатных функций правдоподобия.

Сложность современных симуляционных моделей часто сталкивается с чувствительностью к выбросам и экстремальным значениям в данных, возникающим из-за ошибок измерений. В данной работе, посвященной ‘Amortised and provably-robust simulation-based inference’, предложен новый подход к симуляционному выводу, основанный на обобщенном байесовском выводе и нейронной аппроксимации взвешенной функции соответствия оценок. Предложенный метод NSM-Bayes обеспечивает устойчивость к выбросам и позволяет реализовать эффективный, полностью амортизированный байесовский вывод с использованием нейронных сетей. Сможет ли данный подход существенно упростить сложные вычислительные задачи и открыть новые возможности для анализа данных в различных областях науки и техники?

Преодолевая Сложности Байесовского Вывода

Традиционные байесовские методы часто сталкиваются с проблемой неразрешимых функций правдоподобия, что существенно ограничивает их применимость к сложным симуляциям и моделям. Вычисление апостериорного распределения требует интегрирования произведения априорного распределения и функции правдоподобия, однако в случае сложных моделей эта интеграция может оказаться аналитически невозможной или вычислительно непосильной. Эта сложность возникает из-за высокой размерности пространства параметров или нелинейной структуры модели, что делает точное вычисление правдоподобия крайне затруднительным. В результате, исследователи вынуждены прибегать к приближенным методам, таким как метод Монте-Карло по цепям Маркова (MCMC) или вариационное приближение, которые, в свою очередь, могут вносить собственные погрешности и требовать значительных вычислительных ресурсов. Таким образом, преодоление проблемы неразрешимых функций правдоподобия является ключевой задачей для расширения возможностей байесовского вывода в различных областях науки и техники.

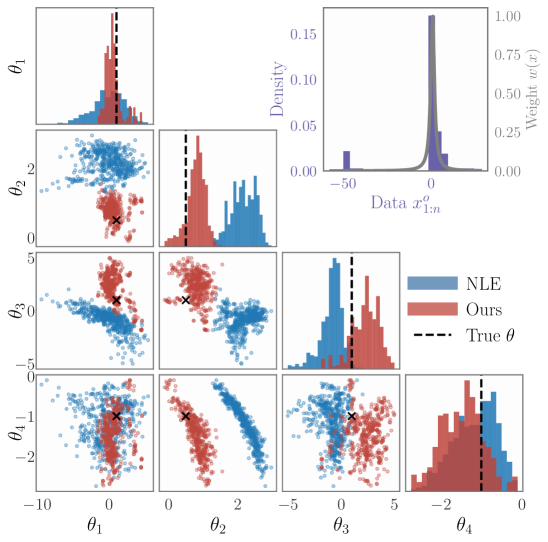
Традиционные байесовские методы, несмотря на свою элегантность, часто демонстрируют уязвимость к выбросам и неточностям в спецификации модели, что существенно ограничивает их надежность при применении к реальным данным. Исследования показывают, что даже незначительное количество аномальных значений — порядка 10% — может приводить к значительному смещению результатов, как это наблюдается в методе NLE (Non-Linear Estimation), что подтверждается данными, представленными на рисунке 1. Данное явление подчеркивает необходимость разработки более устойчивых методов байесовского вывода, способных эффективно справляться с неидеальностью данных и неопределенностью моделей, обеспечивая тем самым более точные и надежные оценки в практических приложениях.

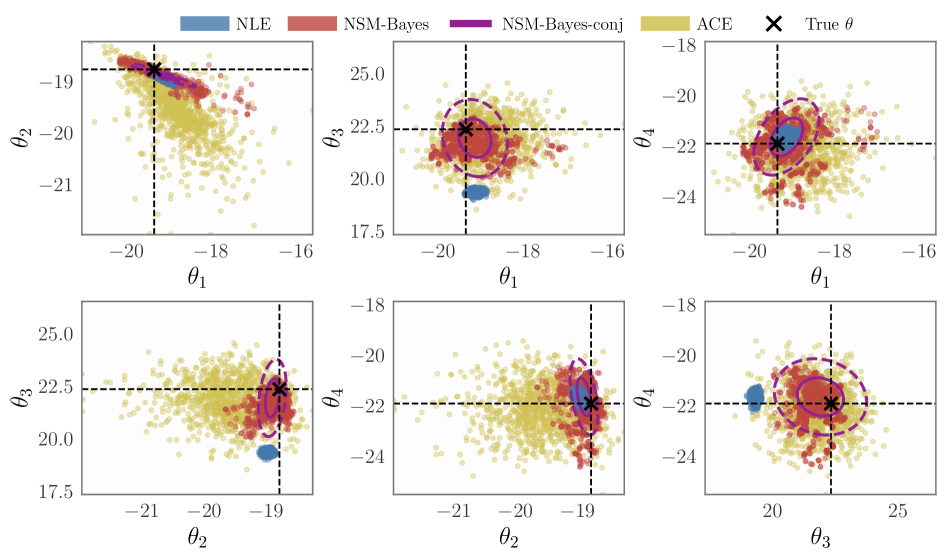
Сравнение методов оценки параметров модели радиораспространения при 10% выбросов показывает, что NLE сильно смещает оценки, в то время как NSM-Bayes и NSM-Bayes-conj обеспечивают более точные и устойчивые результаты, а ACE, хотя и демонстрирует смещение для <span class="katex-eq" data-katex-display="false"> heta_{2}</span>, хорошо работает для <span class="katex-eq" data-katex-display="false"> heta_{3}</span> и <span class="katex-eq" data-katex-display="false"> heta_{4}</span>, обеспечивая достаточно устойчивые оценки с повышенной неопределенностью, особенно для <span class="katex-eq" data-katex-display="false"> heta_{2}</span>. — Сравнение методов оценки параметров модели радиораспространения при 10% выбросов показывает, что NLE сильно смещает оценки, в то время как NSM-Bayes и NSM-Bayes-conj обеспечивают более точные и устойчивые результаты, а ACE, хотя и демонстрирует смещение для $heta_{2}$ , хорошо работает для $heta_{3}$ и $heta_{4}$ , обеспечивая достаточно устойчивые оценки с повышенной неопределенностью, особенно для $heta_{2}$ .

NSM-Bayes: Устойчивый Вывод через Сопоставление Оценок

Метод NSM-Bayes представляет собой мощный фреймворк для байесовского вывода, использующий симуляцию для аппроксимации апостериорного распределения. В отличие от традиционных методов, NSM-Bayes не требует явного задания функции правдоподобия $p(\text{data}|\text{parameters})$ . Вместо этого, он напрямую моделирует градиент логарифма апостериорного распределения, используя симулированные данные и оптимизируя параметры модели с помощью методов стохастического градиентного спуска. Такой подход позволяет проводить байесовский вывод в сложных моделях, где вычисление или аналитическое выражение функции правдоподобия затруднено или невозможно, обеспечивая гибкость и расширяя возможности применения байесовских методов.

Метод NSM-Bayes демонстрирует повышенную устойчивость к выбросам и неверной спецификации модели благодаря использованию техник сопоставления оценок (score matching). Экспериментальная оценка производительности на различных задачах, включая распределение g-and-k, модель SIR эпидемий и симулятор распространения радиосигнала, подтверждает эту устойчивость. В частности, сопоставление оценок позволяет эффективно оценивать параметры модели даже при наличии зашумленных данных или отклонениях от предполагаемого вида распределения, что обеспечивает более надежные результаты по сравнению с традиционными методами байесовского вывода, требующими точного знания функции правдоподобия.

Метод NSM-Bayes использует специально разработанную функцию потерь для обеспечения стабильного обучения. Данная функция потерь состоит из двух ключевых компонентов: следа гессиана и градиента функции взвешивания. След гессиана обеспечивает контроль над кривизной функции потерь, способствуя более быстрому и стабильному сходимости алгоритма. Градиент функции взвешивания, в свою очередь, корректирует вклад различных параметров в процессе обучения, предотвращая переобучение и повышая устойчивость к выбросам. Комбинация этих двух компонентов позволяет NSM-Bayes эффективно обучаться даже при наличии шума в данных или неточностях в модели. Математически, функция потерь может быть представлена как $L = Tr(H) + \nabla w(x)$ , где $H$ — гессиан, $w(x)$ — функция взвешивания, а $Tr$ обозначает след матрицы.

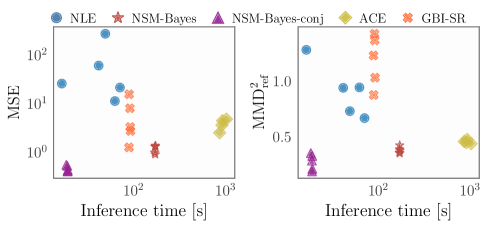
В условиях неполных данных и зашумлений, алгоритм NSM-Bayes-conj демонстрирует наилучшую производительность при минимальных затратах времени по сравнению с моделями <span class="katex-eq" data-katex-display="false">NLE</span>, <span class="katex-eq" data-katex-display="false">NSM-Bayes</span>, <span class="katex-eq" data-katex-display="false">GBI-SR</span> и <span class="katex-eq" data-katex-display="false">ACE</span>. — В условиях неполных данных и зашумлений, алгоритм NSM-Bayes-conj демонстрирует наилучшую производительность при минимальных затратах времени по сравнению с моделями $NLE$ , $NSM-Bayes$ , $GBI-SR$ и $ACE$ .

NSM-Bayes-conj: Эффективность через Ограничение Сети

Метод NSM-Bayes-conj является расширением базового метода NSM-Bayes, достигаемым за счет ограничения формы используемой нейронной сети. Данное ограничение позволяет использовать сопряженные апостериорные обновления $p(\theta|x) \propto p(x|\theta)p(\theta)$ , где θ — параметры модели, $x$ — данные. Использование сопряженных распределений упрощает вычисление апостериорного распределения, избегая необходимости в сложных приближениях или итеративных вычислениях, что значительно повышает скорость и эффективность алгоритма.

Ограничение формы сети в методе NSM-Bayes-conj существенно повышает вычислительную эффективность за счет возможности использования сопряженных обновлений апостериорного распределения. Вместо итеративных численных методов, требующих значительных ресурсов, сопряженное обновление позволяет аналитически рассчитать апостериорное распределение, что снижает вычислительную сложность с $O(N^3)$ до $O(N)$ , где N — размерность задачи. Это упрощение делает метод NSM-Bayes-conj применимым к задачам высокой размерности, которые были бы недоступны для стандартного NSM-Bayes из-за ограничений по вычислительным ресурсам и времени.

Метод амортизированного вывода (Amortised Inference) является неотъемлемой частью как NSM-Bayes, так и NSM-Bayes-conj. Вместо повторного выполнения вывода для каждой новой точки данных, амортизированный вывод обучает модель, аппроксимирующую апостериорное распределение. Это позволяет быстро оценивать апостериорное распределение для новых входных данных, используя обученную модель. Фактически, это снижает вычислительную сложность, заменяя итеративные процедуры вывода на однократный проход через обученную сеть, обеспечивая значительное ускорение процесса аппроксимации апостериорного распределения $p(θ|x)$ , где θ — параметры модели, а $x$ — входные данные.

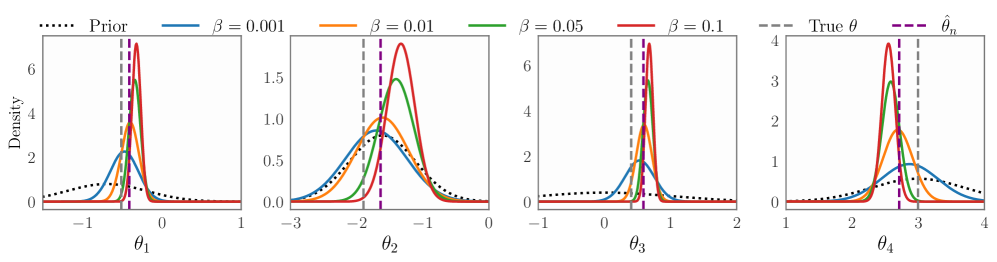
Изменение скорости обучения <span class="katex-eq" data-katex-display="false">eta</span> в алгоритме NSM-Bayes-conj позволяет оптимизировать оценку занижения заболеваемости в модели SIR. — Изменение скорости обучения $eta$ в алгоритме NSM-Bayes-conj позволяет оптимизировать оценку занижения заболеваемости в модели SIR.

Применимость и Влияние Предложенного Фреймворка

Эффективность методов NSM-Bayes и NSM-Bayes-conj была подтверждена посредством тестирования на разнообразных наборах данных, демонстрирующих их универсальность и надежность. Исследования охватили различные области: от статистического моделирования, представленного распределением g-and-k, до динамических систем, моделируемых с помощью SIR-модели эпидемий, и задач распространения радиосигнала, симулируемых специализированным программным обеспечением. Полученные результаты свидетельствуют о способности данных методов успешно решать задачи оценки параметров и количественной оценки неопределенности в широком спектре научных дисциплин, что подтверждает их значимость как передового подхода к надежному байесовскому выводу.

Успех методов NSM-Bayes и NSM-Bayes-conj в различных областях науки напрямую связан с применением вычислений, основанных на симуляциях, и усиленных возможностями нейронных сетей. Этот подход позволяет оценивать параметры и квантифицировать неопределенности в сложных моделях, обходя ограничения традиционных аналитических методов. Нейронные сети, обученные на результатах симуляций, эффективно аппроксимируют апостериорные распределения, что значительно ускоряет процесс вывода и позволяет работать с моделями, для которых получение аналитических решений невозможно. Такой симбиоз симуляций и нейронных сетей открывает новые горизонты в научной моделировании, обеспечивая надежный и эффективный инструмент для анализа данных и принятия решений в различных дисциплинах, от эпидемиологии до радиосвязи.

Развитие методов NSM-Bayes и NSM-Bayes-conj открывает новые горизонты в области научного моделирования, оценки параметров и количественной оценки неопределенностей. Данные подходы, основанные на симуляционном выводе с применением нейронных сетей, демонстрируют высокую эффективность в различных дисциплинах — от эпидемиологического моделирования до радиосвязи. Они представляют собой передовой инструмент для получения надежных байесовских оценок, особенно в сложных задачах, где традиционные методы оказываются неэффективными или требуют значительных вычислительных ресурсов. Эта технология позволяет исследователям более точно описывать и прогнозировать поведение систем, а также учитывать связанные с этим риски и неопределенности, что делает ее незаменимой для принятия обоснованных решений в различных областях науки и техники.

Нейронная оценка правдоподобия (NLE) чувствительна к выбросам в данных, что существенно влияет на параметры, определяющие масштаб и асимметрию распределения, в то время как предложенный нами метод, основанный на сопоставлении нейронных оценок (neural score-matching Bayes), демонстрирует устойчивость благодаря функции взвешивания <span class="katex-eq" data-katex-display="false">w(x)</span>, снижающей влияние этих выбросов. — Нейронная оценка правдоподобия (NLE) чувствительна к выбросам в данных, что существенно влияет на параметры, определяющие масштаб и асимметрию распределения, в то время как предложенный нами метод, основанный на сопоставлении нейронных оценок (neural score-matching Bayes), демонстрирует устойчивость благодаря функции взвешивания $w(x)$ , снижающей влияние этих выбросов.

Представленная работа демонстрирует, что эффективные методы вывода не требуют жесткого проектирования, а скорее возникают из локальных правил, заложенных в симуляции. NSM-Bayes, предложенный подход, подтверждает эту идею, обеспечивая устойчивость к выбросам и возможность полностью амортизированного байесовского вывода. Это согласуется с принципом самоорганизации, где система обретает порядок не через внешнее управление, а благодаря внутренним взаимодействиям. Как заметил Ральф Уолдо Эмерсон: «В каждой внешней задаче скрыта внутренняя возможность». Именно эта внутренняя возможность, раскрытая через адаптацию к данным и устойчивость к аномалиям, позволяет NSM-Bayes эффективно решать задачи байесовского вывода, избегая иллюзии полного контроля и фокусируясь на реальном влиянии локальных правил.

Куда же дальше?

Представленная работа, демонстрируя устойчивость к выбросам в задачах байесовского вывода, лишь подчеркивает фундаментальную истину: шум неизбежен. Попытки полного контроля над случайностью — иллюзия, а эффективное влияние — в умении работать с непредсказуемостью. Развитие методов, подобных NSM-Bayes, не столько о создании идеальных моделей, сколько о разработке механизмов, позволяющих системе адаптироваться к неполноте и искажениям входных данных.

Очевидным направлением дальнейших исследований представляется ослабление предположений о структуре данных. Большинство существующих подходов, включая и данный, подразумевают некоторую степень гладкости или регулярности. Исследование устойчивости к произвольным, неструктурированным помехам, а также разработка методов, способных самостоятельно выявлять и учитывать подобные искажения, представляется задачей, требующей пристального внимания. В конечном итоге, порядок возникает не из архитектуры, а из локальных правил, и задача исследователя — выявить эти правила в хаосе.

Наконец, стоит задуматься о масштабируемости предложенного подхода к задачам, где количество параметров модели значительно превосходит объем доступных данных. В таких условиях, даже устойчивые к выбросам методы могут столкнуться с проблемами переобучения. Разработка эффективных механизмов регуляризации и отбора признаков, учитывающих специфику байесовского вывода, представляется ключевым направлением для обеспечения надежности и обобщающей способности подобных систем.

Оригинал статьи: https://arxiv.org/pdf/2602.11325.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-15 15:45