Градиенты Больших Языковых Моделей: Новый Взгляд на Оптимизацию

Автор: Денис Аветисян

Исследование выявило особенности структуры градиентов в больших языковых моделях и предлагает новый подход к оптимизации, направленный на повышение скорости обучения и качества результатов.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Телеграм канал

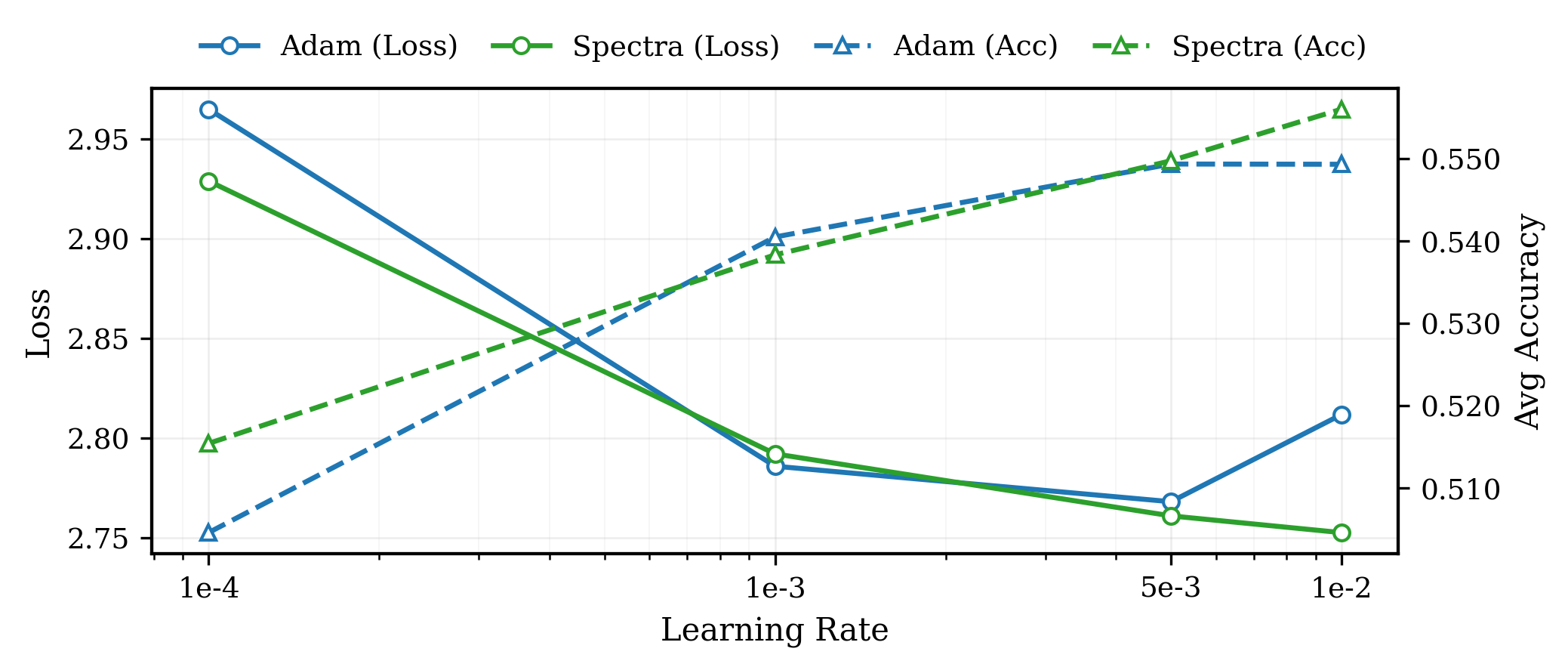
В ходе исследования сравнивались алгоритмы оптимизации Spectra и AdamW при различных значениях скорости обучения <span class="katex-eq" data-katex-display="false"> \eta \in \{8 \times 10^{-4}, 1 \times 10^{-3}, 5 \times 10^{-3}, 1 \times 10^{-2} \} </span>, при этом Spectra продемонстрировала более быструю сходимость и превосходные результаты в большинстве режимов обучения. — В ходе исследования сравнивались алгоритмы оптимизации Spectra и AdamW при различных значениях скорости обучения $\eta \in \{8 \times 10^{-4}, 1 \times 10^{-3}, 5 \times 10^{-3}, 1 \times 10^{-2} \}$ , при этом Spectra продемонстрировала более быструю сходимость и превосходные результаты в большинстве режимов обучения.

В статье представлен оптимизатор Spectra, использующий селективное ослабление доминирующего пика в спектре градиентов, что позволяет избежать усиления шумовой составляющей и улучшить сходимость.

Несмотря на значительные успехи в обучении больших языковых моделей (LLM), асимметрия градиентов, проявляющаяся в доминировании низкоранговых направлений и подавлении «хвоста», остаётся малоизученной проблемой. В статье ‘Spectra: Rethinking Optimizers for LLMs Under Spectral Anisotropy’ авторы анализируют эту анизотропию спектра градиентов и предлагают новый оптимизатор Spectra, который выборочно ослабляет доминирующий «пик», избегая усиления чувствительного к шуму «хвоста». Показано, что Spectra позволяет ускорить сходимость обучения LLaMA3 8B на 30% по сравнению с AdamW, снизить потребление памяти состояния оптимизатора на 49.25% и улучшить точность на downstream задачах на 1.62%. Не откроет ли эта стратегия низкоранговой адаптации новые горизонты в разработке эффективных и ресурсосберегающих алгоритмов обучения LLM?

Анизотропия Градиентов: Почему LLM Учатся Неэффективно

Обучение больших языковых моделей, несмотря на свою впечатляющую эффективность, характеризуется выраженной анизотропией градиентных сигналов, что приводит к формированию неравномерного ландшафта оптимизации. Вместо равномерного распределения, градиенты, направляющие процесс обучения, концентрируются в определенных направлениях, создавая “пики” и “долины” в пространстве параметров модели. Это означает, что некоторые параметры обновляются значительно быстрее и интенсивнее, чем другие, что может приводить к неэффективному использованию вычислительных ресурсов и замедлению сходимости. Такая неравномерность существенно влияет на способность модели обобщать информацию и адаптироваться к новым данным, поскольку некоторые аспекты обучения могут быть недостаточно представлены в процессе оптимизации. Понимание природы этой анизотропии является ключевым для разработки более эффективных стратегий обучения и повышения устойчивости больших языковых моделей.

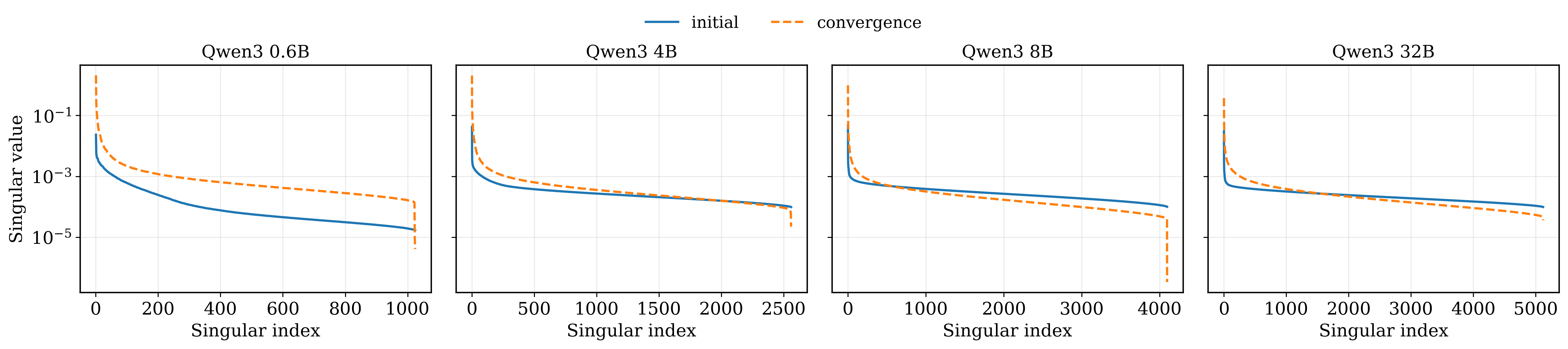
Анализ градиентного спектра больших языковых моделей выявил выраженную анизотропию, проявляющуюся в виде доминирующего “низкорангового пика”. Этот пик указывает на то, что обновления параметров модели концентрируются в относительно небольшом числе направлений в пространстве параметров. По сути, обучение становится сильно смещенным, поскольку большая часть градиентного сигнала направлена лишь на изменение небольшой подмножества весов, игнорируя или подавляя более тонкие, но потенциально важные вариации в данных. Такая концентрация обновления может ограничивать способность модели к обобщению и адаптации к новым, не встречавшимся ранее ситуациям, поскольку важные направления в пространстве параметров, представленные в “хвосте” спектра, остаются недостаточно задействованными в процессе обучения.

В процессе обучения больших языковых моделей (LLM) наблюдается явление, когда доминирующий “низкоранговый пик” в спектре градиентов непропорционально усиливает обновления параметров. Это приводит к тому, что обучение становится смещенным в сторону наиболее распространенных семантических вариаций, в то время как “хвостовой спектр”, представляющий собой менее частые, но потенциально важные нюансы языка, подавляется. Фактически, модель может упускать из виду редкие, но критически важные закономерности в данных, что ограничивает её способность к обобщению и адаптации к новым, нетипичным ситуациям. Данное явление подчеркивает необходимость разработки новых стратегий оптимизации, способных эффективно использовать информацию, содержащуюся во всем спектре градиентов, а не только в его доминирующей части.

Понимание спектральной предвзятости градиентов имеет решающее значение для разработки более эффективных и устойчивых стратегий оптимизации больших языковых моделей. Исследования показывают, что доминирующий «низкоранговый пик» в спектре градиентов концентрирует обновления в ограниченном числе направлений, потенциально подавляя обучение в «хвостовом спектре», представляющем менее частые семантические вариации. Анализ этой предвзятости позволяет создавать алгоритмы, которые более равномерно распределяют усилия по обучению, охватывая более широкий спектр лингвистических нюансов и повышая обобщающую способность модели. Таким образом, учитывая спектральную структуру градиентов, можно существенно улучшить процесс обучения, добиваясь более быстрых результатов и создавая модели, устойчивые к различным типам входных данных и задачам.

Спектры сингулярных чисел градиента MLP в самых глубоких слоях моделей Qwen3 (от 0.6B до 32B) на различных этапах обучения демонстрируют устойчивый профиль «пик низкой ранговой части + гладкий хвост», где сингулярные значения пика отделены от хвоста примерно на 1-2 порядка величины и занимают около 1.5% направлений.

Механизмы Спектральной Предвзятости: Почему Так Происходит?

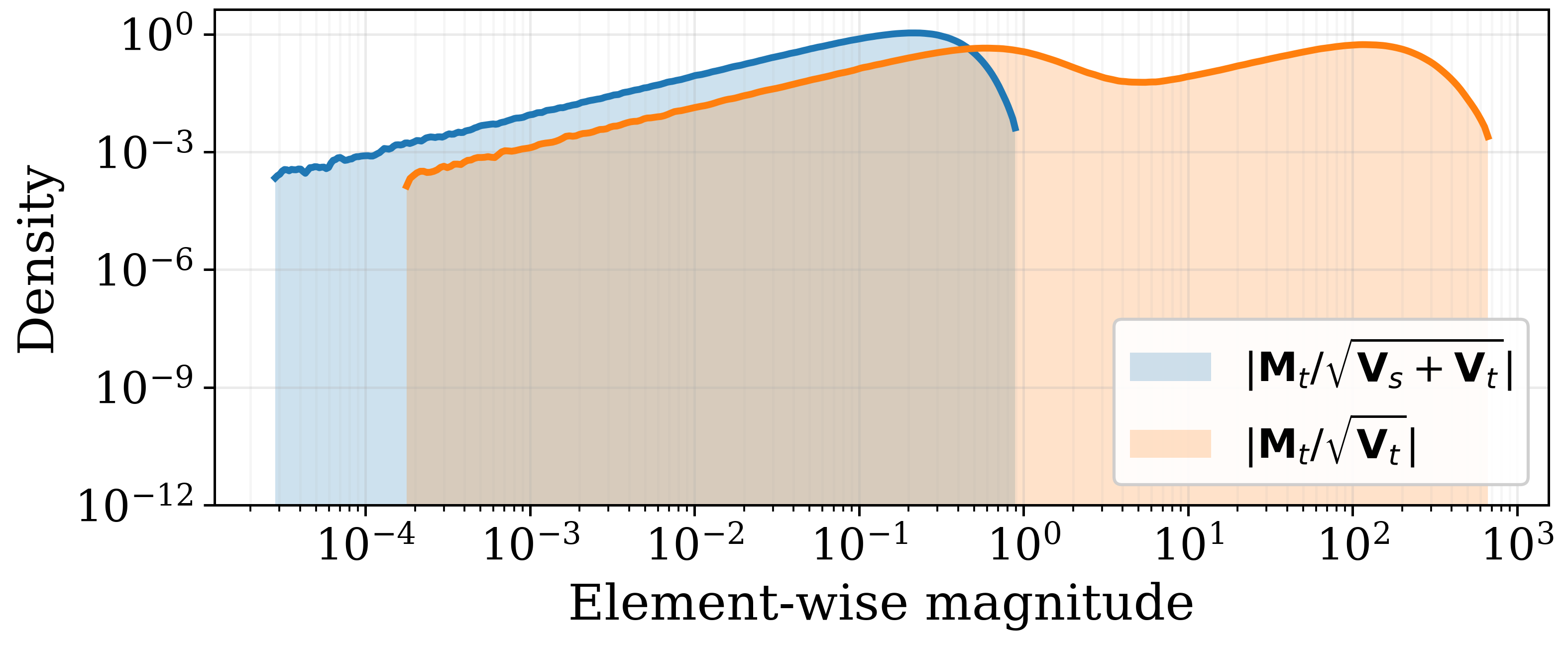
Наблюдаемые доминирующие обновления в процессе оптимизации частично обусловлены механикой оптимизатора AdamW и его использованием накопления вторых моментов. В частности, AdamW поддерживает оценки первого и второго моментов градиентов для каждого параметра. Накопление второго момента, $v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$ , где $g_t$ — градиент, а $\beta_2$ — коэффициент затухания, приводит к тому, что параметры с большими градиентами получают непропорционально большее обновление, что способствует формированию “пиков” в направлении обновления. Это особенно заметно в задачах с разреженными градиентами или в поздних стадиях обучения, когда градиенты могут быть сосредоточены в небольшом количестве измерений, усиливая эффект накопления второго момента.

Численные методы, применяемые в спектральной обработке, такие как итерация Ньютона-Шульца, могут вносить ‘численную дисперсию’ (numerical variance). Эта дисперсия возникает из-за ошибок округления и накопления при выполнении итеративных вычислений. Особенностью является то, что данная дисперсия непропорционально влияет на ‘хвост’ спектра — область малых сингулярных чисел. Это происходит потому, что небольшие изменения в данных, вызванные численной дисперсией, сильнее проявляются в компонентах с низкой энергией, что приводит к искажению информации в хвосте спектра и снижению надежности направлений, соответствующих этим компонентам. Анализ дисперсии позволяет оценить чувствительность спектральных компонентов к численным ошибкам.

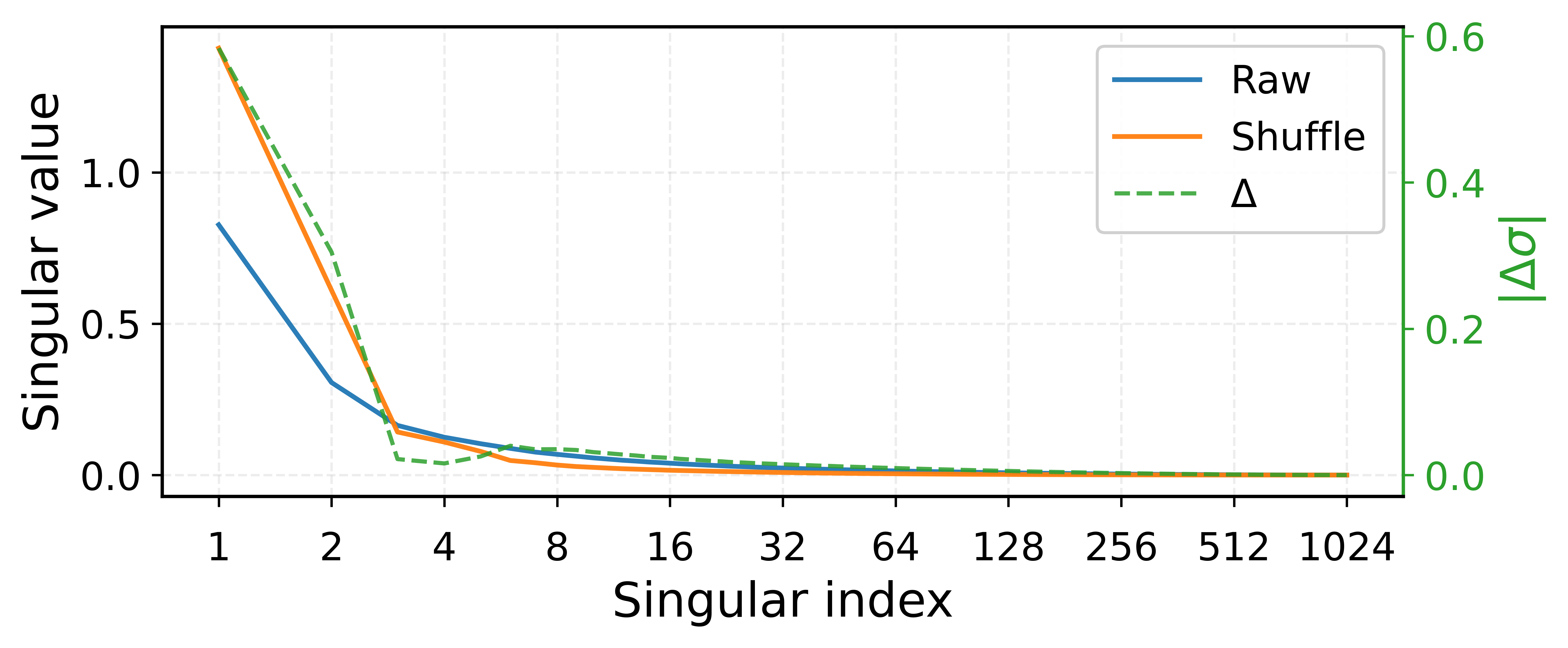
Надежность направлений в «хвосте» спектра, то есть областей с малыми сингулярными числами, количественно оценивается их «относительным разбросом» (relative variance). Этот показатель отражает чувствительность конкретного направления к шуму и численным погрешностям. Высокий относительный разброс указывает на то, что направление может быть нестабильным и не отражает истинные характеристики данных, а является артефактом численных методов. Таким образом, при анализе спектра необходимо учитывать относительный разброс направлений, особенно в «хвосте», для оценки достоверности результатов и исключения ложных положительных результатов при интерпретации данных. $\sigma_{rel} = \frac{\sigma_i}{\mu_i}$ , где $\sigma_i$ — стандартное отклонение, а $\mu_i$ — среднее значение, характеризующее разброс вокруг конкретного направления.

Спектральный анализ, в частности, с использованием сингулярного разложения (SVD), является ключевым методом для выявления и количественной оценки спектральных характеристик данных, возникающих в процессе обучения нейронных сетей. SVD позволяет декомпозировать матрицу, представляющую градиенты или веса, на компоненты, упорядоченные по величине собственных значений. Эти собственные значения отражают важность соответствующих направлений в пространстве параметров, а сингулярные векторы — соответствующие направления. Анализ распределения собственных значений позволяет определить доминирующие и слабовыраженные направления, выявить потенциальные проблемы, такие как низкоранговость или наличие зашумленных направлений, и оценить чувствительность к изменениям в данных или параметрах обучения. Количественная оценка этих характеристик необходима для понимания механизмов спектральной предвзятости и разработки стратегий ее смягчения.

В модели Qwen3-0.6B доминирование импульсов во втором моменте приводит к подавлению обновлений в хвосте распределения, что проявляется в большей концентрации энергии второго момента <span class="katex-eq" data-katex-display="false">\mathbf{V}</span> по сравнению с первым моментом <span class="katex-eq" data-katex-display="false">\mathbf{M}</span> и значительному сокращению величины обновлений при нормализации с учетом как старых, так и текущих моментов. — В модели Qwen3-0.6B доминирование импульсов во втором моменте приводит к подавлению обновлений в хвосте распределения, что проявляется в большей концентрации энергии второго момента $\mathbf{V}$ по сравнению с первым моментом $\mathbf{M}$ и значительному сокращению величины обновлений при нормализации с учетом как старых, так и текущих моментов.

Spectra Optimizer: Новый Подход к Балансировке Градиентов

Оптимизатор ‘Spectra’ представляет собой новый алгоритм, разработанный для снижения влияния доминирующего низкорангового ‘пика’ (spike) в градиентах во время обучения больших языковых моделей. Основная задача алгоритма — ослабить этот доминирующий пик, который может приводить к нестабильности и замедлению сходимости, при этом сохраняя информацию, содержащуюся в ‘хвосте’ спектра градиентов — то есть, в менее значимых компонентах. Такой подход позволяет добиться более сбалансированного процесса оптимизации, эффективно используя информацию из всех компонент градиента, а не только из доминирующей.

Эффективная оценка подпространства доминирующего спайка достигается за счет использования «warm-started power iteration» — итерационного метода, инициализируемого теплой отправной точкой для ускорения сходимости. Этот метод позволяет оперативно определить направления, в которых градиенты наиболее выражены. Одновременно, для калибровки размера шага оптимизации применяется «RMS normalization» — нормализация среднеквадратичного значения градиентов. Такой подход позволяет динамически адаптировать размер шага в зависимости от величины градиента, предотвращая перерегулирование и обеспечивая более стабильный процесс оптимизации. Комбинация этих двух методов позволяет Spectra Optimizer эффективно справляться с задачами балансировки градиентов и ускорять обучение моделей.

Оптимизатор Spectra изменяет направление обновления параметров, чтобы снизить влияние доминирующих низкоранговых «пиков» в градиенте. Традиционные оптимизаторы часто подвержены эффекту, когда единичные параметры значительно изменяются из-за крупных градиентов, что приводит к нестабильности и замедлению сходимости. Spectra решает эту проблему, переформатируя вектор обновления, что позволяет более равномерно распределить вклад различных параметров и способствует более сбалансированному процессу оптимизации. Это позволяет избежать чрезмерного влияния отдельных параметров и улучшить общую эффективность обучения модели.

Предварительные результаты тестирования алгоритма Spectra Optimizer показали значительное улучшение производительности. На модели LLaMA3-8B зафиксировано ускорение обучения на 30%, снижение объема памяти, необходимого для хранения состояния оптимизатора, на 49.25%, и повышение средней точности на downstream задачах на 1.62% по сравнению с AdamW. На той же модели LLaMA3-8B конечная функция потерь снизилась на 1.5%, а время выполнения одного шага оптимизации на Qwen3-0.6B сократилось на 0.7%. Кроме того, на модели Qwen3-0.6B алгоритм Spectra продемонстрировал 5.1-кратное увеличение пропускной способности по сравнению с Muon.

Применяя частотно-нормализованное подавление (<span class="katex-eq" data-katex-display="false">FreqNorm</span>) и перемешивание токенов внутри предложений (<span class="katex-eq" data-katex-display="false">Shuffle</span>) к LLaMA3-8B, можно избирательно подавлять или усиливать доминирующие частотные компоненты градиента, при этом изменения быстро затухают в конце спектра. — Применяя частотно-нормализованное подавление ( $FreqNorm$ ) и перемешивание токенов внутри предложений ( $Shuffle$ ) к LLaMA3-8B, можно избирательно подавлять или усиливать доминирующие частотные компоненты градиента, при этом изменения быстро затухают в конце спектра.

Влияние и Перспективы для Оптимизации LLM

Оптимизатор “Спектра” представляет собой перспективный подход к повышению эффективности и устойчивости обучения больших языковых моделей (LLM), особенно тех, которые требуют глубокого понимания семантики. В отличие от традиционных методов, которые могут испытывать трудности с балансировкой различных частотных компонентов в процессе обучения, “Спектра” фокусируется на корректировке спектрального дисбаланса, что позволяет модели более эффективно усваивать сложные взаимосвязи между словами и понятиями. Это, в свою очередь, может привести к повышению точности, снижению вычислительных затрат и улучшению обобщающей способности модели, делая её более надежной и применимой к широкому спектру задач, требующих нюансированного анализа текста и понимания контекста.

Исследование показывает, что устранение спектрального дисбаланса в процессе обучения больших языковых моделей (LLM) открывает значительные возможности для повышения их производительности и снижения вычислительных затрат. Традиционные методы оптимизации часто игнорируют неравномерное распределение энергии сигнала по частотам, что приводит к неэффективному использованию вычислительных ресурсов и замедляет сходимость обучения. Коррекция этого дисбаланса позволяет более эффективно использовать доступные вычислительные мощности, ускоряя процесс обучения и, как следствие, снижая его стоимость. Потенциально, это также может привести к созданию моделей с улучшенным пониманием нюансов семантики и более точными результатами, поскольку обучение становится более стабильным и сфокусированным на наиболее важных аспектах данных. В конечном итоге, решение проблемы спектрального дисбаланса является ключевым шагом к разработке более устойчивых и масштабируемых подходов к обучению LLM.

Дальнейшие исследования будут направлены на глубокое изучение теоретических основ спектральной оптимизации. Ученые планируют всесторонне проанализировать, каким образом балансировка спектральных характеристик влияет на сходимость обучения и обобщающую способность больших языковых моделей. Особое внимание будет уделено применению данного подхода к различным архитектурам, включая трансформеры и рекуррентные нейронные сети, а также к разнообразным наборам данных, представляющим различные языки и предметные области. Целью является не только повышение эффективности обучения, но и выявление универсальных принципов, которые позволят адаптировать спектральную оптимизацию к широкому спектру задач искусственного интеллекта, способствуя созданию более устойчивых и масштабируемых моделей.

Данное исследование открывает перспективы для разработки более экологичных и масштабируемых методов обучения больших языковых моделей. Традиционные подходы к обучению требуют значительных вычислительных ресурсов и энергозатрат, что ограничивает доступ к этой мощной технологии. Потенциал снижения вычислительной сложности и повышения эффективности обучения, достигаемый благодаря новым оптимизационным стратегиям, позволит значительно уменьшить “углеродный след” и сделать передовые языковые модели доступными для более широкого круга исследователей и организаций, способствуя дальнейшему развитию искусственного интеллекта и расширению его применения в различных областях знаний и практической деятельности.

Применение методов нормализации частоты (<span class="katex-eq" data-katex-display="false">FreqNorm</span>) и перемешивания токенов (<span class="katex-eq" data-katex-display="false">Shuffle</span>) позволяет избирательно подавлять или усиливать доминирующие частотные компоненты в модели Qwen3-0.6B, при этом изменения быстро затухают в дальнем спектре. — Применение методов нормализации частоты ( $FreqNorm$ ) и перемешивания токенов ( $Shuffle$ ) позволяет избирательно подавлять или усиливать доминирующие частотные компоненты в модели Qwen3-0.6B, при этом изменения быстро затухают в дальнем спектре.

Исследование градиентной анизотропии в больших языковых моделях неизбежно наводит на мысль о хрупкости любой оптимизации. Авторы предлагают Spectra, пытаясь обуздать «доминирующий пик» градиента, но в этом стремлении к контролю кроется парадокс. Как гласит известная фраза Марвина Мински: «Наиболее полезная вещь, которую мы можем сделать, — это найти проблему, которую мы действительно хотим решить». В данном случае, проблема не только в скорости сходимости, но и в фундаментальном понимании того, как эти градиенты формируются. Любая попытка «приглушить» аномалии, как показывает практика, рано или поздно требует компенсации, а значит, и нового раунда борьбы с последствиями. Архитектура оптимизатора, как и любая архитектура, — это компромисс, переживший деплой.

Что дальше?

Работа, безусловно, выявила закономерность в хаосе градиентов больших языковых моделей — этот упрямый «хвост» в спектре, который, как и все долги, рано или поздно требует погашения. Spectra пытается его приглушить, и, вероятно, на какое-то время это сработает. Но не стоит обольщаться: каждый «революционный» оптимизатор, рано или поздно, превращается в техдолг, требующий всё более сложных патчей и обходных путей. Вопрос не в том, чтобы найти идеальный оптимизатор, а в том, как долго можно откладывать рефакторинг архитектуры, которая порождает эти самые анизотропные градиенты.

Следующим шагом, очевидно, станет попытка обобщить подход. Сработает ли Spectra с моделями, которые в десять раз больше? Не потребует ли она ещё более тонкой настройки, превратившись в чёрный ящик, управляемый эвристиками? И, что самое главное, не окажется ли, что это всего лишь временное облегчение симптомов, а не решение фундаментальной проблемы? Ведь рано или поздно, даже самые изящные трюки с градиентами не смогут скрыть тот факт, что мы пытаемся обучить монстра, чьё внутреннее устройство остаётся загадкой.

И, напоследок, стоит задуматься о более радикальном подходе. Вместо того, чтобы бороться с анизотропией, нельзя ли её использовать? Может быть, эта «странность» градиентов — не баг, а фича, позволяющая моделям учиться более эффективно, пусть и непредсказуемым образом? Автоматизация, конечно, спасёт нас, но сначала она наверняка удалит прод.

Оригинал статьи: https://arxiv.org/pdf/2602.11185.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-15 10:59