Автор: Денис Аветисян
Новый подход позволяет оценить плотность транспортного потока, используя лишь начальные и конечные позиции отдельных автомобилей.
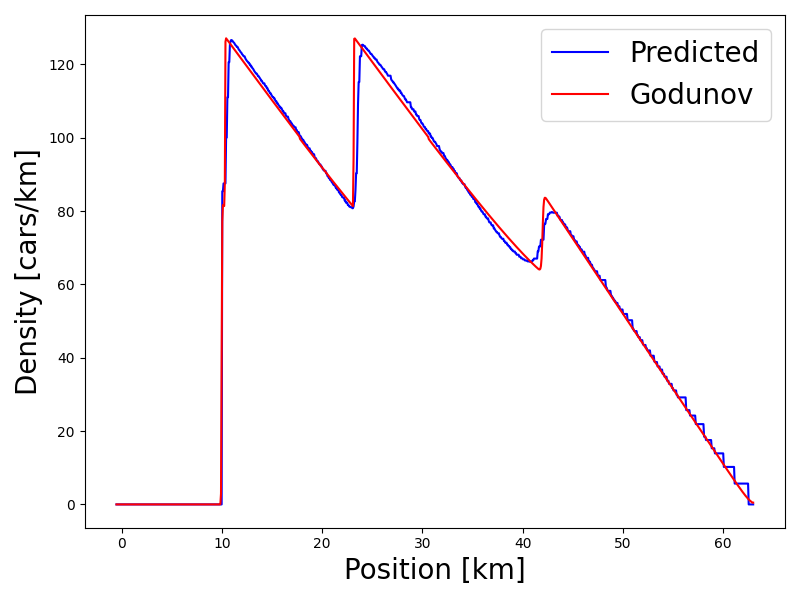
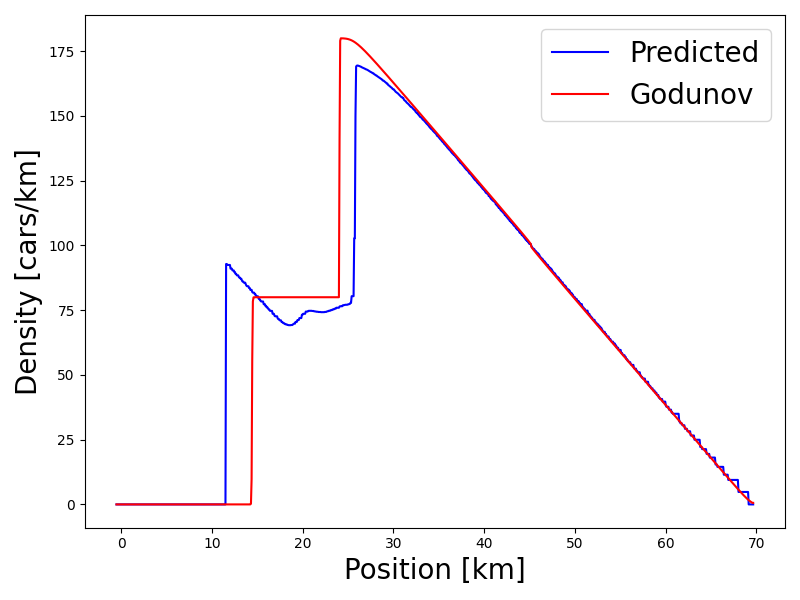
В работе предложен метод машинного обучения для реконструкции плотности трафика, основанный на сближении макро— и микроскопических моделей, не требующий явного обеспечения законов сохранения.
Восстановление плотности транспортного потока по ограниченным данным представляет собой сложную задачу, особенно при низкой доле оснащенных зондов. В настоящей работе, ‘Traffic Flow Reconstruction from Limited Collected Data’, предлагается эффективный метод реконструкции плотности, основанный на данных о начальном и конечном положениях небольшого числа транспортных средств, полученных с помощью микроскопических динамических систем. Разработанный машинный алгоритм позволяет приблизительно оценить плотность потока, демонстрируя сходимость к известным макроскопическим моделям при увеличении числа исследуемых автомобилей. Способно ли данное сочетание микро- и макроскопического подходов открыть новые горизонты в моделировании транспортных потоков и управлении дорожным движением?
Точная Модель Транспортного Потока: Основы и Принципы
Точное моделирование состояния транспортного потока — плотности, скорости и пропускной способности — является фундаментальной задачей для эффективного управления и прогнозирования дорожной обстановки. Эти три параметра неразрывно связаны между собой: увеличение плотности транспортных средств обычно приводит к снижению средней скорости, а также влияет на общую пропускную способность дороги. Игнорирование даже одного из этих показателей может привести к неточным прогнозам заторов, неэффективному распределению ресурсов и, как следствие, к ухудшению транспортной ситуации в целом. Современные системы управления трафиком используют сложные математические модели и алгоритмы, основанные на непрерывном мониторинге этих параметров, для оптимизации дорожных потоков, уменьшения времени в пути и повышения безопасности дорожного движения. Q = \rho \cdot v — эта простая формула, связывающая пропускную способность (Q), плотность (ρ) и скорость (v), иллюстрирует важность точного определения каждого из этих параметров для адекватного анализа и управления транспортными потоками.
В основе теории транспортных потоков лежит фундаментальная связь между плотностью транспортного потока и средней скоростью движения. Эта зависимость, часто описываемая моделью Гриншилда, демонстрирует нелинейный характер трафика: с увеличением плотности транспортных средств, средняя скорость сначала возрастает, достигает максимума при оптимальной плотности, а затем резко снижается. v = v_{max}(1 - \frac{k}{k_{max}}), где v — средняя скорость, v_{max} — максимальная скорость, k — плотность потока, а k_{max} — максимальная плотность. Данная зависимость объясняет, почему увеличение числа автомобилей на дороге не всегда приводит к увеличению пропускной способности, а напротив, может вызывать образование заторов и снижение эффективности транспортной системы. Понимание этой взаимосвязи необходимо для разработки эффективных стратегий управления трафиком и оптимизации транспортных потоков.
Начальные условия, в частности, начальная плотность транспортного потока, оказывают определяющее влияние на последующую динамику пробок и их распространение. Исследования показывают, что даже незначительные колебания начальной плотности могут привести к существенным различиям в формировании заторов, продолжительности их существования и общей пропускной способности дорожной сети. k_0 — обозначение начальной плотности — служит отправной точкой для моделирования, позволяя прогнозировать развитие ситуации и оценивать эффективность различных стратегий управления трафиком. Недостаточная начальная плотность может привести к образованию «волн» низкой плотности, в то время как избыточная — к быстрому возникновению и усилению пробок, что подчеркивает критическую важность точного определения и учета этого параметра при построении адекватных моделей транспортного потока.
От Макро к Микро: Подходы к Моделированию Транспортных Потоков
Традиционные макроскопические модели транспортного потока используют законы сохранения для описания движения транспорта как сплошной среды. В основе лежит представление о трафике как о жидкости или газе, где плотность, скорость и расход описывают общее поведение потока. Эти модели оперируют средними значениями параметров, такими как средняя скорость и плотность транспортных средств на определенном участке дороги, упрощая сложные взаимодействия между отдельными транспортными средствами. Основными уравнениями, используемыми в этих моделях, являются уравнения непрерывности и импульса, адаптированные для описания потока транспорта. Применение законов сохранения позволяет анализировать и прогнозировать возникновение заторов и оценивать пропускную способность дорог, но не учитывает индивидуальные характеристики и поведение каждого транспортного средства.
Микроскопическое моделирование транспортных потоков представляет собой подход, в котором каждый автомобиль рассматривается как отдельный агент, обладающий собственными характеристиками (скорость, ускорение, габариты) и подчиняющийся определенным правилам поведения. В отличие от макроскопических моделей, описывающих трафик как сплошную среду, микроскопические модели позволяют детально воспроизводить взаимодействие между отдельными транспортными средствами, включая обгоны, перестроения и реакции на изменения дорожной обстановки. Несмотря на повышенную реалистичность, микроскопическое моделирование требует значительно больших вычислительных ресурсов, поскольку необходимо отслеживать состояние и перемещение каждого отдельного автомобиля в симуляции, что делает его более трудоемким и затратным по времени.
Для верификации предсказаний и точной настройки параметров как макроскопических, так и микроскопических моделей транспортных потоков используются данные, собираемые с зондирующих транспортных средств (probe vehicles). Эти данные включают информацию о местоположении, скорости и времени в пути отдельных автомобилей, что позволяет сравнивать результаты моделирования с реальными условиями на дорогах. Анализ расхождений между смоделированными и фактическими данными позволяет калибровать параметры моделей, такие как максимальная плотность потока, скорость насыщения и время реакции водителей, повышая их точность и надежность. Использование данных с зондирующих транспортных средств является критически важным для обеспечения соответствия моделей реальным транспортным условиям и улучшения качества прогнозирования.
Реконструкция Плотности Транспортного Потока: Основанный на Данных Подход
Основой реконструкции плотности транспортного потока является разработанная ‘Оптимизационная задача’, представляющая собой математическую модель для оценки распределения ‘Конечной плотности’ на основе разреженных измерений. Данная задача позволяет получить детальную картину плотности трафика, используя ограниченный набор данных, поступающих от различных источников. Модель формулируется как задача оптимизации, минимизирующая расхождение между предсказанным и наблюдаемым распределением плотности, при этом учитываются ограничения, связанные с физической природой транспортного потока. Решение данной задачи позволяет эффективно восстанавливать плотность трафика в областях, где прямые измерения отсутствуют или недостаточны.
Восстановление плотности транспортного потока демонстрирует точность, оцениваемую с помощью среднеквадратичной ошибки (MSE). При использовании набора данных, содержащего N=2000 измерений и временном интервале T=0.1, значение MSE составило 0.0483. Увеличение количества измерений до N=4000 и увеличение временного интервала до T=0.2 позволило снизить MSE до 0.0076. Эти результаты указывают на повышение точности реконструкции плотности транспортного потока при увеличении объема данных и продолжительности наблюдения.
Модель использует данные, полученные от зондирующих транспортных средств (Probe Vehicles), для восстановления полной картины транспортного потока, компенсируя пробелы в измерениях. При использовании N=2000 зондирующих автомобилей и времени T=0.1, относительная ошибка (RE) составляет 0.0053. Увеличение количества зондирующих автомобилей до N=4000 и времени до T=0.2 позволило снизить относительную ошибку до 0.0020, что свидетельствует о повышении точности реконструкции плотности транспортного потока при увеличении объема входных данных.
Проверка Точности Модели: Измерение Сходимости
Расстояние Вассерштейна представляет собой мощный математический инструмент, позволяющий количественно оценить разницу между вероятностными распределениями. В контексте реконструкции “Конечной Плотности” — вероятностного описания распределения транспортного потока — это расстояние служит ключевым показателем сходимости модели. По сути, оно измеряет минимальную “стоимость” перемещения одной вероятностной массы в другую, обеспечивая более надежную и интуитивно понятную метрику, чем традиционные методы, такие как евклидово расстояние. Применение расстояния Вассерштейна позволяет с высокой точностью определить, насколько хорошо реконструированная плотность соответствует исходным данным, и, следовательно, подтвердить адекватность и надежность разработанной модели для прогнозирования и управления транспортными потоками. W(P,Q) = \in f_{γ ∈ Π(P,Q)} E_{(x,y) \sim γ} [||x - y||], где Π(P,Q) — множество всех совместных распределений, имеющих P и Q в качестве маргинальных распределений.
Внезапные возмущения в транспортном потоке, проявляющиеся в виде так называемых “ударных волн”, могут быть точно зафиксированы и спрогнозированы с помощью тщательно валидированной модели. Данное явление, характеризующееся резким изменением плотности и скорости транспортных средств, часто приводит к образованию пробок и снижению пропускной способности дорог. Разработанная модель, благодаря использованию передовых алгоритмов и точным данным, способна не только регистрировать формирование этих волн, но и предсказывать их распространение, позволяя оперативно реагировать на потенциальные заторы и оптимизировать дорожный трафик. Точное моделирование таких сценариев имеет критическое значение для повышения безопасности дорожного движения и снижения негативных последствий, связанных с внезапными изменениями в транспортном потоке.
Достигнутая точность модели, подтвержденная значениями среднеквадратичной ошибки MSE = 0.0483 и 0.0076, а также относительной ошибки RE = 0.0053 и 0.0020, позволяет значительно улучшить стратегии управления транспортными потоками. Уменьшение погрешности в прогнозировании позволяет оперативно реагировать на изменения дорожной обстановки, минимизируя заторы и повышая пропускную способность магистралей. В конечном итоге, повышение точности модели напрямую способствует повышению безопасности всех участников дорожного движения, снижая вероятность возникновения аварийных ситуаций и обеспечивая более предсказуемые условия на дороге.
Представленное исследование демонстрирует изящный подход к реконструкции плотности транспортного потока, опираясь на сходимость макро- и микроскопических моделей. Подобно тому, как в математике стремление к пределу позволяет выявить фундаментальные константы, так и здесь, анализ транспортного потока при ограниченных данных позволяет приблизить оценку плотности к истинному значению. Как однажды заметил Исаак Ньютон: «Если я вижу дальше других, то это потому, что стою на плечах гигантов». В данном контексте, «гигантами» выступают как классические модели транспортного потока, так и современные методы машинного обучения, объединенные общей целью — точным описанием динамики транспортных потоков. Пусть N стремится к бесконечности — что останется устойчивым? В данном случае, устойчивым остаётся фундаментальный принцип сохранения плотности, даже при использовании приближенных методов реконструкции.
Куда Далее?
Представленная работа, безусловно, демонстрирует элегантность подхода к реконструкции плотности транспортного потока. Однако, следует признать, что обход явного обеспечения законов сохранения — это, скорее, прагматичное решение, нежели фундаментальное. Истинно корректное решение должно быть детерминированным; если реконструкция плотности не может быть воспроизведена с абсолютной точностью, ее достоверность вызывает сомнения. Необходимо сосредоточиться на интеграции принципов сохранения непосредственно в архитектуру нейронных сетей, а не полагаться на эмпирическую сходимость.
Особый интерес представляет вопрос о масштабируемости предложенного подхода. Успешная реконструкция плотности на ограниченном наборе данных — это лишь первый шаг. Более сложная задача — это работа с реальными транспортными потоками, характеризующимися высокой степенью нелинейности и непредсказуемости. Необходимо исследовать, насколько хорошо данный подход адаптируется к изменениям в структуре дорожной сети и к появлению новых видов транспортных средств.
В конечном итоге, задача реконструкции транспортного потока — это не просто техническая проблема, но и философский вызов. Попытка предсказать будущее на основе ограниченных данных — это всегда акт веры. Истинная элегантность заключается не в достижении высокой точности, а в осознании границ применимости любой модели. Следующим шагом должно стать исследование устойчивости предложенного подхода к шумам и ошибкам в исходных данных.
Оригинал статьи: https://arxiv.org/pdf/2602.11336.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- SOL ПРОГНОЗ. SOL криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- HYPE ПРОГНОЗ. HYPE криптовалюта
- SUI ПРОГНОЗ. SUI криптовалюта
- FARTCOIN ПРОГНОЗ. FARTCOIN криптовалюта
2026-02-14 06:41