Автор: Денис Аветисян
Обзор посвящен применению принципов римановой геометрии для создания более эффективных и устойчивых моделей обучения представлений графов.
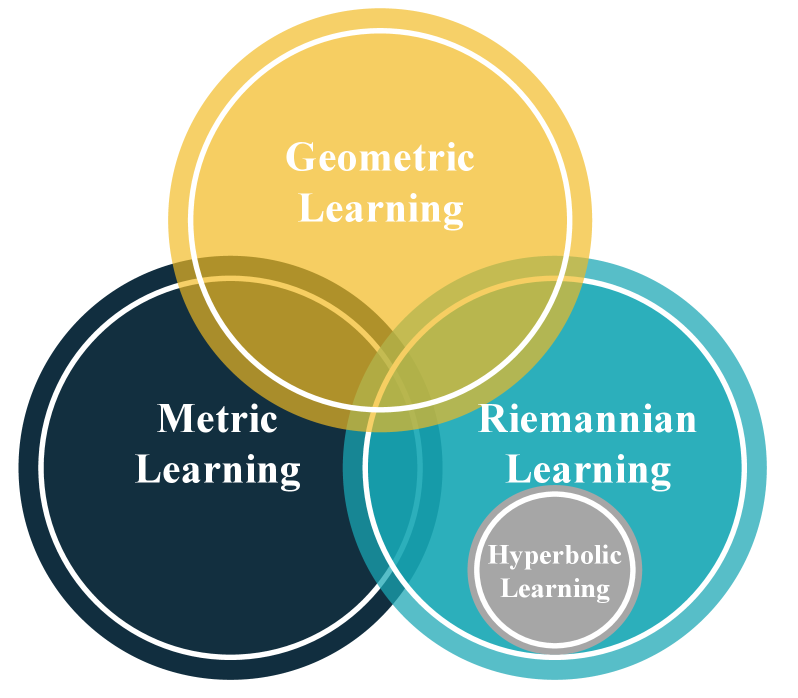
В статье представлен всесторонний анализ риманового обучения графов, включая теоретические основы, архитектурные подходы, парадигмы обучения и перспективные направления исследований.
Неевклидова природа графов представляет собой серьезную проблему для традиционных методов машинного обучения. В данной работе, ‘RiemannGL: Riemannian Geometry Changes Graph Deep Learning’, утверждается, что риманова геометрия является принципиальной основой для обучения представлений графов, объединяя разрозненные подходы в единую парадигму. Предлагается систематический обзор ключевых концепций, архитектур и парадигм обучения, демонстрирующий потенциал использования геометрических принципов для создания более выразительных и устойчивых моделей графов. Сможем ли мы раскрыть весь потенциал римановой геометрии для создания фундаментальных моделей обучения на графах нового поколения?
Пределы Евклидова Пространства: Когда Традиционные Графовые Методы Оказываются Недостаточными
Традиционные методы анализа графов часто опираются на евклидовы вложения, представляющие узлы и связи в виде точек на плоскости или в пространстве. Однако, многие реальные сети, такие как социальные сети, биологические сети или сети знаний, обладают сложными, нелинейными взаимосвязями, которые трудно адекватно отобразить в этих плоских представлениях. Попытки свести сложные структуры к евклидовой геометрии приводят к потере информации о реальных отношениях между элементами сети, что особенно заметно при анализе данных высокой размерности или при наличии скрытых зависимостей. В результате, эффективность алгоритмов, основанных на евклидовых вложениях, снижается, и возникают сложности с интерпретацией полученных результатов, поскольку плоское представление искажает истинную структуру сети и упускает важные нюансы.
Ограничения, возникающие при использовании традиционных методов анализа графов, особенно заметны в задачах, требующих глубокого понимания геометрической структуры данных. Например, в системах обнаружения аномалий, где выявление отклонений от нормального поведения критически зависит от точного определения расстояний и связей между объектами, упрощенные представления могут приводить к ложным срабатываниям или, наоборот, к пропуску реальных угроз. Аналогичная проблема возникает и в рекомендательных системах: если связи между пользователями и предметами не отражают истинную сложность их взаимоотношений, рекомендации становятся нерелевантными и неэффективными. Неспособность уловить нюансы геометрической организации данных снижает точность предсказаний и ухудшает качество предоставляемых услуг, что подчеркивает необходимость разработки более совершенных методов анализа, способных эффективно работать с неевклидовыми пространствами и сложными сетевыми структурами.
Представление данных в плоском пространстве неизбежно приводит к потере важной информации об их взаимосвязях. Традиционные методы анализа графов, оперирующие с евклидовыми вложениями, часто упрощают сложные, нелинейные отношения, присущие реальным сетям. Это упрощение не только снижает точность решения задач, таких как выявление аномалий или построение рекомендательных систем, но и затрудняет интерпретацию результатов. Потеря информации о структуре связей приводит к тому, что алгоритмы не способны уловить тонкие нюансы в данных, что выражается в ухудшении производительности и снижении способности извлекать полезные знания. В конечном итоге, подобный подход ограничивает возможности глубокого анализа и понимания сложных сетевых структур.
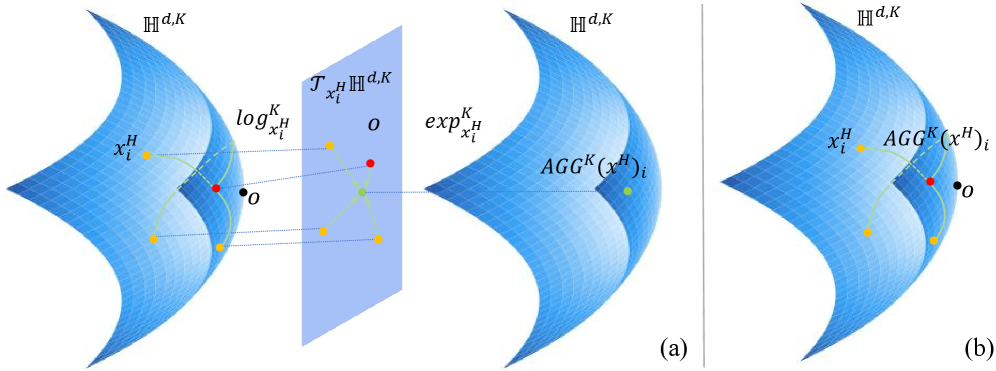
Риманова Геометрия для Обучения Графов: Новый Фундамент
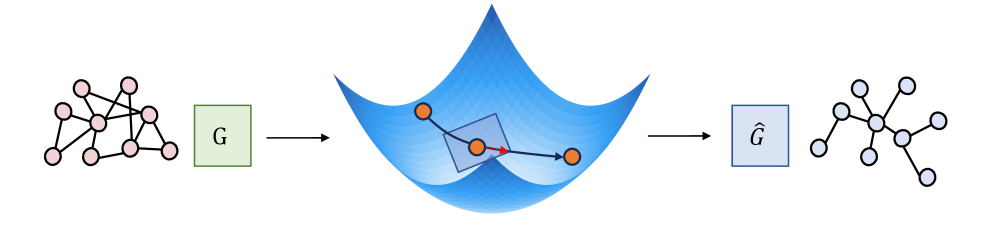
Римановы многообразия представляют собой мощный математический аппарат для анализа и представления данных, структурированных в виде графов. В отличие от традиционных евклидовых пространств, римановы многообразия позволяют учитывать внутреннюю геометрию графа, определяемую связями между узлами и их свойствами. Это достигается путем определения RiemannianMetric — функции, которая задает понятие длины кривых на многообразии и позволяет измерять расстояния между точками, представляющими узлы графа. Использование римановых многообразий позволяет создавать более выразительные и точные представления графовых данных, сохраняя информацию о структуре, которая может быть потеряна при использовании евклидовых вложений. Примерами таких пространств являются гиперболическое пространство, сферическое пространство и многообразие Грассмана, каждое из которых подходит для анализа графов с различными характеристиками и свойствами.
Различные типы римановых многообразий предоставляют инструменты для определения подходящей геометрии в зависимости от типа данных, представленных графом. RiemannianMetric определяет способ измерения расстояний на многообразии, позволяя учитывать внутреннюю структуру данных. HyperbolicSpace эффективно моделирует иерархические данные и графы с экспоненциальным ростом, в то время как SphericalSpace подходит для данных, требующих представления на ограниченной области. GrassmannManifold используется для представления подпространств векторных пространств, что полезно для анализа данных, характеризующихся набором признаков или векторов.
Использование римановых многообразий позволяет алгоритмам сохранять критически важную структурную информацию, теряемую при евклидовых вложениях. Традиционные методы встраивания графов в евклидово пространство приводят к искажению геометрии данных, особенно в случаях, когда узлы и ребра представляют собой нелинейные отношения. В отличие от этого, представление графа на римановом многообразии, таком как \mathbb{H}^n (гиперболическое пространство) или \mathbb{S}^n (сфера), позволяет сохранить естественные расстояния и отношения между узлами. Это, в свою очередь, повышает точность задач анализа графов, включая классификацию узлов, предсказание связей и кластеризацию, поскольку алгоритмы оперируют с более точным и полным представлением данных. Сохранение геометрии особенно важно для графов со сложной структурой, таких как социальные сети и сети знаний.
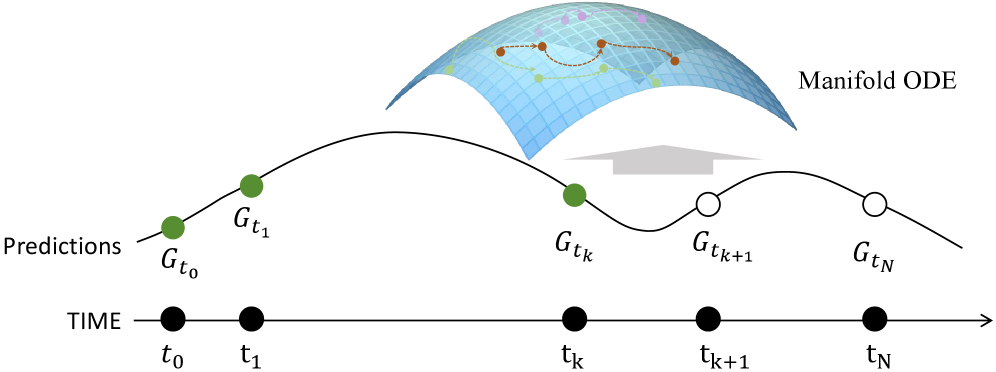
Методы Обучения на Римановых Графах: От VAE до ODE
Методы, такие как RiemannianVAE, RiemannianGCN и RiemannianODE, представляют собой адаптацию существующих архитектур глубокого обучения к римановому пространству. В отличие от традиционных методов, работающих с евклидовыми пространствами, эти подходы используют геометрию римановых многообразий для более эффективного представления графов. Это достигается за счет использования римановой метрики для определения расстояний и кривизны, что позволяет учитывать неевклидову структуру данных. Адаптация включает в себя замену стандартных операций, таких как свертки и градиентные спуски, на их аналоги, определенные для римановых многообразий, что обеспечивает более точное моделирование сложных взаимосвязей в графах и улучшает производительность в задачах обучения представлений.
Метод RiemannianSDE представляет собой вероятностный подход к генерации и анализу графов, обладающих сложными геометрическими свойствами. В основе лежит использование стохастических дифференциальных уравнений (SDE) на римановых многообразиях, что позволяет моделировать эволюцию графа как случайный процесс. Такой подход позволяет учитывать геометрическую структуру данных при генерации новых графов или анализе существующих, что особенно полезно для задач, где важны не только топологические, но и метрические свойства графа. RiemannianSDE позволяет оценивать вероятностные распределения над графами и использовать их для задач генерации, реконструкции и анализа структурных особенностей графов.
Применение методов, основанных на римановых многообразиях, позволяет улучшить результаты в задачах классификации узлов, предсказания связей и генерации графов за счет использования геометрических свойств данных. В частности, риманова геометрия предоставляет инструменты для анализа кривизны и геодезических расстояний между узлами, что позволяет более точно моделировать взаимосвязи в графе. Использование римановых метрик позволяет учитывать неевклидову структуру данных, что особенно важно для графов, представляющих сложные системы с нелинейными зависимостями. Улучшение производительности достигается за счет более эффективного представления данных и более точного учета геометрических свойств графа, что приводит к повышению точности и надежности результатов в задачах машинного обучения на графах.
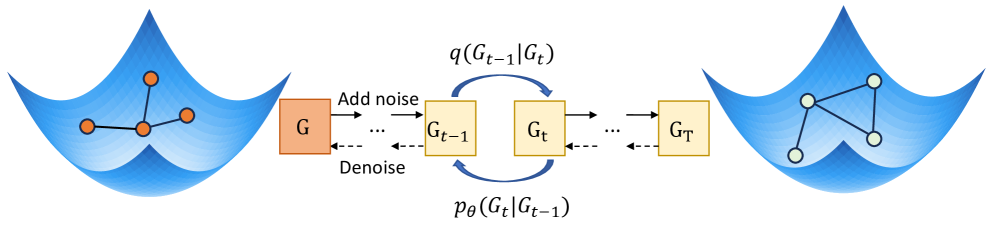
Неконтролируемое Обучение и Перенос Знаний: Расширяя Возможности Римановых Графов
Сочетание римановой геометрии с методами неконтролируемого и полуконтролируемого обучения открывает новые возможности для анализа графовых данных, не требующих предварительной разметки. В отличие от традиционных подходов, рассматривающих графы как дискретные структуры, риманова геометрия позволяет определить непрерывную структуру на графе, учитывая взаимосвязи между узлами и их атрибутами. Это позволяет алгоритмам неконтролируемого обучения, таким как кластеризация и понижение размерности, более эффективно выявлять скрытые закономерности и структуры в данных. Например, Риманова спектральная кластеризация, использующая риманову геометрию для определения расстояний между узлами, демонстрирует превосходство над традиционными методами в задачах анализа социальных сетей и биологических данных. Применение полуконтролируемого обучения, в свою очередь, позволяет использовать небольшое количество размеченных данных для улучшения качества обучения и обобщающей способности модели, что особенно актуально в условиях ограниченных ресурсов.
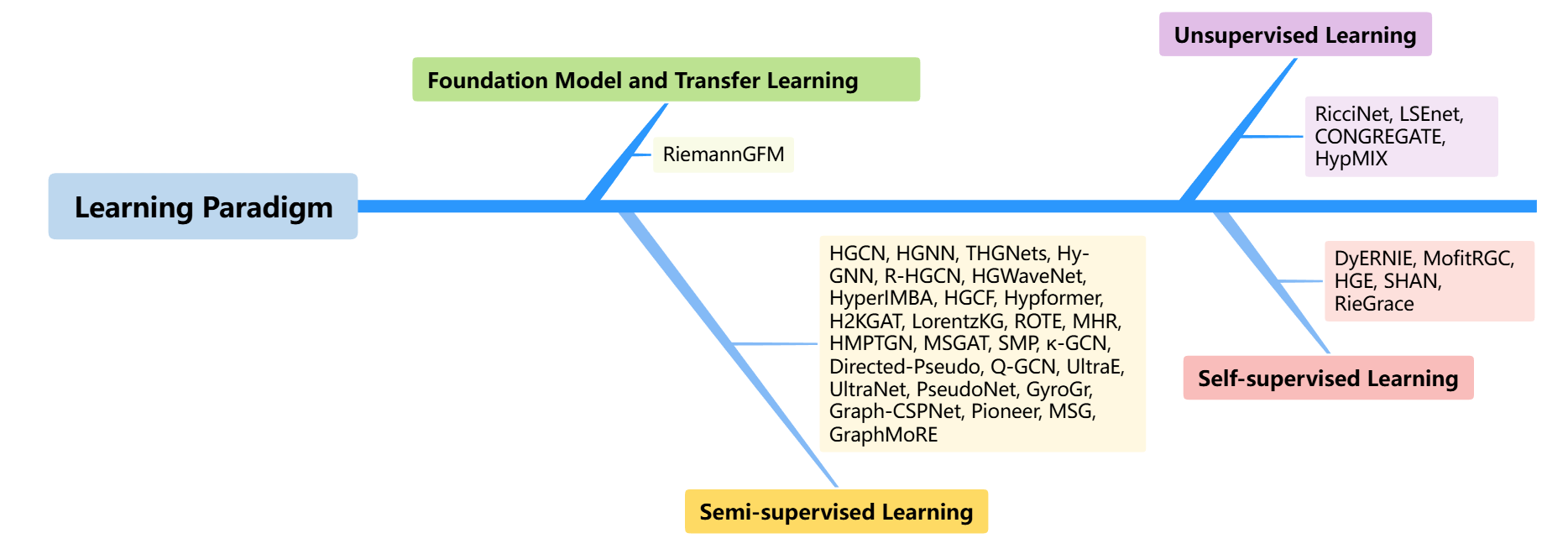
В настоящее время активно развивается подход к обучению, основанный на переносе знаний [TransferLearning], позволяющий использовать предварительно обученные модели на масштабных графах для создания так называемых «фундаментальных моделей графов» [GraphFoundationModel]. Эти модели, обученные на обширных данных, способны эффективно адаптироваться к новым задачам и графам, даже при ограниченном количестве размеченных данных. Такой перенос знаний значительно ускоряет процесс обучения и повышает обобщающую способность моделей, особенно в сценариях, где сбор и разметка данных являются дорогостоящими или трудоемкими. В результате, предварительно обученные модели становятся ценным ресурсом для решения широкого спектра задач, связанных с анализом и обработкой графовых данных, от рекомендательных систем до прогнозирования связей в социальных сетях.
Методы встраивания графов знаний, такие как KnowledgeGraphEmbedding, значительно выигрывают от использования более богатых геометрических представлений данных. Вместо традиционных векторных представлений, основанных на дискретных отношениях, геометрический подход позволяет кодировать информацию о структуре графа и взаимосвязях между сущностями в виде кривизны и расстояний на римановом многообразии. Это не только повышает точность предсказаний и улучшает производительность алгоритмов, но и делает полученные представления более интерпретируемыми. Анализ геометрических свойств графа позволяет выявлять скрытые закономерности и взаимосвязи, которые остаются незамеченными при использовании традиционных методов, что открывает новые возможности для анализа и понимания сложных систем знаний.
Будущие Направления: К Геометрическому Глубокому Обучению для Сложных Систем
Расширение возможностей обучения на римановых графах до более сложных многообразий, таких как псевдоримановы и произведения многообразий, открывает новые перспективы для моделирования чрезвычайно сложных взаимосвязей в данных. Традиционные методы анализа графов часто не способны адекватно отразить нюансы, присущие данным, представленным на этих многообразиях. В отличие от них, использование псевдоримановой геометрии позволяет учитывать неевклидовы метрики, что критически важно для анализа данных, где понятия расстояния и направления могут быть нетрадиционными. Аналогично, использование произведений многообразий позволяет эффективно представлять и анализировать данные, имеющие иерархическую или композитную структуру. Это расширение геометрического подхода позволяет не только более точно моделировать сложные системы, но и извлекать из них более глубокие и значимые знания, что потенциально может привести к прорывам в различных областях науки и техники.
Интеграция методов обработки сигналов на графах (GraphSignalProcessing) с римановой геометрией открывает новые возможности для углубленного анализа и извлечения признаков из сложных графовых структур. Традиционные методы анализа графов часто игнорируют внутреннюю геометрию данных, рассматривая узлы и связи как дискретные элементы. Однако, применение GSP позволяет рассматривать сигналы, определенные на графе, как непрерывные функции, что позволяет использовать инструменты дифференциальной геометрии для их анализа. Это особенно важно при работе с данными, имеющими естественную геометрическую структуру, такими как сети социальных взаимодействий или молекулярные структуры. Благодаря возможности определения градиентов, лапласианов и других геометрических операторов непосредственно на графе, становится возможным эффективное выделение ключевых признаков и выявление скрытых закономерностей, недоступных при использовании стандартных подходов. В результате, интеграция GSP и римановой геометрии значительно расширяет возможности анализа графов, позволяя решать задачи, требующие учета сложной геометрии данных.
Перспективная парадигма геометрического глубокого обучения обещает кардинальные изменения в различных областях науки и техники. В анализе социальных сетей данный подход позволит выявлять сложные взаимосвязи и паттерны взаимодействия, недоступные традиционным методам. В сфере разработки лекарств, геометрическое моделирование молекулярных структур и их взаимодействий с биологическими мишенями может значительно ускорить процесс открытия новых препаратов. Кроме того, в материаловедении, анализ геометрических свойств материалов на микро- и нано-уровне открывает возможности для создания материалов с заданными характеристиками и уникальными свойствами. Развитие данной области исследований предполагает появление принципиально новых инструментов для анализа и моделирования сложных систем, что может привести к прорывным открытиям и инновациям в ближайшем будущем.
Исследование, представленное в данной работе, демонстрирует стремление к элегантности в сложном мире графовых нейронных сетей. Авторы показывают, как применение принципов римановой геометрии позволяет создать более выразительные и устойчивые представления графов. Это напоминает слова Андрея Николаевича Колмогорова: «Математика — это искусство не делать ничего лишнего». Действительно, в основе успешного моделирования лежит не усложнение архитектуры, а извлечение существенной информации и отказ от избыточности. Особое внимание к кривизне пространства, как ключевому элементу римановой геометрии, подтверждает эту тенденцию к лаконичности и точности в представлении данных.
Куда же дальше?
Представленный обзор, стремясь к ясности в сложном ландшафте геометрического обучения графам, неизбежно обнажил не столько ответы, сколько зияющие прорехи. Попытки вместить всю сложность графа в рамки римановых многообразий, хотя и плодотворны, пока остаются упрощением. Истинная геометрия данных, вероятно, гораздо более искривлена и многогранна, чем позволяет текущий математический аппарат. Следующим шагом видится отказ от навязчивой идеи об универсальном римановом пространстве, замена ее динамическими, адаптирующимися геометрическими моделями.
Особую тревогу вызывает зависимость от вычисления кривизны. Это — дорогостоящая операция, и ее интерпретация зачастую туманна. Необходимо искать инварианты, которые отражают геометрические свойства графа, не требуя явного вычисления кривизны. Интуиция подсказывает, что существуют более элегантные способы понять геометрию графа, основанные на принципах топологии и теории категорий. Простота — вот высшая форма сложности.
В конечном итоге, успех этого направления зависит от способности отойти от метафоры “пространства” как таковой. Граф — это не просто набор точек в пространстве, это — отношение между ними. Истинное понимание графа требует отказа от геометрических аналогий и сосредоточения на алгебраических и логических структурах, лежащих в его основе. Тогда, возможно, удастся построить модели, которые будут не просто “учиться” на графах, но и понимать их.
Оригинал статьи: https://arxiv.org/pdf/2602.10982.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- SOL ПРОГНОЗ. SOL криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- SUI ПРОГНОЗ. SUI криптовалюта
- HYPE ПРОГНОЗ. HYPE криптовалюта
- FARTCOIN ПРОГНОЗ. FARTCOIN криптовалюта
2026-02-12 20:44