Автор: Денис Аветисян
Исследователи представили AutoSpec — нейросеть, способную самостоятельно разрабатывать эффективные итерационные алгоритмы для численных задач линейной алгебры.
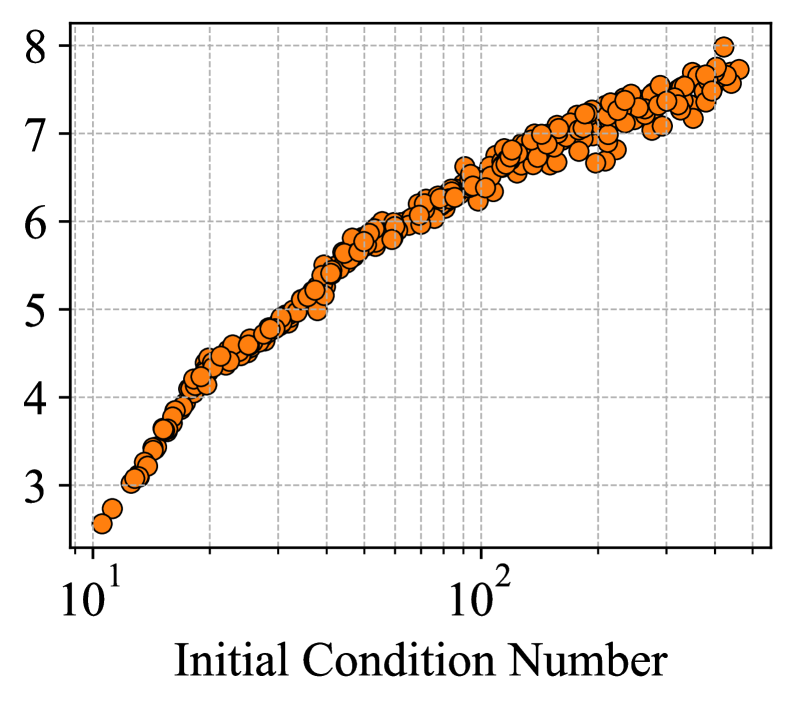
AutoSpec адаптируется к спектральным свойствам операторов для поиска оптимальных методов итеративного решения.
Эффективная разработка и оптимизация итерационных алгоритмов для крупномасштабных задач линейной алгебры и оптимизации традиционно требует значительных экспертных знаний. В данной работе, ‘Learning to Discover Iterative Spectral Algorithms’, представлена AutoSpec — нейросетевая платформа, способная самостоятельно находить и реализовывать эффективные итерационные алгоритмы, адаптируясь к спектральным характеристикам входных операторов. Ключевым достижением является обучение модели предсказывать коэффициенты рекуррентных соотношений для вычисления или применения матричного полинома, ориентированного на конкретную задачу. Сможет ли AutoSpec автоматизировать процесс разработки высокопроизводительных численных методов и открыть новые горизонты в решении сложных вычислительных задач?
Разоблачение Вычислительных Преград: Ключ к Эффективности
Решение больших систем линейных уравнений является краеугольным камнем множества научных и инженерных задач, от моделирования климата и анализа структур до машинного обучения и обработки изображений. Однако, традиционные итерационные методы, такие как метод Гаусса-Зейделя или метод сопряженных градиентов, часто сталкиваются с трудностями при работе с системами, насчитывающими миллионы или даже миллиарды неизвестных. Проблемы производительности и масштабируемости возникают из-за экспоненциального роста вычислительных затрат и требований к памяти по мере увеличения размера системы Ax = b. Эти методы могут требовать значительного времени для сходимости, особенно для плохо обусловленных матриц, что ограничивает их применимость в задачах, требующих оперативных результатов и обработки больших объемов данных.
Традиционные итеративные методы решения систем линейных уравнений часто требуют тщательной настройки параметров и применения стратегий предварительной обработки, что значительно усложняет процесс оптимизации. Эффективность этих методов напрямую зависит от экспертных знаний и опыта специалиста, способного подобрать оптимальные значения параметров для конкретной задачи. Подбор этих параметров — трудоемкий и ресурсозатратный процесс, требующий проведения многочисленных экспериментов и анализа результатов. Более того, оптимальные параметры, найденные для одной задачи, могут оказаться неэффективными для другой, что подчеркивает необходимость разработки более автоматизированных и адаптивных подходов, способных минимизировать зависимость от ручной настройки и снизить общие вычислительные затраты. Отсутствие универсальных стратегий предварительной обработки представляет собой серьезное препятствие для широкого применения этих методов в задачах, требующих высокой производительности и масштабируемости, особенно при работе с большими объемами данных и сложными моделями.
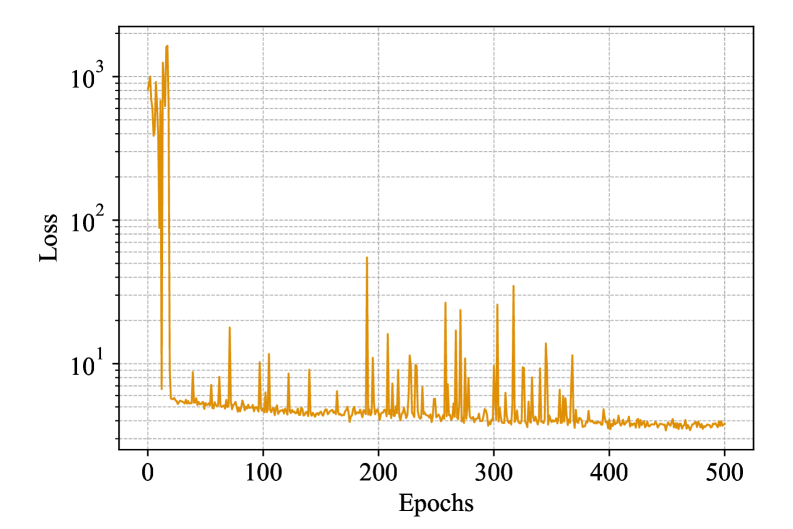
AutoSpec: Алгоритмическое Открытие Через Глубокое Обучение
AutoSpec представляет собой новый подход к разработке итерационных спектральных методов, основанный на использовании глубокого обучения. В отличие от традиционных методов, требующих ручного проектирования и настройки алгоритмов, AutoSpec позволяет автоматически обнаружить оптимальные схемы итераций. Это достигается путем обучения нейронной сети, способной генерировать эффективные алгоритмы на основе анализа характеристик решаемой задачи, что значительно сокращает время и усилия, необходимые для разработки высокопроизводительных численных методов. Автоматическое обнаружение алгоритмов позволяет применять данный подход к широкому классу задач, для которых ручная разработка алгоритмов представляется сложной или невозможной.
В основе AutoSpec лежит нейросетевой движок, который обучается построению итерационных алгоритмов на основе спектральных проб — приближенных собственных значений и норм остатков. Эти спектральные пробы служат для характеризации структуры решаемой задачи, позволяя движку выявлять ключевые свойства, такие как спектральный радиус и распределение собственных значений. Нейронная сеть анализирует полученные данные и на их основе формирует операторы, определяющие итерационную схему. Таким образом, движок способен автоматически синтезировать алгоритмы, адаптированные к конкретным характеристикам задачи, без необходимости ручного проектирования и настройки.
В основе механизма AutoSpec лежит использование операторных полиномов для построения эффективных итерационных схем. Данный подход позволяет представлять линейный оператор A в виде полиномиальной функции от оператора B, где B является более простым в реализации и вычислении. Итерационные схемы, основанные на операторных полиномах, конструируются таким образом, чтобы минимизировать остаток ||x - Ax|| на каждой итерации, приближая решение к собственному вектору оператора A. Выбор конкретного операторного полинома и его параметров осуществляется нейронной сетью, обученной на анализе спектральных проб, что позволяет автоматически адаптировать алгоритм к структуре решаемой задачи и достигать высокой скорости сходимости.
![AutoSpec - это система, использующая обученную нейронную сеть и рекуррентную формулу для определения численных алгоритмов, позволяющих извлекать спектральную информацию (<span class="katex-eq" data-katex-display="false">\widehat{\bm{\lambda}},\widehat{\bm{r}}</span>) из оператора <span class="katex-eq" data-katex-display="false">𝐗</span>, параметризовать полином <span class="katex-eq" data-katex-display="false">P(\cdot)[latex] и осуществлять самообучение на основе градиента потерь, вычисляемых для конечного состояния [latex]𝐕_{d+1}</span>.](https://arxiv.org/html/2602.09530v1/x2.png)
Использование Спектральных Свойств для Повышения Эффективности
AutoSpec использует информацию об эйгенспектре матриц для определения оптимальных итерационных стратегий. Анализ эйгензначений и собственных векторов позволяет выявить доминирующие характеристики решаемой задачи, такие как обусловленность и спектральный радиус. На основе этих данных AutoSpec конструирует итерационные методы, адаптированные к конкретным свойствам матрицы, например, выбирает подходящие предварительные решатели или схемы сходимости. Такой подход позволяет значительно повысить эффективность и скорость сходимости численных алгоритмов по сравнению с универсальными методами, не учитывающими особенности решаемой задачи. В частности, AutoSpec может автоматически настраивать параметры итерационных методов, чтобы минимизировать число итераций, необходимых для достижения заданной точности.
В основе AutoSpec лежит поддержка методов, не требующих явного хранения и вычислений с матрицами (Matrix-Free Methods). Вместо непосредственной работы с матричным представлением задачи, эти методы используют функциональные приближения и итеративные процедуры для оценки матрично-векторных произведений. Это позволяет значительно снизить требования к памяти и вычислительным ресурсам, особенно при работе с большими разреженными матрицами, что критически важно для задач высокой размерности и обеспечивает существенное повышение масштабируемости и эффективности алгоритмов. Отказ от явного хранения матрицы позволяет обрабатывать задачи, которые не помещаются в оперативную память, и снижает накладные расходы, связанные с операциями над большими матрицами.
В AutoSpec применяется метод минимаксовской аппроксимации, направленный на минимизацию максимальной ошибки решения. Этот подход, стимулирующий эквириппл-поведение (равномерные колебания ошибки), обеспечивает устойчивость и точность вычислений. Вместо стремления к минимизации среднеквадратичной ошибки, метод фокусируется на ограничении максимального отклонения, что критически важно для задач, где даже небольшие пиковые ошибки недопустимы. ||f - f_n||_{\in fty} = \min , где f - целевая функция, а f_n - её аппроксимация.
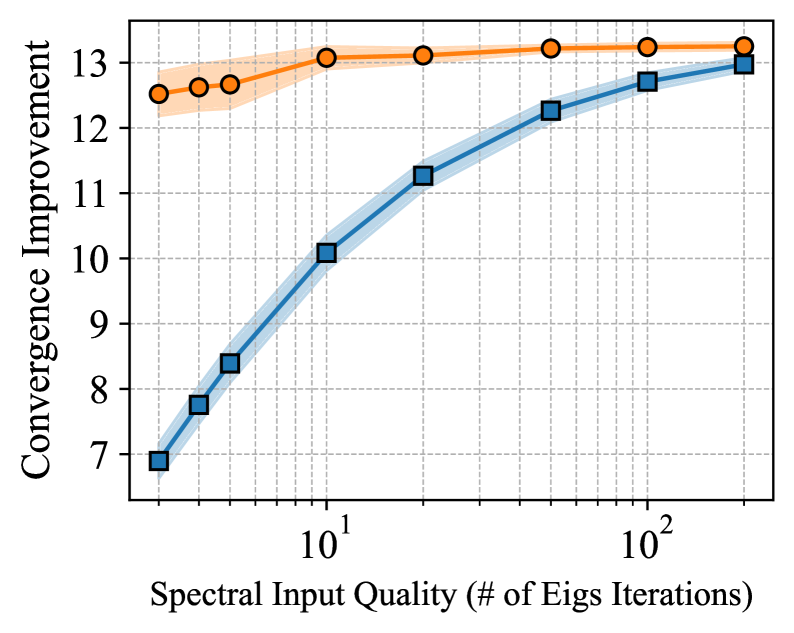
Расширение Горизонтов: За Пределами Традиционных Методов
Автоматизированная система AutoSpec продемонстрировала способность к самостоятельному «открытию» хорошо известных и эффективных алгоритмов, в частности, метода сопряжённых градиентов (Conjugate Gradient, CG). Этот факт является важным подтверждением работоспособности системы и её потенциала в области автоматического поиска оптимальных вычислительных стратегий. Успешное воссоздание CG, алгоритма, широко применяемого для решения систем линейных уравнений, указывает на то, что AutoSpec не просто генерирует случайные комбинации операций, но способна выявлять и воспроизводить принципы, лежащие в основе высокопроизводительных методов. Данный результат служит надёжной основой для дальнейших исследований и разработки более сложных алгоритмов, а также подтверждает эффективность подхода к автоматизированному поиску решений в различных областях вычислительной математики.
Исследования показали, что AutoSpec не только успешно воспроизводит известные алгоритмы, такие как Метод Сопряженных Градиентов, но и обнаруживает принципиально новые подходы к решению сложных задач. Эти инновационные методы демонстрируют значительное превосходство над традиционными алгоритмами в определенных сценариях, обеспечивая ускорение сходимости на несколько порядков величины. Такой существенный прирост эффективности открывает возможности для решения ранее недоступных задач, требующих высокой скорости вычислений и позволяя значительно сократить время, необходимое для получения результатов. Это указывает на огромный потенциал AutoSpec в качестве инструмента для автоматического поиска и оптимизации алгоритмов, способного значительно расширить границы вычислительных возможностей.
Автоматизация процесса разработки алгоритмов становится все более актуальной, и данная платформа предлагает перспективные пути для ее реализации. Используя методы обнаружения алгоритмов, такие как обучение с подкреплением (RL) и большие языковые модели (LLM), система способна не только находить существующие эффективные подходы, но и самостоятельно создавать новые, оптимизированные решения. Обучение с подкреплением позволяет системе экспериментировать с различными алгоритмическими стратегиями, вознаграждая наиболее успешные, а LLM способны генерировать и оценивать алгоритмический код, значительно ускоряя процесс поиска оптимальных решений. Такой симбиоз традиционных методов оптимизации и передовых технологий машинного обучения открывает возможности для создания самообучающихся алгоритмов, адаптирующихся к специфическим задачам и превосходящих существующие подходы по эффективности и скорости сходимости.
В рамках исследования поддерживается использование полиномиальной предварительной обработки, основанной на полиномах Чебышева, что позволяет оптимизировать обнаруженные алгоритмы. Этот подход направлен на минимизацию ошибки, приближая её к теоретическому минимуму - так называемой minimax-ошибке. Применение полиномов Чебышева обеспечивает эффективное масштабирование и улучшение обусловленности решаемых задач, что особенно важно при работе с большими объемами данных и сложными вычислительными моделями. Полученные результаты демонстрируют, что предложенная методика позволяет достигать ошибок, близких к оптимальным, что подтверждает высокую эффективность и практическую значимость разработанного подхода к оптимизации алгоритмов.
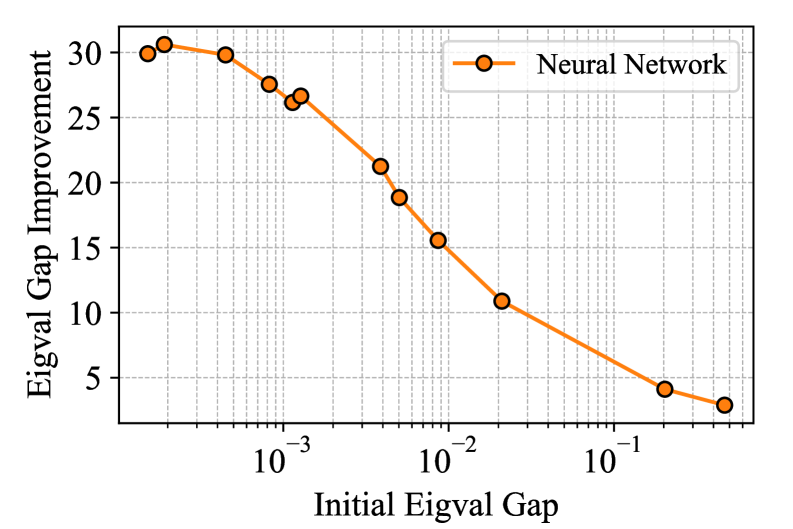
Исследование, представленное в данной работе, демонстрирует стремление к преодолению границ традиционных алгоритмов, подобно тому, как исследователь ищет закономерности в хаосе. Автоматизированный подход к обнаружению и реализации итеративных алгоритмов, основанный на адаптации к спектральным свойствам операторов, напоминает о важности понимания внутренней структуры системы для её оптимизации. Алан Тьюринг однажды заметил: «Иногда люди, которые кажутся сумасшедшими, просто видят мир в другом разрешении». В данном случае, AutoSpec, подобно новаторскому мышлению Тьюринга, позволяет взглянуть на задачу численного линейного алгебры под новым углом, открывая возможности для создания более эффективных и адаптируемых алгоритмов, чем те, что созданы вручную. Этот подход к автоматическому поиску оптимальных методов представляет собой реверс-инжиниринг самой математической логики.
Что дальше?
Представленная работа, демонстрируя способность AutoSpec к "самообучению" итеративным алгоритмам, неизбежно ставит вопрос о границах применимости подобных подходов. Если эффективность алгоритма определяется не "ручным" анализом, а адаптацией к спектральным свойствам оператора, то возникает закономерный интерес: насколько глубоко скрыты закономерности в "хаосе" линейной алгебры, которые способны "увидеть" нейронные сети, но упускают из виду аналитики?
Очевидным направлением исследований представляется расширение класса решаемых задач. AutoSpec, судя по всему, преуспевает там, где традиционные методы испытывают трудности. Однако, способны ли подобные системы "взломать" более сложные задачи, требующие не только численной оптимизации, но и принципиально новых подходов к предобуславливанию и построению итерационных схем? Поиск универсальных, "обучаемых" принципов предобуславливания представляется задачей, достойной внимания.
Нельзя исключать и обратную связь: анализ "внутренней логики" AutoSpec может привести к переосмыслению классических алгоритмов. Возможно, скрытые в "черном ящике" сети принципы позволят создать более эффективные и элегантные решения, основанные не на "слепой" оптимизации, а на глубоком понимании структуры решаемых задач. И, конечно, интересен вопрос о том, как подобные системы будут взаимодействовать с человеком - станут ли они инструментом для расширения аналитических возможностей, или же заменят собой человеческий разум в области численных методов.
Оригинал статьи: https://arxiv.org/pdf/2602.09530.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- SOL ПРОГНОЗ. SOL криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- SUI ПРОГНОЗ. SUI криптовалюта
- FARTCOIN ПРОГНОЗ. FARTCOIN криптовалюта
- HYPE ПРОГНОЗ. HYPE криптовалюта
2026-02-12 05:39