Автор: Денис Аветисян
Новая методика позволяет эффективно отсеивать зашумленные данные в процессе обучения моделей машинного обучения, используемых для моделирования молекулярной динамики.
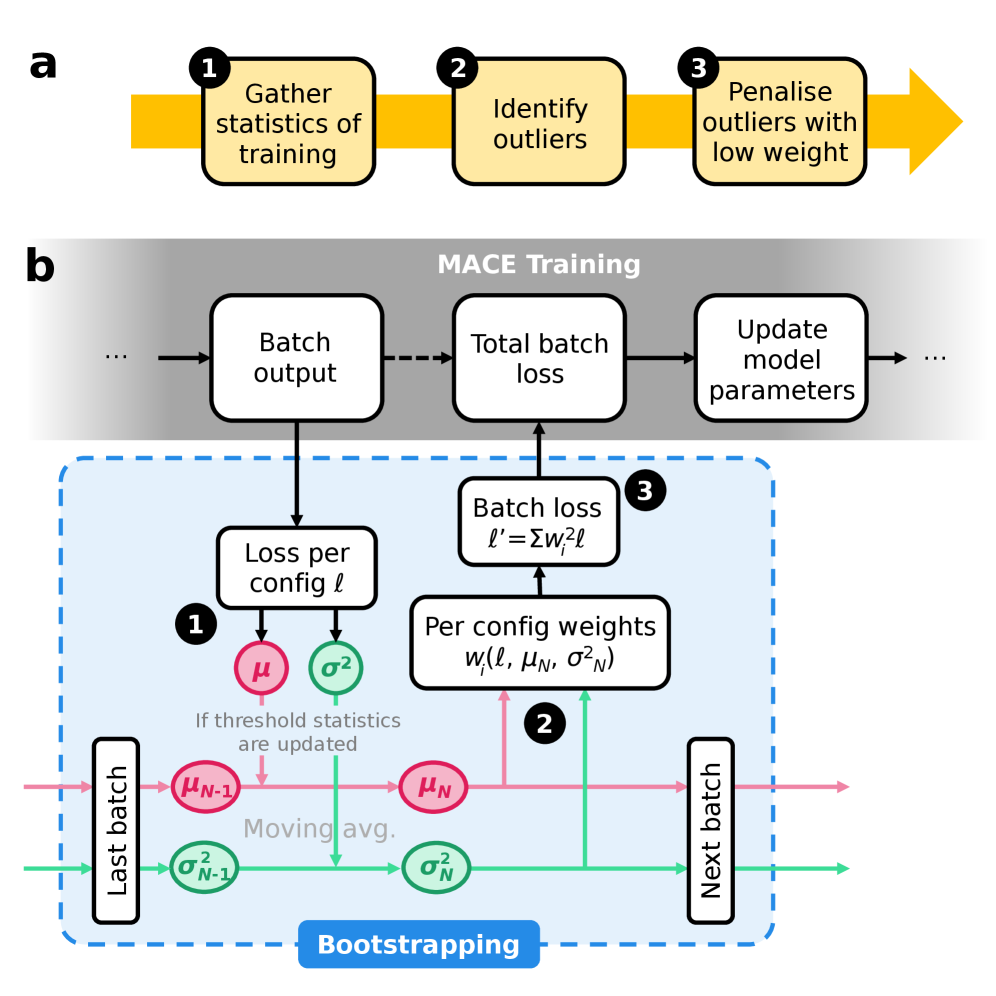
В статье представлен динамический метод бутстрэппинга для повышения устойчивости и точности обучения потенциалов межатомного взаимодействия, особенно при создании фундаментальных моделей.
Несмотря на прогресс в машинном обучении, точность межатомных потенциалов страдает от шума в исходных данных. В работе «Cutting Through the Noise: On-the-fly Outlier Detection for Robust Training of Machine Learning Interatomic Potentials» представлен автоматизированный метод выявления и подавления выбросов непосредственно в процессе обучения, не требующий дополнительных расчетов. Этот подход, основанный на отслеживании распределения потерь с помощью экспоненциального скользящего среднего, позволяет повысить точность и эффективность обучения, особенно при создании фундаментальных моделей. Сможет ли данная стратегия стать стандартным инструментом для обучения надежных моделей на неидеальных данных в молекулярной динамике и смежных областях?
Вызов Точности: Преодоление Ограничений Квантово-Химических Расчетов
Высокоточные расчеты электронной структуры, основанные на методах Ab Initio Quantum Chemistry, обеспечивают наиболее надежное описание поведения электронов в молекулах и материалах. Однако, сложность этих методов растет экспоненциально с увеличением числа электронов и атомов в системе, что делает их применение к сложным молекулам или большим системам чрезвычайно затратным в вычислительном плане. Например, для моделирования даже умеренно больших белков или наночастиц требуется огромное количество вычислительных ресурсов и времени, что ограничивает возможность проведения детальных исследований их свойств и реакционной способности. Вследствие этого, ученые постоянно ищут компромиссы между точностью и вычислительной эффективностью, разрабатывая новые алгоритмы и приближения, позволяющие моделировать более сложные системы без существенной потери качества расчетов.
Теория функционала плотности (ТФП), широко используемый метод в квантовой химии, обеспечивает значительное ускорение расчетов электронной структуры по сравнению с более точными, но ресурсоемкими подходами. Однако, несмотря на свою скорость, ТФП подвержена проблемам с точностью и сходимостью. Выбор подходящего функционала плотности может существенно влиять на результаты, а неточности в аппроксимации обменного-корреляционного функционала приводят к систематическим ошибкам. Кроме того, достижение сходимости в самосогласованных расчетах ТФП не всегда гарантировано, особенно для сложных молекулярных систем и требует тщательной настройки параметров расчета. Эти факторы могут существенно влиять на надежность полученных результатов и требуют критической оценки при интерпретации данных, полученных с использованием ТФП.
Стохастические методы, такие как вариационный метод Монте-Карло и диффузионный метод Монте-Карло, несмотря на свою способность решать сложные квантово-механические задачи, подвержены внутреннему шуму. Этот шум возникает из-за случайной природы используемых алгоритмов, где результаты вычислений определяются статистической выборкой. Вследствие этого, получаемые «точные» решения не являются абсолютно детерминированными, а содержат определенную степень неопределенности. Величина этого шума влияет на точность получаемых эталонных данных, используемых для проверки и калибровки других, менее точных, вычислительных методов. Оценка и минимизация этого статистического шума, например, путем увеличения числа статистических выборок или использования специальных алгоритмов снижения дисперсии, является критически важной задачей для обеспечения надежности и воспроизводимости результатов, получаемых с помощью этих мощных вычислительных инструментов. σ = \sqrt{Var(X)} — стандартное отклонение, являющееся мерой этого шума.
Машинное Обучение Межатомных Потенциалов: Путь к Вычислительной Эффективности
Потенциалы межатомного взаимодействия, основанные на машинном обучении (MLIP), представляют собой перспективный подход к ускорению молекулярно-динамических симуляций. Традиционно, точное моделирование сил между атомами требует вычислений Ab Initio, которые, несмотря на свою высокую точность, являются вычислительно затратными. MLIP обучаются на данных, полученных в результате этих дорогостоящих Ab Initio расчетов, и затем используются для аппроксимации поверхностей потенциальной энергии. Это позволяет значительно сократить время вычислений, сохраняя при этом приемлемый уровень точности, что делает возможным моделирование систем большего размера и в течение более длительных временных интервалов. Фактически, MLIP позволяют заменить прямые вычисления квантово-химических расчетов на более быстрые, но приближенные оценки, основанные на обученной модели.
Успех машинного обучения межatomных потенциалов (MLIP) напрямую зависит от качества обучающих данных. Однако, на практике, наборы данных, используемые для обучения MLIP, часто содержат шум, происходящий из-за погрешностей и приближений, присущих первопричинным квантово-химическим расчетам, на основе которых эти данные генерируются. Ошибки, возникающие в процессе расчета энергии, сил и других свойств, могут приводить к неточностям в обученных потенциалах и, как следствие, к снижению точности и надежности молекулярно-динамических симуляций, построенных на их основе. Особенно критичен шум в данных, используемых для обучения потенциалов, описывающих химические реакции или фазовые переходы, где даже небольшие погрешности могут приводить к значительным ошибкам в предсказаниях.
Продвинутые фреймворки, такие как MACE, расширяют возможности MLIP (Machine Learning Interatomic Potentials) за счет использования эквивариантных архитектур. Эквивариантность обеспечивает, что предсказания модели инвариантны к операциям симметрии, таким как вращения и перестановки атомов, что критически важно для физически корректного моделирования. В отличие от стандартных нейронных сетей, эквивариантные модели обучаются представлять физические свойства непосредственно в форме, не зависящей от выбора системы координат, что приводит к улучшению обобщающей способности и повышению точности предсказаний энергии и сил между атомами, особенно при экстраполяции на новые конфигурации и составы материалов. Это позволяет проводить более эффективные и надежные молекулярно-динамические симуляции.
Борьба с Шумом: От Ручного Фильтрации к Динамическим Подходам
Традиционные методы снижения шума, такие как ручная фильтрация данных, требуют значительных трудозатрат и времени специалистов для анализа и исправления каждого подозрительного значения. Этот процесс становится особенно неэффективным при работе с большими объемами данных, характерными для современных задач машинного обучения и анализа, где ручной анализ просто не масштабируется. В отличие от автоматизированных подходов, ручная фильтрация не позволяет оперативно адаптироваться к изменяющимся характеристикам шума и требует постоянного вмешательства человека, что ограничивает возможности автоматизации и снижает производительность системы.
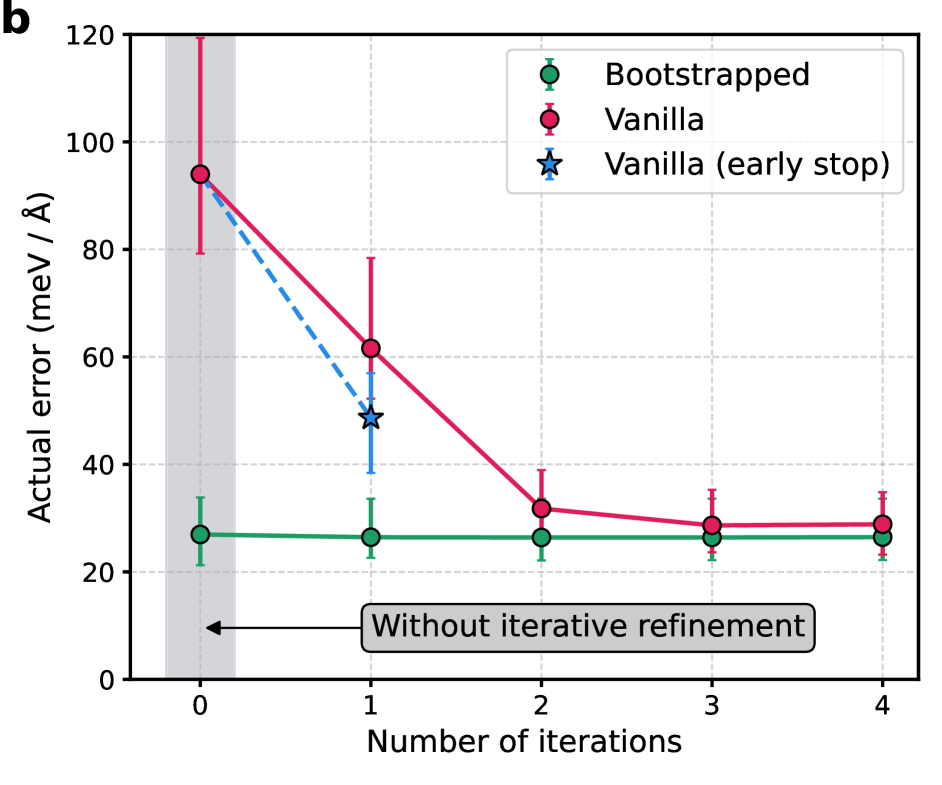
Метод Итеративной Уточнения представляет собой автоматизированный подход к снижению уровня шума в данных, однако его реализация подразумевает многократное повторение циклов обучения и фильтрации. Каждый цикл включает в себя переобучение модели на отфильтрованных данных, что приводит к существенным вычислительным затратам, особенно при работе с большими объемами информации. Несмотря на автоматизацию, суммарное время, необходимое для завершения всех итераций, может значительно превышать время, затрачиваемое на ручную фильтрацию небольших наборов данных, что ограничивает масштабируемость данного метода для задач, требующих обработки данных в реальном времени или больших масштабах.
Методика динамического снижения шума, основанная на сочетании обнаружения выбросов «на лету» и экспоненциального скользящего среднего, позволяет в процессе обучения модели идентифицировать и снижать влияние подозрительных точек данных. Обнаружение выбросов происходит в реальном времени, без необходимости предварительной обработки или ручной фильтрации. Экспоненциальное скользящее среднее, в свою очередь, позволяет плавно уменьшать вес точек, классифицированных как выбросы, минимизируя их влияние на процесс обучения и обеспечивая более стабильную и эффективную сходимость модели. Такой подход позволяет снизить вычислительные затраты по сравнению с итеративной фильтрацией и повысить точность модели за счет исключения из обучения нерелевантных или ошибочных данных.
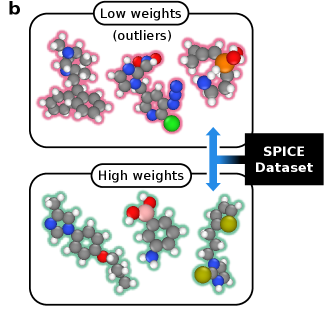
Метод динамической загрузки (Dynamic Bootstrapping) повышает эффективность обучения за счет адаптивного взвешивания вкладов потерь, основанного на вероятности данных. В ходе тестирования на наборе данных SPICE 2.0, применение данной методики позволило добиться в три раза меньшего уровня ошибок в оценке энергии по сравнению с базовой моделью, что свидетельствует о значительном улучшении точности и надежности прогнозов.
Проверка Надежности и Широкая Применимость Устойчивых MLIP
Для подтверждения надежности и точности разработанных моделей машинного обучения потенциалов (MLIPs), обученных с применением методов снижения шума, проведена валидация на общепринятых эталонных наборах данных, таких как revMD17 и SPICE 2.0. Оценка производилась с использованием метрики среднеквадратичной ошибки (RMSE), позволяющей количественно оценить расхождение между предсказанными и фактическими значениями энергии. Полученные результаты демонстрируют высокую степень соответствия между предсказаниями моделей и эталонными данными, что свидетельствует об их способности к обобщению и надежной работе в различных условиях. Применение этих методов валидации критически важно для обеспечения достоверности результатов моделирования и прогнозирования свойств материалов и химических соединений.
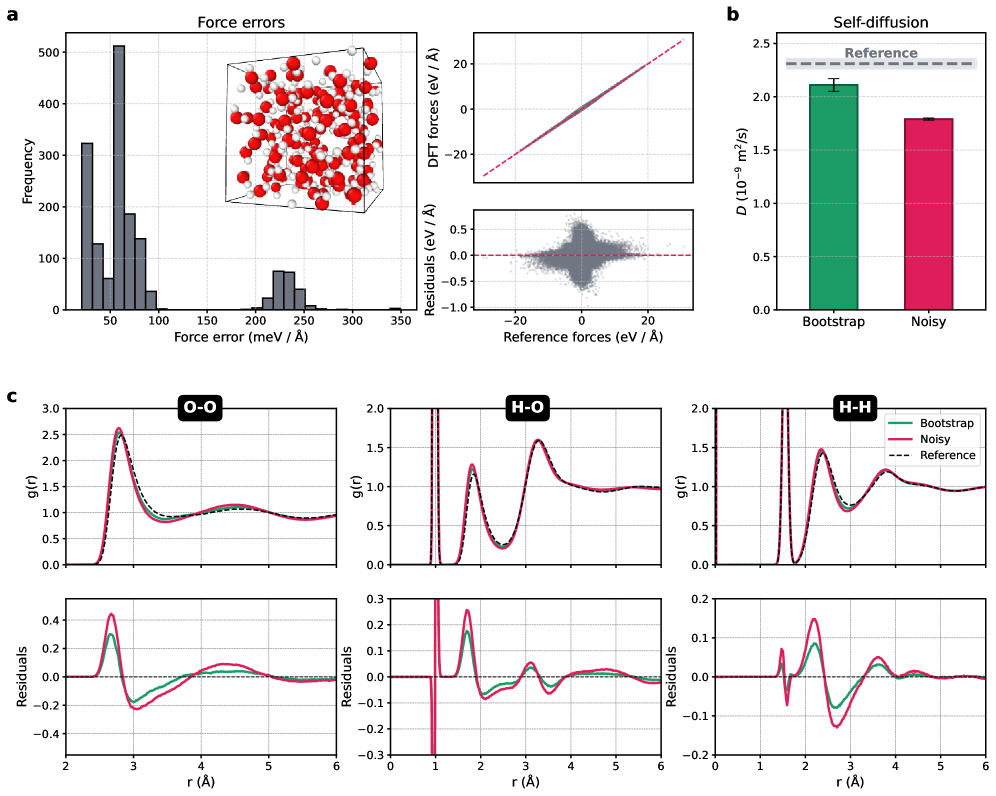
Разработанные модели машинного обучения, устойчивые к шумам, продемонстрировали высокую точность валидации на наборе данных revMD17, достигнув среднеквадратичной ошибки RMSE в диапазоне 25-30 мэВ/Å. Такая точность свидетельствует о значительном улучшении обобщающей способности моделей и позволяет проводить надежное моделирование сложных систем, в частности, симуляции воды. Проведенные расчеты показали, что коэффициент диффузии воды, полученный с использованием этих моделей, составляет 2.11 \times 10^{-9} \text{ м}^2/\text{с}, что отличается от эталонного значения всего на 0.20 \times 10^{-9} \text{ м}^2/\text{с}. Это подтверждает возможность применения разработанного подхода для получения достоверных результатов в различных областях материаловедения и химии.
В результате проведенного моделирования воды был получен коэффициент диффузии, равный 2.11 \times 10^{-9} \text{ м}^2/\text{с}. При этом, отклонение от эталонного значения составило всего 0.20 \times 10^{-9} \text{ м}^2/\text{с}. Такое незначительное расхождение подтверждает высокую точность и надежность разработанных методов машинного обучения в предсказании динамических свойств жидкостей, что открывает возможности для проведения детальных исследований и моделирования сложных водных систем в различных областях науки и техники.
Разработанные методики, изначально предназначенные для повышения точности предсказания свойств материалов, оказались применимы в гораздо более широком контексте, формируя своего рода фундаментальную модель для различных задач материаловедения и химии. Принципы, лежащие в основе устойчивого обучения моделей, позволяют создавать универсальные инструменты, способные адаптироваться к различным наборам данных и типам систем. Это означает, что полученные модели не ограничиваются конкретными наборами данных, такими как revMD17 или SPICE 2.0, а могут быть использованы для моделирования широкого спектра химических соединений и материалов, значительно расширяя возможности компьютерного моделирования и открывая новые перспективы для научных исследований и разработки инновационных технологий. Подобный подход позволяет перейти от создания специализированных моделей к разработке универсальных инструментов, способных решать широкий круг задач в материаловедении и химии.
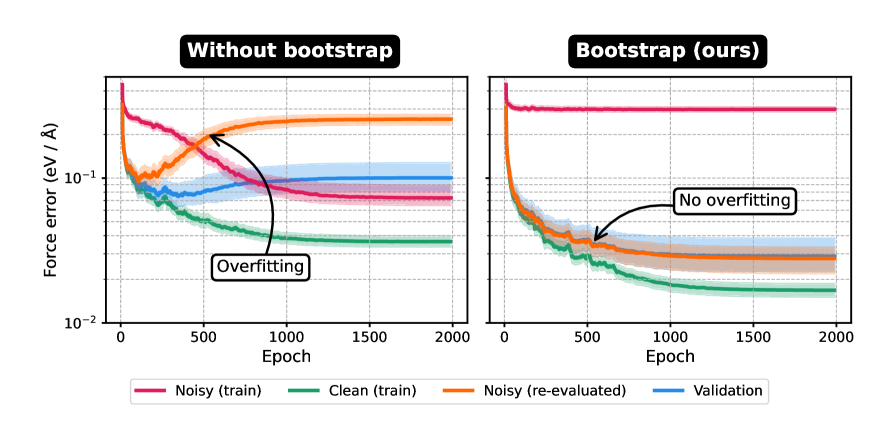
Исследование демонстрирует, что динамический отбор данных, осуществляемый в процессе обучения потенциалов, позволяет существенно повысить устойчивость модели к шумам. По сути, система непрерывно проверяет и корректирует свои правила, отбрасывая нерелевантные данные. Как заметил Джон Стюарт Милль: «Свобода состоит в возможности делать то, что не мешает другим». В данном контексте, «свобода» модели проявляется в её способности игнорировать шумные данные, не искажая общую картину и, следовательно, обучаясь более эффективно. Этот подход к отбору данных, по сути, является реверс-инжинирингом реальности, позволяющим выявить и отсеять нежелательные помехи, тем самым приближая модель к истинному представлению о межмолекулярных взаимодействиях. Каждый отфильтрованный выброс — философское признание несовершенства исходных данных.
Что дальше?
Представленный подход к отсеву выбросов, основанный на динамическом бутстрапинге, безусловно, расширяет границы устойчивости обучения межатомных потенциалов. Однако, что произойдёт, если шум в данных не случаен, а систематичен — следствие фундаментальных ограничений самого метода моделирования? Простое отбрасывание «плохих» данных может привести к игнорированию критически важных физических явлений, замаскированных под шум. Необходимо исследовать методы, позволяющие не просто отфильтровывать, а интерпретировать шум, извлекая из него информацию о недостатках самой модели или исходных предположений.
Более того, акцент на устойчивости обучения — это лишь одна сторона медали. Что если истинная сила “фундаментальных моделей” заключается не в их способности игнорировать шум, а в способности учиться на нём? Представьте систему, способную адаптировать свою структуру и параметры, чтобы компенсировать неточности данных, превращая их в новые возможности. Вместо борьбы с шумом, необходимо научиться его использовать, создавая модели, которые не просто предсказывают, но и понимают границы своей применимости.
И, наконец, стоит задуматься: а не является ли сама концепция “выброса” — произвольной? Что если каждое отклонение от “нормы” содержит в себе ключ к новым открытиям, к расширению границ нашего понимания? Отказ от жёстких критериев отсева, переход к более гибким и адаптивным алгоритмам обучения — вот, возможно, путь к созданию поистине интеллектуальных систем.
Оригинал статьи: https://arxiv.org/pdf/2602.08849.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- SOL ПРОГНОЗ. SOL криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- SUI ПРОГНОЗ. SUI криптовалюта
- FARTCOIN ПРОГНОЗ. FARTCOIN криптовалюта
- HYPE ПРОГНОЗ. HYPE криптовалюта
2026-02-11 04:19