Автор: Денис Аветисян
В статье показано, что современные задачи кластеризации можно эффективно решать, отказавшись от сложных нейронных сетей и используя распределенный подход к определению кластеров.
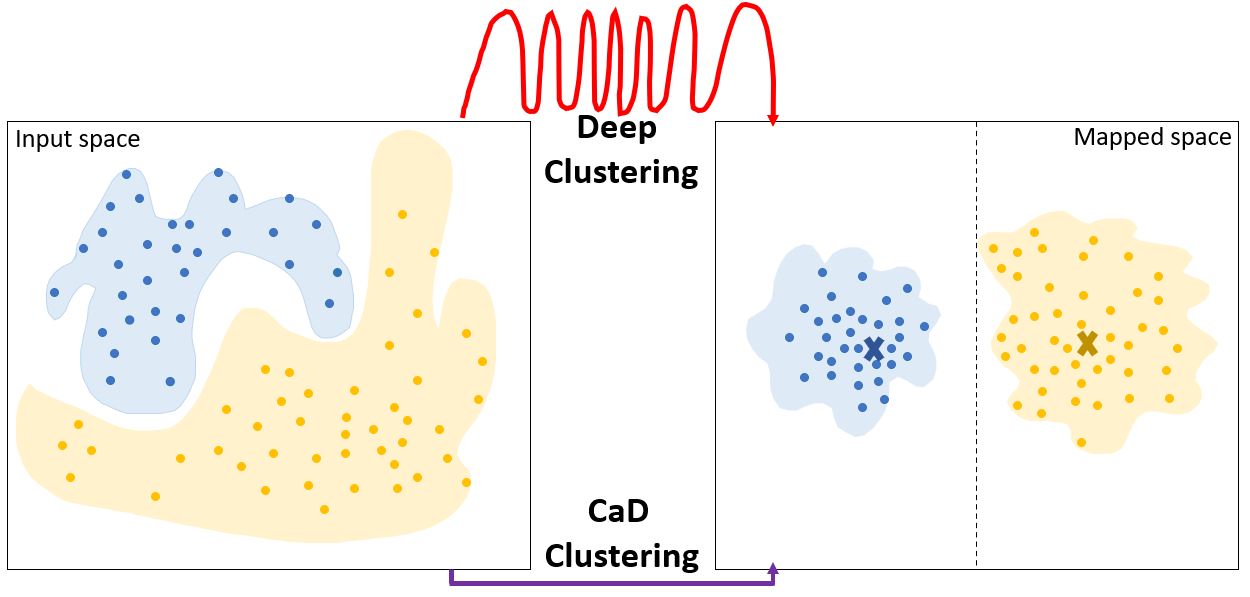
Исследование демонстрирует, что метод Cluster-as-Distribution (CaD) обеспечивает сопоставимую или превосходящую производительность по сравнению с глубоким обучением, особенно при работе с многомерными данными.
Несмотря на заявленные преимущества глубокого кластеризации перед классическим алгоритмом k-средних, ее эффективность часто демонстрируется лишь на изображениях, оставляя неясным, решает ли она фундаментальные ограничения последнего. В работе, озаглавленной ‘How to Achieve the Intended Aim of Deep Clustering Now, without Deep Learning’, исследуется, способно ли глубокое обучение преодолеть неспособность k-средних выявлять кластеры произвольной формы, размера и плотности. Полученные результаты показывают, что подход, основанный на представлении кластеров как распределений (Cluster-as-Distribution), позволяет достичь сравнимой или превосходящей производительности без использования сложных методов представления данных. Может ли учет распределения данных стать ключевым фактором в разработке более эффективных и интерпретируемых алгоритмов кластеризации?
Ограничения Традиционных Подходов к Кластеризации
Традиционные методы кластеризации, в частности, алгоритм k-средних, основываются на измерении схожести между отдельными точками данных. В основе этих алгоритмов лежит предположение о том, что каждая точка представляет собой самостоятельную сущность, и принадлежность к кластеру определяется минимальным расстоянием до центроида. Данный подход эффективно работает с четко разделенными группами, однако сталкивается с трудностями при анализе данных, где границы между кластерами размыты или определяются не только расстоянием, но и более сложными взаимосвязями. В результате, классические алгоритмы кластеризации могут упускать из виду важные структуры в данных, особенно когда объекты связаны между собой и формируют сложные взаимозависимости, выходящие за рамки простого измерения расстояния между отдельными точками.
Традиционные методы кластеризации, такие как k-средних, испытывают значительные трудности при работе со сложными данными, где границы между группами размыты или нечетко определены. В таких случаях, применение простых метрик расстояния, лежащих в основе этих алгоритмов, приводит к неточным результатам и ошибочной интерпретации данных. Например, в задачах анализа изображений или обработки естественного языка, объекты могут иметь сложные взаимосвязи и принадлежать одновременно к нескольким категориям, что делает невозможным их четкое разделение на основе единой дистанции. Вместо этого, требуется учитывать контекст и взаимосвязи между данными, что выходит за рамки возможностей стандартных алгоритмов кластеризации, ориентированных на поиск компактных и хорошо разделенных групп.
Существуют фундаментальные ограничения, присущие многим методам кластеризации, которые не позволяют выявлять определенные типы скрытой структуры данных. Традиционные алгоритмы, ориентированные на поиск компактных групп на основе расстояния между точками, часто терпят неудачу, когда данные обладают сложной иерархией, нелинейными взаимосвязями или высокой плотностью. Например, данные, формирующие перекрывающиеся или вложенные кластеры, могут быть неправильно интерпретированы как единая масса, поскольку алгоритмы, основанные на простой метрике расстояния, не способны различать сложные паттерны. Это связано с тем, что многие методы кластеризации предполагают, что кластеры имеют четкие границы и сферическую форму, что далеко не всегда соответствует реальным данным. Таким образом, при анализе сложных наборов данных необходимо учитывать ограничения традиционных подходов и рассматривать альтернативные методы, способные выявлять более тонкие и сложные структуры.
Кластеры как Распределения: Новый Взгляд на Структуру Данных
Кластеризация, основанная на представлении кластеров как распределений, представляет собой новый подход, в котором кластеры определяются не как наборы дискретных точек, а как вероятностные распределения. Вместо того, чтобы рассматривать принадлежность точки к кластеру как бинарное решение, данный подход оценивает вероятность того, что точка принадлежит определенному распределению, что позволяет более точно моделировать данные с неоднозначными или перекрывающимися кластерами. Такое представление особенно полезно при работе с данными высокой размерности или нечеткими границами между кластерами, где традиционные методы, основанные на расстоянии до центроидов, могут быть неэффективными. Определение кластеров через распределения позволяет учитывать не только местоположение точек, но и их плотность и форму, что обеспечивает более гибкое и точное моделирование структуры данных.
В подходе, основанном на распределениях, для оценки схожести между распределениями используются распределительные ядра (Distributional Kernels). В отличие от точечных сравнений, которые оценивают близость отдельных точек данных, распределительные ядра учитывают всю форму распределения, позволяя выявлять более тонкие взаимосвязи. Это достигается путем определения ядра, которое измеряет расстояние между двумя распределениями на основе их статистических свойств, таких как среднее значение, дисперсия и другие моменты. Использование таких ядер позволяет более эффективно кластеризовать данные, когда отдельные точки могут быть близки друг к другу, но их распределения значительно отличаются, или наоборот.
Метод Kernel-Based Clustering (KBC) расширяет подход, основанный на распределениях, используя Kernel Mean Embedding для представления этих распределений в пространстве признаков. Это позволяет эффективно выполнять кластеризацию, поскольку операции над распределениями сводятся к операциям над векторами в этом пространстве. Экспериментальные данные, полученные на 1024-мерном наборе данных COIL-20, демонстрируют превосходную производительность метода KBC, подтвержденную значениями Normalized Mutual Information (NMI) в 0.98. Данный показатель свидетельствует о высокой степени соответствия между полученными кластерами и истинными метками данных.
Глубокое Обучение для Выделения Информативных Признаков
Метод глубокой кластеризации использует обучение представлений (Representation Learning) для извлечения информативных признаков из данных, что значительно повышает эффективность применения методов распределенной кластеризации. В отличие от традиционных подходов, которые полагаются на ручное проектирование признаков или линейные преобразования, обучение представлений позволяет автоматически выявлять и кодировать сложные зависимости в данных. Это особенно важно для высокоразмерных данных, где ручной выбор признаков становится затруднительным, а алгоритмы глубокого обучения способны эффективно уменьшать размерность и выделять наиболее релевантные характеристики для последующей кластеризации.
Методы DEC (Deep Embedded Clustering) и IDEC (Improved Deep Embedded Clustering) используют автоэнкодеры для обучения компактным представлениям данных, снижая размерность исходного пространства признаков. В процессе обучения, автоэнкодеры не только сжимают данные, но и одновременно оптимизируют назначение кластеров, используя расхождение Кульбака-Лейблера (KL Divergence) в качестве функции потерь. KL Divergence заставляет распределение признаков внутри каждого кластера приближаться к единичному гауссовскому распределению, тем самым улучшая разделение между кластерами и способствуя формированию более четких и компактных кластеров. Оптимизация происходит итеративно, одновременно уточняя веса автоэнкодера и центры кластеров.
При работе с данными высокой размерности, методы глубокого обучения демонстрируют значительное преимущество в преодолении проблемы «проклятия размерности» и выявлении скрытых закономерностей. Однако, на наборе данных w100Gaussians, метод KBC (Kernel-Based Clustering) последовательно превосходит все протестированные подходы глубокого и традиционного кластеризации, достигая идеальных показателей NMI (Normalized Mutual Information). В то время как другие методы испытывают затруднения в выделении кластеров в данных высокой размерности, KBC обеспечивает точное разделение и достигает максимального значения NMI, что подтверждает его эффективность в данной задаче.

Контрастивное Обучение: Путь к Более Надежным Кластерам
Контрастное кластеризование представляет собой перспективный подход к обучению устойчивых признаков и представлений кластеров, основанный на принципе взаимного притяжения схожих точек данных и отталкивания различных. Данный метод позволяет алгоритмам не просто группировать объекты по заданным признакам, но и выявлять скрытые закономерности в данных, формируя более точные и обобщенные представления о структуре данных. По сути, алгоритм «обучается» отличать объекты, принадлежащие к одному кластеру, от тех, что находятся вне его, что значительно повышает надежность и качество кластеризации, особенно в условиях зашумленных или неполных данных. Такой подход позволяет создавать более устойчивые к изменениям и обобщающие модели, способные эффективно анализировать и интерпретировать сложные наборы данных.
Методы контрастивного обучения, применяемые в кластеризации, позволяют создавать представления данных, которые отражают их внутреннюю структуру. Вместо простого сопоставления точек на основе поверхностных признаков, эти подходы стремятся выделить ключевые закономерности и связи, определяющие группировку объектов. Благодаря этому, алгоритмы способны не только повысить точность кластеризации на имеющемся наборе данных, но и значительно улучшить способность к обобщению — то есть, успешно работать с новыми, ранее не встречавшимися данными. Такой подход особенно важен в задачах, где данные постоянно меняются или их объем огромен, поскольку позволяет алгоритму адаптироваться и поддерживать высокую производительность даже в сложных условиях.
Современные достижения в области кластеризации, в частности, применение контрастивного обучения, открывают новые перспективы для интеллектуального анализа данных и принятия решений в различных областях. Так, разработанный метод KBC продемонстрировал впечатляющие результаты на наборе данных Tutorial по одноклеточной транскриптомике, достигнув показателя NMI в 0.87. Данный результат существенно превосходит показатели, полученные альтернативными подходами IDEC и CC, которые практически не смогли выделить значимые кластеры, зафиксировав значения NMI близкие к нулю. Подобный прогресс указывает на потенциал новых методов для более точной и эффективной обработки сложных биологических данных и, в конечном итоге, для углубленного понимания фундаментальных процессов.
Исследование демонстрирует, что для достижения эффективного кластеризования не всегда требуется сложность глубокого обучения. Подход «Кластер как распределение» (CaD) позволяет достичь сопоставимых, а иногда и лучших результатов, особенно в высокоразмерных данных, за счет более простой и понятной логики. Как заметил Бертран Рассел: «Чем больше я узнаю людей, тем больше я люблю собак». Эта фраза, на первый взгляд, не связана с кластеризацией, но отражает важный принцип: иногда простота и естественность решения превосходят сложные и искусственные конструкции. В данном случае, CaD предлагает элегантный путь к кластеризации, фокусируясь на базовых принципах, что соответствует идее поиска баланса между сложностью и эффективностью.
Куда двигаться дальше?
Представленные результаты, несомненно, заставляют задуматься о чрезмерном увлечении сложностью в области кластеризации. Попытки «научить» алгоритмы извлекать признаки, казалось бы, необходимы, но текущая работа демонстрирует, что элегантность простоты может быть не менее эффективной, а иногда и превосходящей. Однако, это не означает, что задача решена. Остаётся неясным, насколько хорошо подход, основанный на представлении кластеров как распределений, масштабируется к данным, чья внутренняя структура принципиально отличается от рассмотренных в данной работе — к данным с сильной неравномерностью плотности или сложными взаимосвязями между признаками.
Дальнейшие исследования должны быть направлены на понимание границ применимости данного подхода. Необходимо изучить, как различные ядра, используемые в построении распределений, влияют на качество кластеризации в различных сценариях. Интересным направлением представляется комбинация данного подхода с методами понижения размерности, не основанными на глубоком обучении, для повышения устойчивости и эффективности в условиях высокой размерности данных. По сути, речь идёт о поиске оптимального баланса между простотой модели и её способностью к обобщению.
В конечном счете, необходимо помнить, что кластеризация — это не просто математическая задача, а инструмент для понимания структуры данных. Стремление к «лучшему» алгоритму должно быть подкреплено пониманием того, что истинная ценность заключается в интерпретируемости и применимости полученных результатов. Сложность ради сложности — это путь в никуда.
Оригинал статьи: https://arxiv.org/pdf/2602.05749.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- SOL ПРОГНОЗ. SOL криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- Акции Южуралзолото ГК прогноз. Цена акций UGLD
- FARTCOIN ПРОГНОЗ. FARTCOIN криптовалюта
- SUI ПРОГНОЗ. SUI криптовалюта
2026-02-08 05:29