Эволюция на Финансовых Рынках: Моделирование Экосистем Агентов

Автор: Денис Аветисян

Новый подход к анализу финансовых рынков рассматривает их как развивающиеся экосистемы, где стратегии агентов эволюционируют в условиях конкуренции и взаимодействия.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал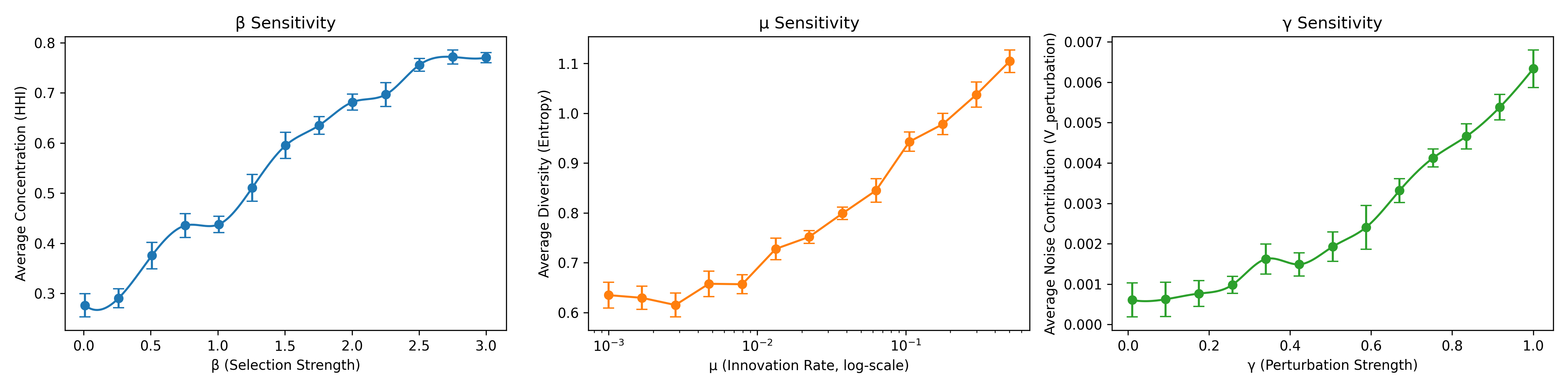

Анализ чувствительности эволюционных параметров, проведенный на симуляции от 7 июля 2025 года, выявил, что сила отбора β оказывает влияние на концентрацию рынка, скорость инноваций μ - на разнообразие стратегий, а интенсивность возмущений γ - на вклад в волатильность, при этом 95%-ные доверительные интервалы, рассчитанные на основе 128 прогонов, позволяют оценить стабильность полученных результатов. — Анализ чувствительности эволюционных параметров, проведенный на симуляции от 7 июля 2025 года, выявил, что сила отбора β оказывает влияние на концентрацию рынка, скорость инноваций μ — на разнообразие стратегий, а интенсивность возмущений γ — на вклад в волатильность, при этом 95%-ные доверительные интервалы, рассчитанные на основе 128 прогонов, позволяют оценить стабильность полученных результатов.

Представлен FinEvo — фреймворк, моделирующий динамику финансовых рынков с использованием эволюционной теории игр и агент-ориентированного моделирования для оценки системных рисков и эффективности регуляторных мер.

Традиционные подходы к оценке финансовых стратегий, основанные на изолированных бэктестах, не учитывают сложные взаимодействия и эволюцию рыночных условий. В данной работе представлена платформа ‘FinEvo: From Isolated Backtests to Ecological Market Games for Multi-Agent Financial Strategy Evolution’, моделирующая финансовые рынки как динамичные экосистемы, где разнородные агенты, использующие методы машинного обучения, адаптируются и конкурируют друг с другом. Предложенный подход позволяет исследовать эволюционные закономерности, невидимые при статическом анализе, и выявлять паттерны формирования коалиций и краха стратегий. Возможно ли с помощью подобной экосистемной моделирования предсказать влияние макроэкономической политики и регулирования на эволюцию рыночных цен и достижение равновесия?

Моделирование рынков как развивающихся экосистем

Традиционные финансовые модели зачастую строятся на статичных предположениях, игнорируя сложную и постоянно меняющуюся природу взаимодействия участников рынка. Данный подход, хоть и упрощает расчеты, не позволяет адекватно отразить влияние поведенческих факторов, адаптации стратегий и появления новых игроков. В результате, такие модели могут давать неверные прогнозы, особенно в периоды высокой волатильности или при возникновении системных рисков. Неспособность учесть динамику взаимодействия между трейдерами, инвесторами и другими участниками рынка приводит к искажению реальной картины и снижает эффективность принимаемых решений, что особенно критично в условиях современной финансовой системы.

Подход FinEvo представляет собой инновационную методологию, рассматривающую финансовые рынки как сложные, эволюционирующие экосистемы, вдохновленную принципами биологии. В отличие от традиционных моделей, опирающихся на статические предположения, FinEvo моделирует взаимодействие участников рынка как конкуренцию и кооперацию, подобно видам в естественной среде. Это позволяет учитывать адаптацию к изменяющимся условиям, появление новых стратегий и непредсказуемые эффекты, которые часто приводят к системным рискам. Таким образом, FinEvo не только предоставляет более реалистичное представление о финансовых процессах, но и является важным шагом на пути к лучшему пониманию и прогнозированию кризисных явлений, открывая возможности для разработки более устойчивых и эффективных финансовых систем.

Гетерогенность: Двигатель рыночного поведения

В FinEvo используется популяция “гетерогенных агентов”, представляющих собой разнообразные стратегии торговли и наборы информации. Каждый агент в модели обладает уникальным алгоритмом принятия решений, основанным на различных подходах к анализу рынка и интерпретации данных. Различия между агентами касаются не только используемых торговых стратегий (например, следование за трендом, усреднение стоимости, арбитраж), но и источников информации, доступных каждому агенту — от публичных рыночных данных до частной информации, полученной через симуляцию инсайдерской торговли. Такое разнообразие агентов позволяет моделировать более реалистичное поведение рынка, учитывая взаимодействие различных типов трейдеров и их реакцию на изменяющиеся условия.

В составе модели FinEvo агенты представлены различными типами, что обеспечивает разнообразие стратегий. Среди них выделяются агенты, основанные на правилах, реализующие технический анализ рыночных данных для принятия решений о торговле. Также присутствуют информированные трейдеры, использующие закрытую информацию, недоступную другим участникам, для получения преимущества. Наряду с ними используются более сложные агенты, основанные на глубоком обучении, способные выявлять закономерности и корреляции в исторических данных, что позволяет им адаптироваться к изменяющимся рыночным условиям и прогнозировать будущие движения цен.

Включение агентов, использующих обучение с подкреплением (Reinforcement Learning) и больших языковых моделей (LLM-Based Agents), значительно расширяет поведенческий репертуар модели FinEvo. Агенты на основе обучения с подкреплением способны адаптировать свои торговые стратегии на основе получаемого опыта и вознаграждения, оптимизируя поведение для достижения заданных целей. LLM-агенты, в свою очередь, используют возможности обработки естественного языка для анализа новостных потоков, социальных сетей и других текстовых источников, что позволяет им выявлять закономерности и принимать решения на основе более широкого контекста. Комбинация этих подходов обеспечивает динамическую адаптацию к изменяющимся рыночным условиям и способствует более реалистичному моделированию поведения участников рынка.

Ранжирование агентов показывает, что их производительность существенно различается в зависимости от бычьего или медвежьего рынка.

От теории к симуляции: FinEvo Framework

В основе FinEvo лежит стохастическое дифференциальное уравнение $FinEvo\ SDE$ , описывающее динамику популяций агентов во времени. Данное уравнение моделирует эволюцию численности и характеристик агентов как непрерывный процесс, подверженный случайным флуктуациям. Формально, $FinEvo\ SDE$ представляет собой уравнение вида $dX_t = \mu(X_t)dt + \sigma(X_t)dW_t$ , где $X_t$ — состояние популяции в момент времени $t$ , $\mu(X_t)$ — дрифт, определяющий среднюю скорость изменения популяции, $\sigma(X_t)$ — коэффициент диффузии, отражающий степень случайности, а $dW_t$ — винеровский процесс, моделирующий случайные воздействия. Использование непрерывного времени позволяет более точно описывать процессы адаптации и конкуренции между агентами в финансовых рынках.

Для практической реализации $FinEvo\ SDE$ используется метод дискретизации, известный как ‘Дискретное моделирование’. Этот подход преобразует непрерывное уравнение в дискретный алгоритм, позволяющий выполнять вычисления с использованием конечного числа шагов по времени. Дискретизация значительно снижает вычислительную сложность, делая возможным моделирование динамики рынка с большим количеством агентов и на длительных временных горизонтах. Выбор конкретного метода дискретизации (например, схема Эйлера или более сложные схемы Рунге-Кутты) влияет на точность и стабильность моделирования, однако позволяет достичь компромисса между точностью и скоростью вычислений, необходимым для эффективного анализа эволюционных процессов на рынке.

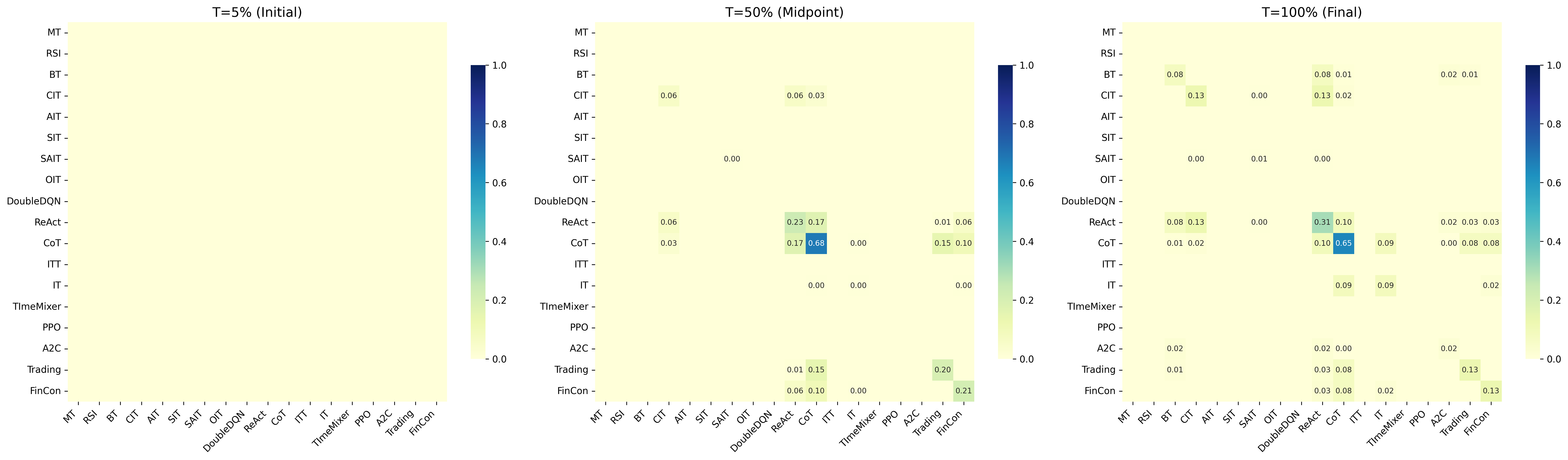
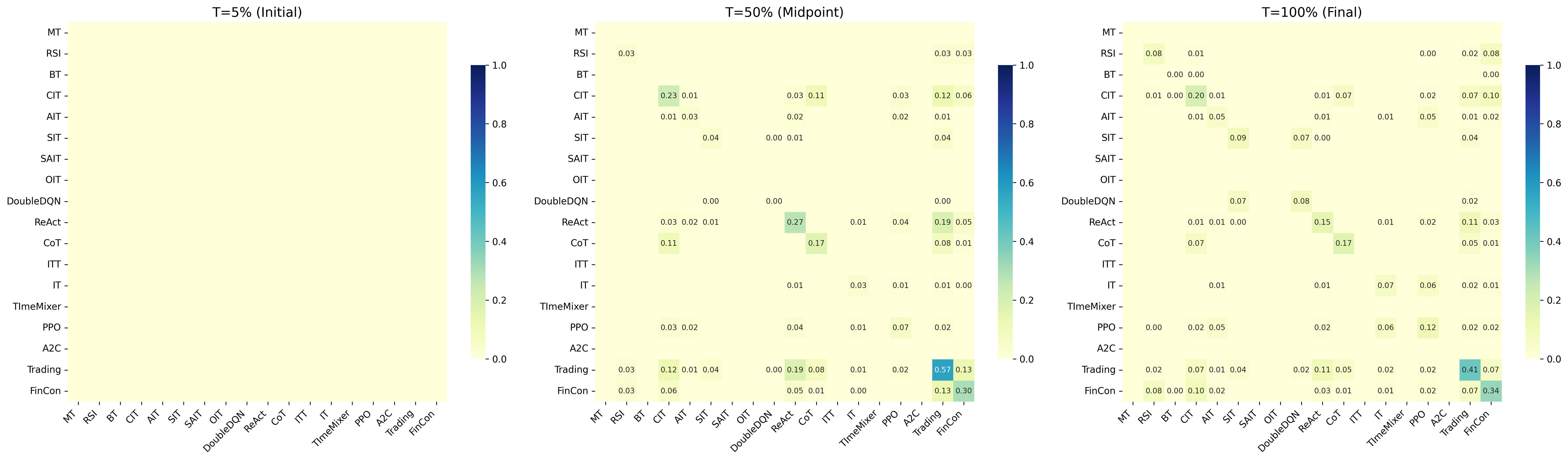
В рамках FinEvo, изучение эволюционной динамики позволяет анализировать процессы адаптации, конкуренции и выживания торговых стратегий в моделируемой рыночной среде. Данный подход позволяет отслеживать изменения в популяциях стратегий на протяжении времени, определяя факторы, влияющие на их успех или неудачу. Наблюдение за взаимодействием стратегий, включая их способность к мутации и рекомбинации, позволяет выявить доминирующие паттерны поведения и предсказать долгосрочные тенденции в эволюции торговых алгоритмов. Анализ включает количественную оценку показателей эффективности различных стратегий и выявление корреляций между их параметрами и рыночными условиями, что способствует оптимизации и разработке более устойчивых и прибыльных алгоритмов.

Анализ матрицы совместной встречаемости стратегий показывает, что положительный шок приводит к увеличению частоты одновременного использования доминирующих стратегий на всех этапах развития.

Эмерджентная динамика и системная устойчивость

В рамках моделирования FinEvo наблюдаются явления, демонстрирующие спонтанное возникновение сложных паттернов поведения. Симуляции выявляют тенденцию к концентрации рыночной доли у отдельных агентов, что может приводить к доминированию и снижению конкуренции. Одновременно с этим, агенты проявляют диверсификацию стратегий, адаптируясь к изменяющимся условиям и ища новые возможности. Однако, эти процессы не всегда приводят к стабильности; моделирование также показывает потенциал для возникновения системного риска, когда локальные неудачи могут распространяться по всей системе, что подчеркивает важность анализа подобных динамических процессов для понимания устойчивости и хрупкости финансовых рынков.

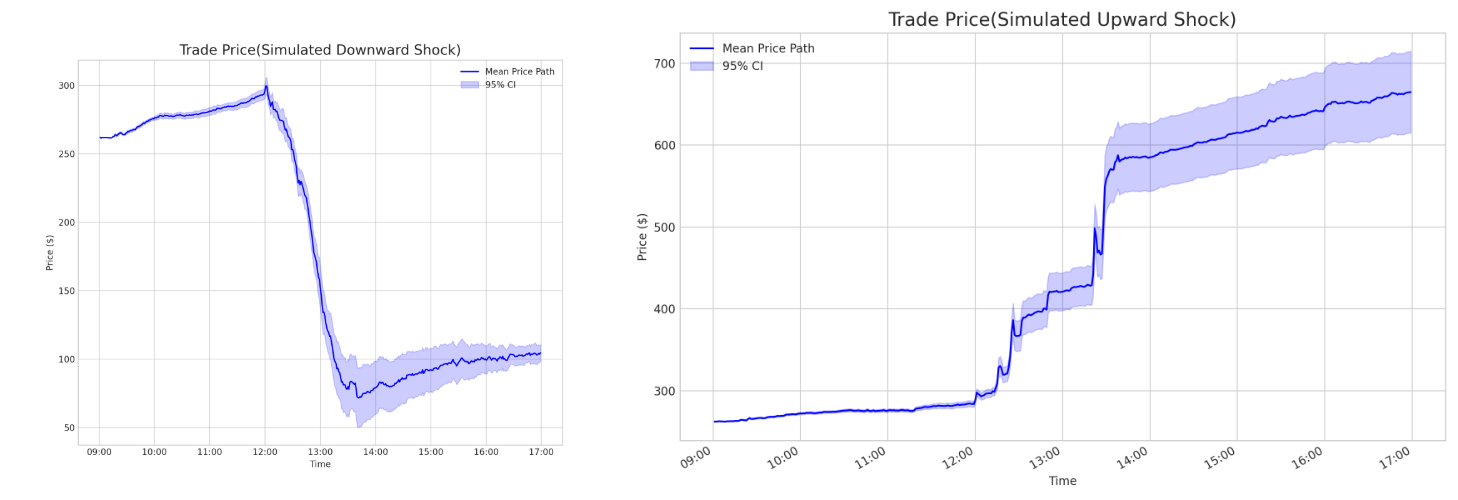
Исследования в рамках FinEvo продемонстрировали выдающуюся устойчивость системы к различным возмущениям. Моделирование показало, что даже при значительных изменениях в параметрах поведения отдельных агентов и при колебаниях рыночных условий, система в целом сохраняет свою функциональность и способность к адаптации. Эта робастность объясняется сложной сетью взаимодействий между агентами и способностью системы к самоорганизации, позволяющей ей компенсировать негативные эффекты внешних воздействий. Наблюдаемая устойчивость к пертурбациям подчеркивает потенциал FinEvo как ценного инструмента для изучения динамики сложных систем и разработки стратегий повышения их надежности в условиях неопределенности.

Представленная в данной работе платформа FinEvo обеспечивает мощный инструмент для анализа системного риска и оценки эффективности различных политических мер. Исследование позволяет ученым моделировать сложные финансовые системы и прогнозировать их реакцию на внешние воздействия и вмешательства. Благодаря возможности варьировать параметры агентов и условия рынка, становится возможным оценить, как конкретные регуляторные изменения или экономические стимулы могут повлиять на стабильность всей системы. Такой подход позволяет не только выявлять потенциальные источники риска, но и разрабатывать более эффективные стратегии управления ими, что особенно важно в контексте быстро меняющихся финансовых ландшафтов и необходимости предотвращения масштабных кризисов.

После негативного шока структура альянсов восстанавливается быстрее, формируя меньше, но более прочных связей, в отличие от сценария с положительным воздействием.

Расширяя горизонты: Будущие направления

Будущие исследования направлены на интеграцию данных высокой частоты в симуляции FinEvo, что позволит значительно повысить их точность и детализацию. Использование данных, получаемых с минимальной задержкой, таких как биржевые котировки в реальном времени, откроет возможность моделирования краткосрочных рыночных колебаний и реакций участников на быстро меняющиеся события. Такой подход позволит более реалистично воспроизводить динамику финансовых рынков, учитывая влияние мельчайших изменений в настроениях инвесторов и потоках капитала. Внедрение данных высокой частоты не только улучшит предсказательную силу модели, но и позволит глубже понять механизмы формирования цен и распространения информации на финансовых рынках, представляя собой значительный шаг вперед в развитии финансового моделирования.

Дальнейшее развитие модели FinEvo предполагает включение эффектов сетевого взаимодействия, что позволит более реалистично отражать сложную картину взаимодействия между участниками финансовых рынков. Исследования направлены на моделирование того, как действия одного агента могут каскадно распространяться по сети, влияя на поведение других и формируя общую динамику рынка. Учет этих сетевых эффектов особенно важен для понимания возникновения и распространения финансовых кризисов, формирования пузырей и других явлений, обусловленных коллективным поведением. Внедрение сетевых моделей позволит не только точнее прогнозировать рыночные тенденции, но и оценивать потенциальное влияние различных факторов на стабильность финансовой системы, открывая новые возможности для разработки эффективных стратегий управления рисками.

Предлагаемые усовершенствования платформы FinEvo призваны закрепить её лидирующие позиции в области моделирования и прогнозирования поведения финансовых рынков. Данная работа формирует основу для новой эры финансового моделирования, позволяя перейти от упрощенных представлений к более реалистичным и детализированным симуляциям. Интеграция высокочастотных данных и учет сетевых эффектов позволят анализировать сложные взаимодействия между участниками рынка с беспрецедентной точностью, что открывает возможности для более эффективного управления рисками и принятия инвестиционных решений. В перспективе, FinEvo может стать незаменимым инструментом для финансовых аналитиков, трейдеров и регуляторов, стремящихся к глубокому пониманию динамики финансовых рынков и предвидению будущих тенденций.

Моделирование внешних шоков показывает, что средняя цена сделки колеблется в пределах <span class="katex-eq" data-katex-display="false"> \pm 3\sigma </span> от среднего значения, отражая диапазон возможных рыночных сценариев. — Моделирование внешних шоков показывает, что средняя цена сделки колеблется в пределах $\pm 3\sigma$ от среднего значения, отражая диапазон возможных рыночных сценариев.

Исследование, представленное в данной работе, демонстрирует, что финансовые рынки представляют собой сложные системы, где поведение отдельных агентов определяет общую динамику. Это перекликается с глубоким пониманием Теслой взаимосвязанности элементов в любой системе. Он говорил: «Самое важное — это не то, что я изобрел, а то, что я помог другим изобрести». Подобно тому, как Тесла видел потенциал в других изобретателях, FinEvo позволяет изучать взаимодействие множества гетерогенных агентов, выявляя emergent behavior и закономерности, которые невозможно обнаружить при изолированном тестировании стратегий. Модель FinEvo, моделируя финансовый рынок как развивающуюся экосистему, позволяет оценить влияние различных стратегий и регулятивных мер на стабильность всей системы, что особенно важно для понимания и управления системным риском.

Что дальше?

Представленная работа, хотя и предлагает новый взгляд на моделирование финансовых рынков как эволюционирующих экосистем, лишь открывает двери для дальнейших исследований. Очевидно, что упрощение реальности всегда сопряжено с потерей нюансов. Стремление к элегантности решения не должно затмевать понимания его ограничений. В частности, вопрос о масштабируемости предложенного подхода — FinEvo — остается открытым. Чем сложнее экосистема агентов, тем труднее становится анализ и предсказание ее поведения. Простота — залог устойчивости, но и неизбежная жертва детализации.

Не менее важным представляется вопрос о валидации модели. Сопоставление результатов, полученных в рамках FinEvo, с реальными данными — задача нетривиальная, учитывая присущую финансовым рынкам стохастичность и непредсказуемость. Необходимо разработать более строгие метрики для оценки адекватности модели и ее способности предсказывать кризисные явления. Иначе говоря, необходимо понять, где заканчивается полезная абстракция и начинается самообман.

В конечном счете, будущее этого направления исследований, вероятно, связано с интеграцией FinEvo с другими подходами, такими как машинное обучение с подкреплением и агент-ориентированное моделирование. Необходимо выйти за рамки чисто экономических моделей и учитывать психологические и социальные факторы, влияющие на поведение агентов. Возможно, тогда удастся создать действительно универсальную модель, способную предсказывать и предотвращать финансовые кризисы. Однако, даже в этом случае, следует помнить: идеальных моделей не существует, а простота часто оказывается более ценной, чем сложность.

Оригинал статьи: https://arxiv.org/pdf/2602.00948.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-03 11:25