Скрытые закономерности нейросетей: извлечение спектральных ядер

Автор: Денис Аветисян

Новый подход позволяет раскрыть интерпретируемые спектральные представления, скрытые в Prior-Data Fitted Networks, обеспечивая понимание механизмов их работы.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал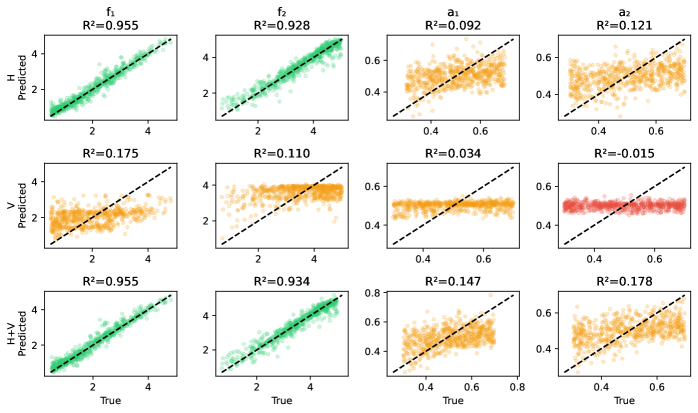

Исследование продемонстрировало, что предсказание частотных параметров <span class="katex-eq" data-katex-display="false"> (f_{1}, f_{2}, a_{1}, a_{2}) </span> достигается с высокой точностью (<span class="katex-eq" data-katex-display="false"> R^{2} > 0.92 </span>), в то время как предсказание амплитуды остаётся слабым (<span class="katex-eq" data-katex-display="false"> R^{2} \approx 0.14 </span>), что обосновывает использование в разработанной архитекте декодера подхода с фильтрбанком для частот и отдельной сети для амплитуды, поскольку, несмотря на возможность извлечения амплитуды, одновременное извлечение всех параметров из весов модели представляется затруднительным. — Исследование продемонстрировало, что предсказание частотных параметров $(f_{1}, f_{2}, a_{1}, a_{2})$ достигается с высокой точностью ( $R^{2} > 0.92$ ), в то время как предсказание амплитуды остаётся слабым ( $R^{2} \approx 0.14$ ), что обосновывает использование в разработанной архитекте декодера подхода с фильтрбанком для частот и отдельной сети для амплитуды, поскольку, несмотря на возможность извлечения амплитуды, одновременное извлечение всех параметров из весов модели представляется затруднительным.

Предлагается фреймворк для автоматического построения ядер на основе анализа спектральной плотности Prior-Data Fitted Networks (PFN).

Непрозрачность внутренних механизмов современных вероятностных моделей затрудняет их интерпретацию и использование в задачах, требующих явного представления ковариационных свойств. В данной работе, посвященной ‘Amortized Spectral Kernel Discovery via Prior-Data Fitted Network’, предложен фреймворк для извлечения интерпретируемых спектральных представлений из сетей, обученных с учетом априорных данных (PFN), позволяющий строить явные ядра без итеративной оптимизации. Ключевым результатом является идентификация латентных выходов внимания в PFN как посредника, связывающего наблюдаемые данные с спектральной структурой, и разработка декодеров для оценки спектральной плотности и соответствующих стационарных ядер посредством теоремы Бохнера. Возможно ли, используя предложенный подход, значительно ускорить и упростить процессы обучения и оптимизации в задачах, требующих точного моделирования ковариационных зависимостей?

Оценка неопределённости: от теории к практике

Традиционные методы машинного обучения часто сосредотачиваются исключительно на получении точечных предсказаний, игнорируя важный аспект — оценку неопределённости. Это упущение может существенно снизить надёжность прогнозов, особенно в критически важных приложениях, где знание о возможных ошибках столь же важно, как и само предсказание. Невозможность количественно оценить уверенность модели в своих результатах затрудняет принятие обоснованных решений и может привести к серьёзным последствиям, например, в медицине или финансах. В отличие от этого, подходы, учитывающие неопределённость, позволяют не только предсказывать значения, но и предоставлять информацию о вероятности различных исходов, что значительно повышает доверие к модели и позволяет более эффективно использовать её результаты. Понимание и количественная оценка неопределённости является ключевым шагом к созданию действительно надёжных и полезных систем машинного обучения.

Гауссовские процессы представляют собой мощный вероятностный подход к решению задач машинного обучения, позволяющий не только предсказывать значения, но и оценивать неопределённость этих предсказаний. Однако, несмотря на свою элегантность и теоретическую обоснованность, применение гауссовских процессов сталкивается с серьёзными вычислительными трудностями. Сложность операций, таких как инвертирование матриц ковариации, растёт кубически с увеличением объёма данных $O(n^3)$ , что делает их непрактичными для работы с большими наборами данных. Это ограничение существенно затрудняет применение гауссовских процессов в современных задачах, где объёмы данных постоянно растут, и требует поиска альтернативных подходов для масштабирования и повышения эффективности вычислений.

Представление ядерных функций через их спектральную плотность открывает возможности для существенного повышения вычислительной эффективности и улучшения интерпретируемости моделей машинного обучения. Вместо работы непосредственно с ядрами, которые требуют $O(n^3)$ операций для больших наборов данных, анализ спектральной плотности позволяет перейти к представлению в частотной области. Это позволяет приблизительно оценить ядро, используя лишь небольшое количество частотных компонент, значительно сокращая вычислительные затраты. Более того, спектральная плотность предоставляет информацию о характеристиках данных в различных масштабах, позволяя выявить доминирующие закономерности и упростить понимание поведения модели. Таким образом, переход к спектральному представлению не только оптимизирует вычисления, но и способствует более глубокому анализу и интерпретации данных, что особенно важно для построения надёжных и прозрачных систем машинного обучения.

Расстояние Вассерштейна между истинными и предсказанными спектральными плотностями уменьшается с увеличением числа выборок GP, демонстрируя компромисс между чёткостью пиков и локализацией частот, который сохраняется при различных значениях ширины полосы σ.

Обучение ядер: от данных к частотному пространству

Глубокое обучение ядрам представляет собой подход к построению ядерных функций, зависящих от данных, посредством итеративной оптимизации. В отличие от статических, заранее определённых ядер, этот метод позволяет адаптировать ядро непосредственно к специфике обучающей выборки. Процесс оптимизации обычно включает определение параметров ядра, максимизирующих некоторую целевую функцию, связанную с производительностью модели в задаче обучения. Итеративный характер алгоритма позволяет постепенно улучшать качество ядра, приближая его к оптимальной форме для данного набора данных. $K(x, x')$ — ядро, параметры которого настраиваются в процессе оптимизации.

Восстановление ядра является ключевым этапом в обучении глубоким ядром. Данный процесс позволяет построить ядро из его спектральной плотности, используя теорему Бохнера. Теорема Бохнера устанавливает, что непрерывная, ограниченная функция, симметричная и неотрицательная, может быть представлена как преобразование Фурье некоторой неотрицательной меры. В контексте восстановления ядра, спектральная плотность, являющаяся преобразованием Фурье ядра, используется для определения самого ядра. Таким образом, $k(x, x') = \in t p(\omega) e^{i \omega (x - x')} d\omega$ , где $k(x, x')$ — ядро, а $p(\omega)$ — спектральная плотность. Эффективное восстановление ядра требует корректного вычисления или аппроксимации спектральной плотности и последующего применения обратного преобразования Фурье.

Переход к анализу проблемы в частотной области позволяет выявить скрытые закономерности в структуре данных, недоступные при прямом рассмотрении в пространстве признаков. Представление ядра в частотной области, посредством его спектральной плотности, упрощает анализ и оптимизацию, поскольку позволяет оперировать с более простыми математическими объектами. Это особенно важно для задач, связанных с высокоразмерными данными, где прямое вычисление и оптимизация ядра может быть вычислительно затратным. Использование преобразования Фурье и связанных с ним методов позволяет эффективно моделировать сложные зависимости в данных и проектировать ядра, адаптированные к конкретным характеристикам входных данных, что приводит к повышению производительности и точности алгоритмов машинного обучения.

Декодер успешно восстанавливает как периодическую структуру, так и пространственную корреляцию спектральных пиков различной сложности, достоверно воспроизводя характерную полосатую структуру и диагональное затухание, что подтверждает его способность точно отражать вторые статистические моменты <span class="katex-eq" data-katex-display="false">S(\omega)</span>. — Декодер успешно восстанавливает как периодическую структуру, так и пространственную корреляцию спектральных пиков различной сложности, достоверно воспроизводя характерную полосатую структуру и диагональное затухание, что подтверждает его способность точно отражать вторые статистические моменты $S(\omega)$ .

Гибкое спектральное моделирование: за пределами стационарности

Стационарные функции ядра, несмотря на свою математическую удобность, часто демонстрируют ограниченные возможности при моделировании сложных реальных данных. Это связано с тем, что стационарность предполагает, что статистические свойства сигнала не меняются во времени или пространстве, что является упрощением для многих практических задач. В частности, стационарные ядра испытывают трудности с захватом нелинейных зависимостей и взаимодействий, характерных для сложных систем. Например, при анализе временных рядов, подверженных сезонности или трендам, применение стационарного ядра может привести к значительным ошибкам моделирования. Аналогично, в задачах обработки изображений, стационарные ядра не всегда способны адекватно описывать текстуры и паттерны, меняющиеся в зависимости от местоположения. $K(x, x') = f(x - x')$ — типичное представление стационарного ядра, подчёркивающее зависимость только от разности аргументов.

Функции спектральной смеси представляют собой расширение стационарных ядер, достигаемое путем комбинирования гауссовых функций в частотной области. Вместо использования единого гауссова ядра, спектральные смеси используют взвешенную сумму нескольких гауссовых ядер с различными параметрами $\mu_i$ и $\sigma_i$ . Такой подход позволяет более точно моделировать сложные данные, поскольку позволяет учитывать различные частотные компоненты и их соответствующие масштабы. Веса $w_i$ определяют вклад каждой гауссовой функции в общую функцию ядра. В результате, спектральные смеси обеспечивают большую гибкость по сравнению со стационарными ядрами, позволяя адаптироваться к данным с более сложной спектральной структурой.

Аддитивные модели Гауссовских процессов повышают гибкость моделирования за счёт суммирования отдельных Гауссовских процессов по различным измерениям. Этот подход позволяет улавливать сложные взаимодействия между признаками, которые не могут быть эффективно представлены одним Гауссовским процессом. Вместо моделирования данных как функции от одного входного вектора, аддитивная модель рассматривает функцию как сумму функций, каждая из которых зависит от подмножества входных признаков. Математически, это можно представить как $f(x) = \sum_{i=1}^{d} f_i(x_i)$ , где $f_i$ — отдельный Гауссовский процесс, зависящий от $i$ -го измерения входного вектора $x$ . Такая декомпозиция позволяет моделировать нелинейные эффекты и взаимодействия между признаками более точно, чем традиционные стационарные ядра.

Модель точно восстанавливает спектральную плотность, корректно определяя положение пиков и ширину полосы для смесей различной сложности (от 1 до 4 компонент), что подтверждается совпадением истинных значений (синяя линия) и восстановленных данных (красная пунктирная линия) на графике, где по оси абсцисс отложена частота ω (Гц), а по оси ординат - величина спектральной плотности <span class="katex-eq" data-katex-display="false"> S(\omega) </span>. — Модель точно восстанавливает спектральную плотность, корректно определяя положение пиков и ширину полосы для смесей различной сложности (от 1 до 4 компонент), что подтверждается совпадением истинных значений (синяя линия) и восстановленных данных (красная пунктирная линия) на графике, где по оси абсцисс отложена частота ω (Гц), а по оси ординат — величина спектральной плотности $S(\omega)$ .

Декодирование спектральных представлений для эффективного вывода

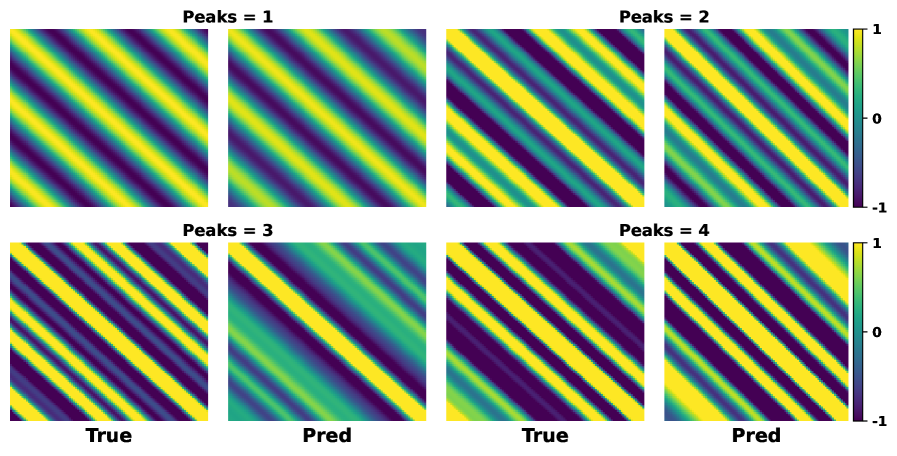
Декодер на основе фильтр-банка извлекает явные спектральные плотности из замороженных нейронных сетей, открывая возможности для интерпретируемых и эффективных предсказаний. Вместо работы с абстрактными латентными представлениями, данный подход позволяет напрямую анализировать частотные характеристики, которые сеть использует для принятия решений. Это достигается путем разложения скрытых слоёв на набор фильтров, каждый из которых соответствует определённой частоте или паттерну. Извлечённые спектральные плотности не только облегчают понимание логики работы сети, но и позволяют значительно ускорить процесс инференса, поскольку вычисления могут быть выполнены непосредственно в спектральной области, избегая дорогостоящих матричных операций, характерных для традиционных методов. Такая возможность особенно важна для развёртывания сложных моделей на устройствах с ограниченными вычислительными ресурсами, где эффективность играет ключевую роль.

Декодер, используемый в данной работе, эффективно извлекает скрытые представления посредством механизма Multi-Query Attention. Этот подход позволяет значительно снизить вычислительную нагрузку, поскольку вместо вычисления внимания для каждой пары запрос-ключ, используется общий набор ключей и значений для всех запросов. Такая оптимизация существенно уменьшает количество необходимых операций, особенно при работе с большими объёмами данных, сохраняя при этом способность модели улавливать важные взаимосвязи в данных. Благодаря этому, декодер способен быстро и эффективно обрабатывать информацию, делая его перспективным решением для задач, требующих высокой скорости и эффективности вычислений.

В основе предложенного подхода лежит структурное соответствие между Механизмом Внимания с Разделёнными Значениями и правилом обновления Гауссовского процесса. Данное соответствие позволяет не только углубить теоретическое понимание работы нейронных сетей, но и перенести преимущества Гауссовских процессов — такие как эффективное управление неопределённостью и возможность аналитического расчёта — в область глубокого обучения. По сути, механизм внимания имитирует процесс обновления апостериорного распределения в Гауссовском процессе, позволяя модели более эффективно обобщать данные и делать прогнозы, основанные на вероятностной оценке. Это обеспечивает не только повышенную точность, но и возможность интерпретации решений модели, поскольку они напрямую связаны с математической структурой Гауссовского процесса и его параметрами. $p(y|x,D) = \in t p(y|x,f) p(f|D) df$

Разработанная система демонстрирует значительное ускорение процесса вывода — примерно на три порядка величины — по сравнению с методами оптимизации ядер, такими как DKL и RFF. Несмотря на столь существенное повышение скорости, производительность системы остаётся сопоставимой с оптимизированными гауссовскими процессами, что подтверждено результатами тестов на эталонном наборе Kernel Cookbook. Такое сочетание скорости и точности делает данный подход особенно привлекательным для задач, требующих эффективной обработки больших объёмов данных и быстрых предсказаний, открывая новые возможности для применения в различных областях, от машинного обучения до анализа данных.

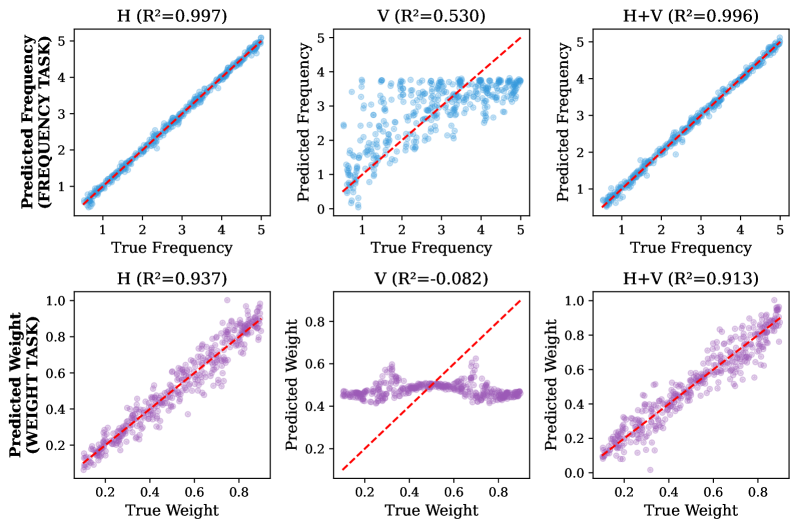
Визуализация t-SNE показывает, что представления PFN отражают спектральную структуру входного сигнала (ρ=0.86), при этом компоненты V демонстрируют частичную структуру (ρ=0.19), а K и Q, получаемые из <span class="katex-eq" data-katex-display="false">\phi_{x}</span>, не содержат информации о частоте и образуют скопления без корреляции с входным сигналом. — Визуализация t-SNE показывает, что представления PFN отражают спектральную структуру входного сигнала (ρ=0.86), при этом компоненты V демонстрируют частичную структуру (ρ=0.19), а K и Q, получаемые из $\phi_{x}$ , не содержат информации о частоте и образуют скопления без корреляции с входным сигналом.

Требования к данным и пределы идентифицируемости

В условиях ограниченного количества данных, так называемом пределе одной реализации, статистическая идентифицируемость существенно снижается, что создаёт значительные трудности при точной оценке спектральных характеристик. Это связано с тем, что при наличии лишь одного набора наблюдений, становится сложно однозначно определить истинный спектр, поскольку различные спектральные модели могут давать схожие результаты для данного набора данных. Вследствие этого, оценка спектральной плотности становится неустойчивой и подверженной значительным ошибкам, что ограничивает применимость спектральных моделей в задачах, где доступно лишь ограниченное количество наблюдений. Повышение точности оценки в таких условиях требует разработки специальных методов, способных эффективно справляться с проблемой недостатка данных и повышать устойчивость оценки спектральной плотности.

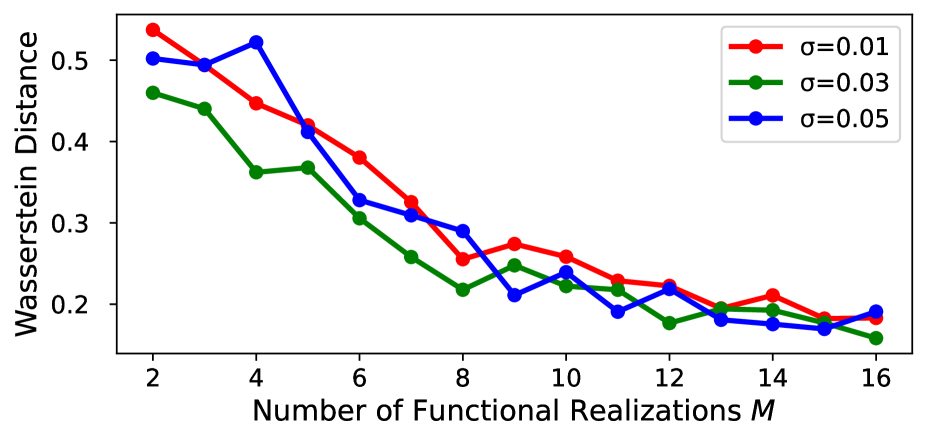
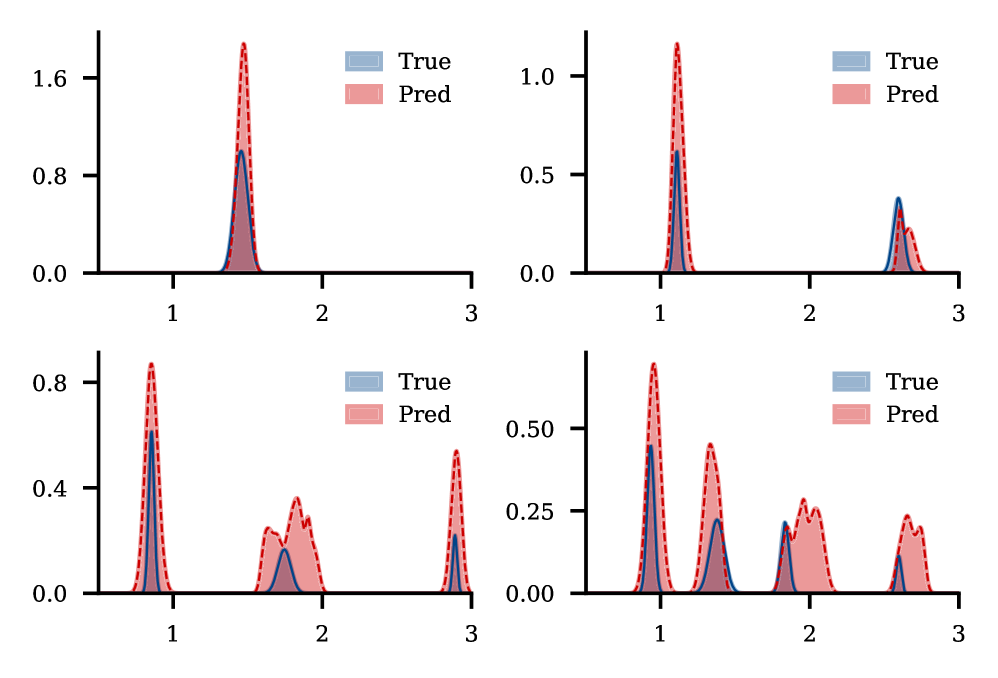
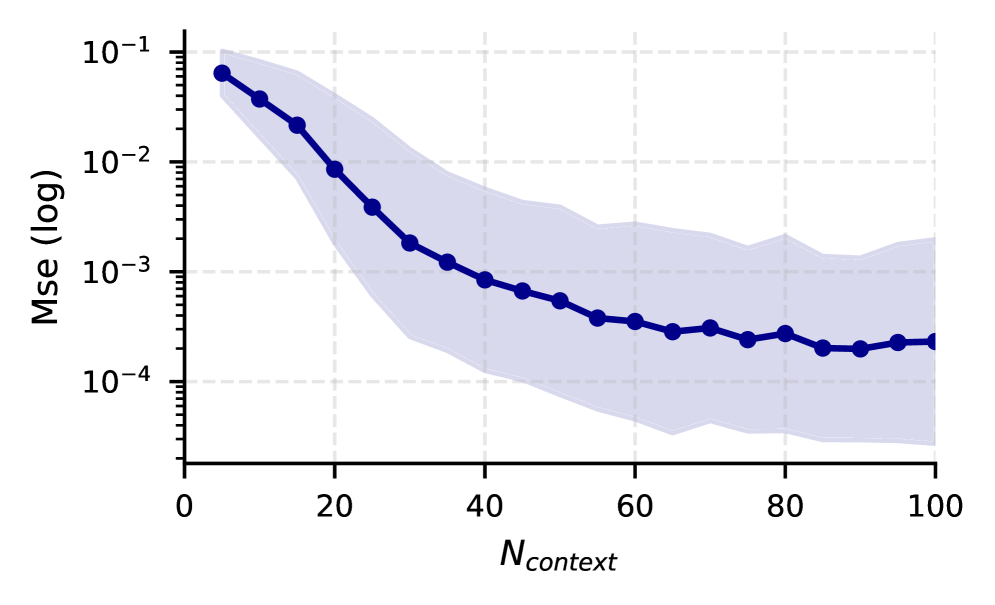
Исследования показывают, что существенное повышение точности и надёжности в задачах спектральной оценки достигается при переходе к многореализационному подходу. В отличие от сценария с единственным наблюдением, где статистическая идентифицируемость ограничена, использование множества независимых наблюдений позволяет значительно улучшить определение спектральных характеристик. Такой подход обеспечивает более устойчивые результаты, снижая влияние случайных колебаний и повышая достоверность полученных моделей. Это особенно важно в сложных системах, где точное определение спектральных свойств критически важно для дальнейшего анализа и прогнозирования. Увеличение количества независимых наблюдений ведёт к более надёжной оценке, приближаясь к истинному спектральному распределению и минимизируя погрешности, что подтверждается снижением расстояния Вассерштейна между истинной и предсказанной плотностями.

Разработанная методика демонстрирует высокую точность регрессии Гауссовых процессов, сопоставимую с результатами, полученными идеальной моделью — так называемым “Оракулом”. В частности, среднеквадратичная ошибка (MSE) регрессии приближается к значениям, достигаемым “Оракулом”, даже в десятимерных пространствах данных. При этом, производительность сохраняется на уровне 90-85% от оптимальной точности “Оракула”, что подтверждает эффективность подхода и его применимость к задачам анализа данных высокой размерности.

Исследования показали, что расстояние Вассерштейна между истинной и предсказанной спектральными плотностями неуклонно уменьшается с увеличением числа выборок Гауссовского процесса (GP). Данная закономерность демонстрирует, что предсказанные спектральные плотности сходятся к истинной спектральной плотности по мере накопления данных. Уменьшение расстояния Вассерштейна, являющегося метрикой, чувствительной к различиям в форме распределений, подтверждает, что модель GP способна всё точнее аппроксимировать истинное распределение данных с увеличением объёма выборки.

Перспективные исследования направлены на разработку методов устойчивой спектральной оценки в условиях ограниченного объёма данных. Несмотря на значительные успехи в моделировании с использованием гауссовских процессов, точность и надёжность этих моделей снижаются при недостатке наблюдений. Разработка алгоритмов, способных эффективно извлекать информацию из скудных данных, позволит расширить сферу применения спектральных моделей в различных областях, от анализа сигналов и изображений до моделирования сложных систем. Особое внимание уделяется методам, использующим априорные знания, регуляризацию и байесовский подход для повышения устойчивости и точности спектральной оценки в условиях дефицита данных, что открывает возможности для более глубокого понимания и прогнозирования поведения сложных систем.

Эксперименты показывают, что декодер с единичной реализацией обеспечивает высокую производительность при обработке данных.

Исследование демонстрирует, как из сложной сети, обученной на данных, можно извлечь явное спектральное ядро. Это напоминает попытку придать форму хаосу, выявить закономерности в кажущейся случайности. Как будто пытаешься понять, что заставляет систему работать, а не просто наблюдать за результатом. И в этом есть своя ирония, ведь, как однажды заметил Дональд Дэвис: «Любая абстракция умирает от продакшена». Однако, в данном случае, смерть абстракции — это не провал, а возможность построить более осмысленную и интерпретируемую модель, способную не только предсказывать, но и объяснять.

Что дальше?

Представленный подход к извлечению спектральных ядер из сетей, обученных с использованием априорных данных (PFN), безусловно, элегантен. Однако, как показывает опыт, каждая «революционная» технология завтра станет техническим долгом. Проблема интерпретируемости, хоть и смягчена, не решена полностью. В конечном счете, это просто еще один способ представить сложные данные в виде матрицы, которую кто-то должен будет отладить. И, судя по истории, отладка — это вечный процесс.

Следующим шагом, вероятно, станет попытка масштабирования этого метода на данные, которые не столь «удобны», как те, что использовались в эксперименте. А это значит — борьба с шумом, неполнотой данных и, конечно, с проклятием размерности. Не исключено, что «cloud-native» инфраструктура снова придет на помощь, позволяя переложить вычислительную нагрузку на плечи других, но это лишь отсрочит неизбежное. Мы ведь не код пишем — мы просто оставляем комментарии будущим археологам.

В конечном счете, истинный прогресс заключается не в создании новых алгоритмов, а в понимании того, почему они работают (или не работают). Если система стабильно падает, значит, она хотя бы последовательна. Поэтому, возможно, стоит сосредоточиться на разработке инструментов для диагностики и анализа этих систем, а не на бесконечной гонке за точностью.

Оригинал статьи: https://arxiv.org/pdf/2601.21731.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-31 00:33