Прогнозирование опционов CSI 300: глубокое обучение на волнах волатильности и настроениях рынка

Автор: Денис Аветисян

Новая модель, основанная на глубоком обучении, позволяет точнее оценивать стоимость опционов CSI 300, учитывая динамику волатильности и рыночные настроения.

🐢

Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.

Бесплатный Телеграм канал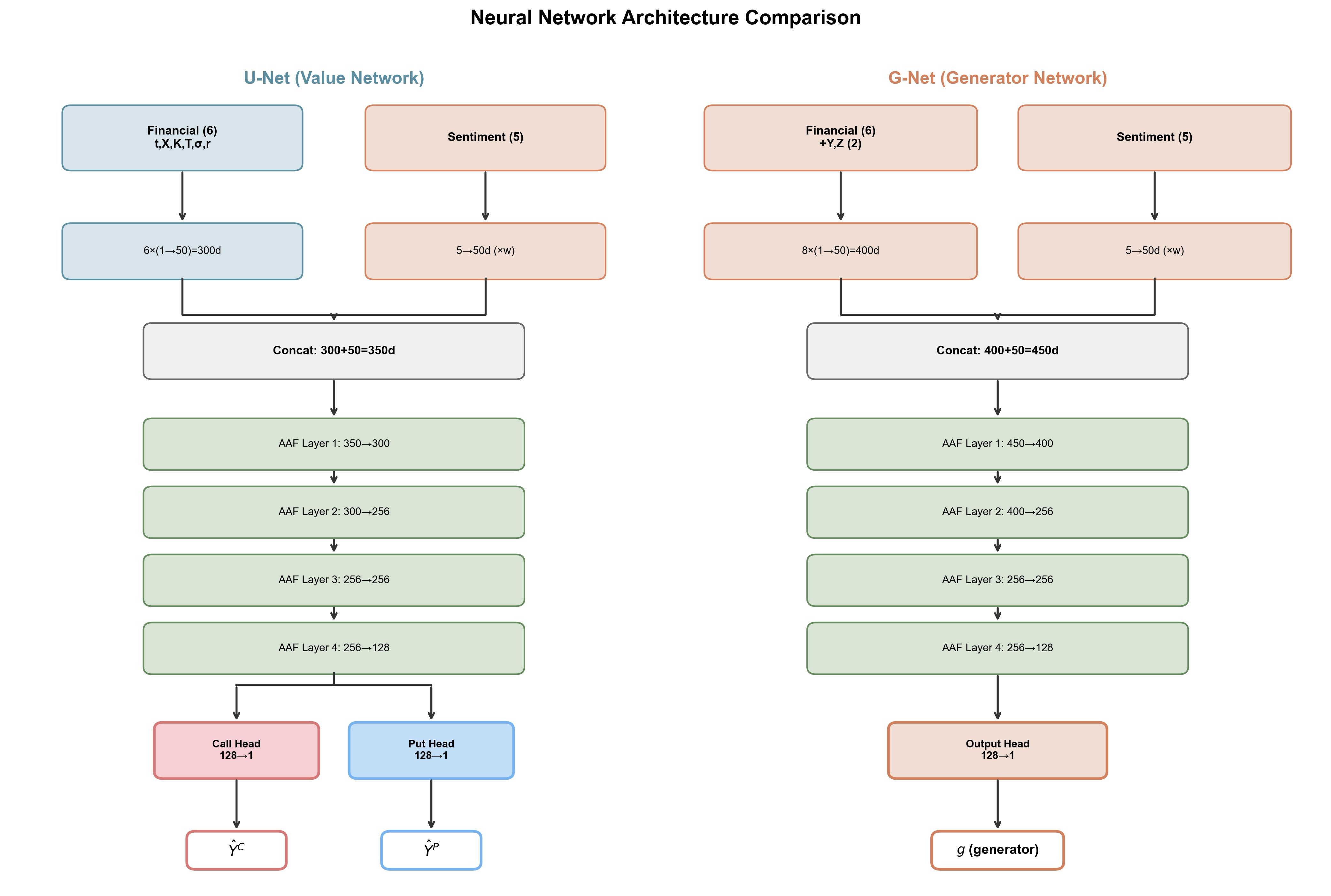

Архитектура сети оценки и генераторной сети демонстрирует общую основу с расширяющим финансовые переменные слоем и слоем встраивания признаков настроений, управляемым обучаемым параметром затвора, в то время как генераторная сеть, помимо этого, принимает на вход <span class="katex-eq" data-katex-display="false">Y_{t} </span> и <span class="katex-eq" data-katex-display="false">Z_{t} </span>, что позволяет моделировать взаимосвязь между финансовыми данными, настроениями и генерируемыми выходными данными. — Архитектура сети оценки и генераторной сети демонстрирует общую основу с расширяющим финансовые переменные слоем и слоем встраивания признаков настроений, управляемым обучаемым параметром затвора, в то время как генераторная сеть, помимо этого, принимает на вход $Y_{t}$ и $Z_{t}$ , что позволяет моделировать взаимосвязь между финансовыми данными, настроениями и генерируемыми выходными данными.

В работе предложена глубокая модель ценообразования опционов, использующая траектории волатильности и анализ рыночных настроений в рамках глубокой схемы FBSDE, что обеспечивает повышенную точность и интерпретируемость по сравнению с традиционными методами.

Традиционные модели ценообразования опционов, такие как модель Блэка-Шоулза-Мертона, часто сталкиваются с ограничениями из-за упрощающих предположений о постоянстве волатильности и отсутствии учета поведенческих факторов. В данной работе, посвященной ‘Deep g-Pricing for CSI 300 Index Options with Volatility Trajectories and Market Sentiment’, предложена новая методология, использующая глубокое обучение в рамках стохастических дифференциальных уравнений для более точной оценки опционов. Разработанная архитектура, учитывающая траектории волатильности и настроения рынка, позволяет снизить среднюю абсолютную ошибку на 32.2% и среднюю абсолютную процентную ошибку на 35.3% по сравнению с классической моделью. Возможно ли дальнейшее повышение интерпретируемости и эффективности модели за счет интеграции дополнительных источников информации и более сложных архитектур нейронных сетей?

Ограничения Традиционного Ценообразования Опционов

Классическая модель Блэка-Шоулза-Мертона, несмотря на широкое распространение в финансовом анализе, основывается на упрощающем предположении о постоянстве волатильности базового актива. В реальности, волатильность подвержена значительным колебаниям, обусловленным как рыночными факторами, так и макроэкономическими событиями. Это допущение о постоянстве существенно ограничивает точность модели в динамичных рыночных условиях, особенно при оценке опционов с длительным сроком действия или сложных производных финансовых инструментов. Постоянная волатильность не отражает наблюдаемые кластеры высокой и низкой волатильности, что приводит к систематическим ошибкам в ценообразовании и, как следствие, к потенциальным убыткам при использовании модели в практических приложениях.

Упрощение, связанное с предположением о постоянстве волатильности, зачастую приводит к неточной оценке опционов, особенно тех, у которых длительный срок до истечения или сложная структура выплат. Чем больше период до исполнения контракта, тем сильнее влияние даже незначительных погрешностей в оценке волатильности на конечную цену опциона. Опционы с экзотическими условиями, например, с барьерами или зависящие от нескольких базовых активов, требуют более точного учета динамики волатильности, поскольку стандартные модели, игнорирующие эту динамику, не способны адекватно отразить их стоимость. В результате, использование упрощенных моделей может привести к значительным финансовым потерям для инвесторов и искажению рыночных цен.

Точное отслеживание динамики волатильности имеет решающее значение для эффективного управления рисками и справедливой оценки опционов, что обуславливает потребность в более надежных моделях. Представленная методика направлена на преодоление ограничений, присущих традиционным подходам, и демонстрирует значительное улучшение точности. В ходе тестирования удалось добиться снижения средней абсолютной ошибки (MAE) на 32,2% по сравнению с базовой моделью Блэка-Шоулза-Мертона, что подтверждает эффективность разработанного подхода и его потенциал для применения в реальных финансовых условиях. Подобное улучшение позволяет более адекватно оценивать риски и принимать обоснованные инвестиционные решения.

Диаграммы рассеяния демонстрируют соответствие между предсказанными и фактическими значениями для различных уровней прибыльности.

FBSDE: Гибкий Фреймворк для Ценообразования

В отличие от традиционных моделей ценообразования опционов, основанных на строгих предположениях, фреймворк стохастических дифференциальных уравнений в прямом и обратном направлении (FBSDE) позволяет оценивать опционы при более широком спектре условий. Это достигается за счет отказа от необходимости предполагать, например, постоянную волатильность или отсутствие дивидендов. FBSDE использует стохастические процессы, описывающие эволюцию как цены базового актива, так и стоимости опциона, что позволяет моделировать более реалистичные рыночные сценарии и учитывать различные факторы, влияющие на цену опциона. Это особенно важно при работе со сложными опционами или в условиях неполных рынков, где традиционные модели могут давать неточные результаты.

Традиционные модели ценообразования опционов, такие как модель Блэка-Шоулза, опираются на ряд ограничивающих предположений, включая постоянную волатильность и отсутствие дивидендов. В отличие от них, фреймворк FBSDE позволяет отделить процесс оценки опциона от этих жестких ограничений. Это достигается за счет возможности непосредственного включения рыночной информации, такой как кривая волатильности, и использования стохастических моделей волатильности, учитывающих ее изменение во времени. В результате, оценка становится более точной и адаптивной к реальным рыночным условиям, что особенно важно при работе со сложными опционами и неликвидными активами.

В основе фреймворка FBSDE лежит архитектура двойной нейронной сети, которая одновременно оптимизирует оценку опциона и механизм ценообразования базового актива. Данный подход позволяет добиться снижения средней абсолютной процентной ошибки (MAPE) на 35.3% по сравнению с базовой моделью Блэка-Шоулза (BSM). Совместное обучение этих двух компонентов повышает точность оценки опционов и обеспечивает более адекватное отражение динамики рынка, что критически важно для сложных финансовых инструментов.

Использование Рыночных Сигналов для Повышения Точности

Интеграция реализованной волатильности и рыночных настроений в качестве входных признаков позволяет получить более детализированную и реалистичную оценку будущей волатильности. Реализованная волатильность, рассчитываемая на основе исторических данных о ценовых колебаниях, предоставляет объективную меру фактической волатильности актива. Дополнение этих данных показателями рыночных настроений, полученными из новостных лент, социальных сетей и других источников, позволяет учесть субъективные факторы, влияющие на поведение инвесторов и, следовательно, на будущую волатильность. Комбинирование этих двух типов данных обеспечивает более полное представление о рыночной динамике, что потенциально улучшает точность прогнозирования и оценки опционов.

Механизм адаптивного взвешивания сигналов, известный как Sentiment Gating, динамически определяет вклад отдельных входных данных — реализованной волатильности и рыночных настроений — в общую оценку будущей волатильности. В отличие от статических методов объединения, Sentiment Gating использует данные о производительности каждого сигнала для определения его текущей прогностической силы. Сигналы, демонстрирующие высокую корреляцию с будущими изменениями волатильности, получают больший вес, в то время как менее релевантные сигналы оказывают меньшее влияние на итоговую оценку. Такой адаптивный подход позволяет модели более эффективно использовать доступную информацию и повышает точность прогнозирования, особенно в условиях меняющейся рыночной динамики.

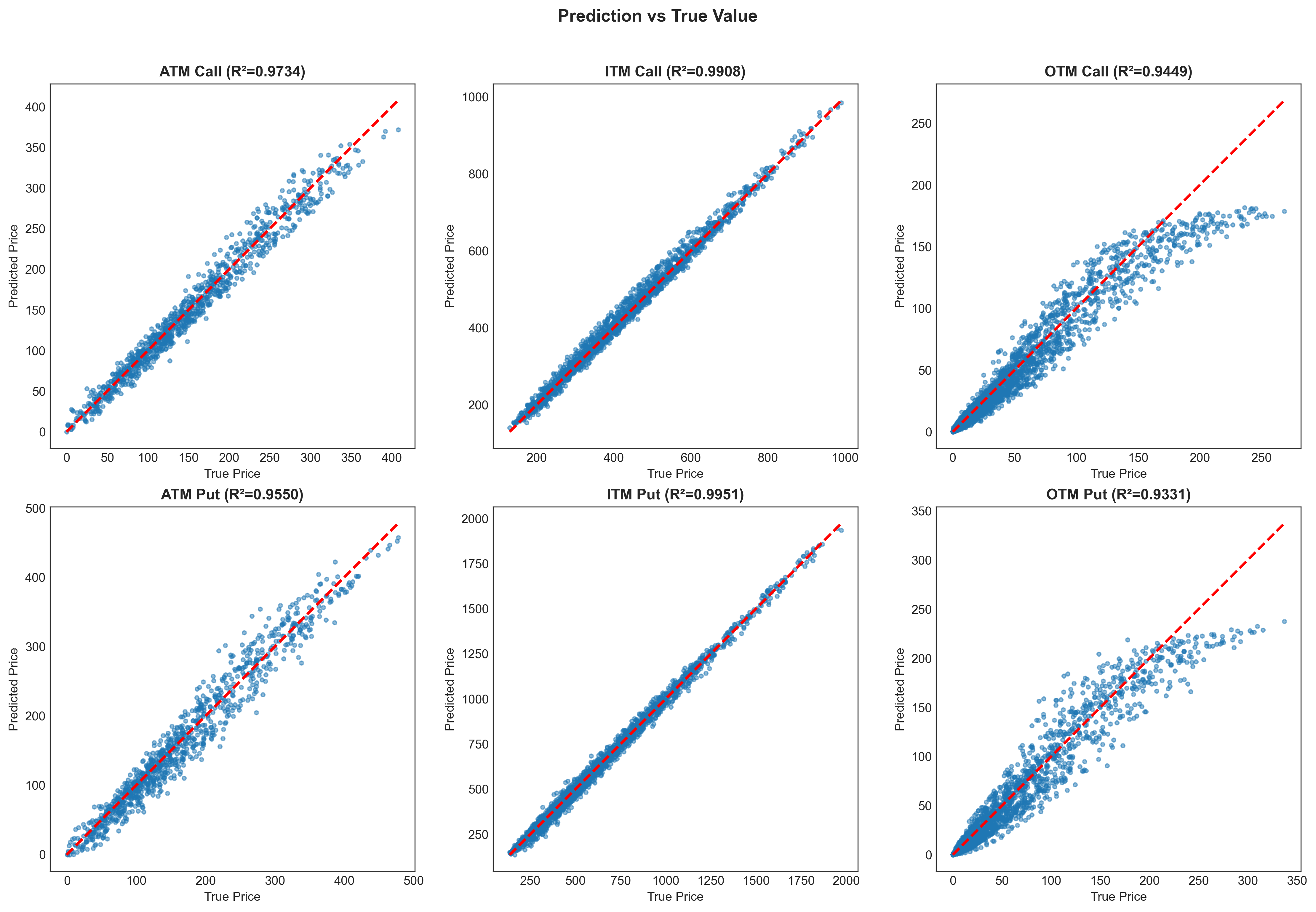
Использование траектории волатильности в качестве входных данных позволяет модели прогнозировать будущие паттерны волатильности, что приводит к более точным ценам опционов. В частности, данный подход позволил снизить частоту экстремальных ошибок (MAPE > 100%) с 11.51% до 0.77% для опционов, находящихся вне границ цен (Out-of-the-Money). Это значительное улучшение свидетельствует о повышенной способности модели корректно оценивать стоимость опционов в условиях высокой неопределенности и резких колебаний рынка.

Интерпретируемое Ценообразование Опционов с Использованием Искусственного Интеллекта

Использование методов интерпретируемости, таких как значения Шепли и интегрированные градиенты, позволяет раскрыть вклад каждого входного параметра в итоговую цену опциона. Эти методы, основанные на принципах теории игр и дифференциального исчисления, позволяют количественно оценить, насколько изменение конкретного фактора — например, цены базового актива, времени до экспирации или волатильности — влияет на предсказанную стоимость опциона. Анализ, основанный на значениях Шепли, выявляет средний вклад каждого параметра во все возможные комбинации входных данных, обеспечивая стабильную и надежную оценку важности признаков. Интегрированные градиенты, в свою очередь, позволяют проследить, как изменение каждого параметра влияет на выход модели, предоставляя информацию о направлении и силе влияния. В результате, становится возможным не только предсказывать цену опциона, но и понимать, какие факторы оказывают наибольшее влияние, что способствует более глубокому анализу рынка и принятию обоснованных инвестиционных решений.

Прозрачность, обеспечиваемая методами интерпретируемости, играет ключевую роль в укреплении доверия к моделям ценообразования опционов. Возможность отследить вклад каждого входного параметра позволяет выявить потенциальные смещения или ошибки в логике модели, которые могли бы привести к неверным оценкам. В частности, анализ с использованием методов, подобных значениям Шэпли и интегрированным градиентам, позволяет оценить, насколько сильно определенные факторы, такие как настроения рынка или траектория волатильности, влияют на конечную цену опциона. Такое понимание не только повышает уверенность в корректности модели, но и предоставляет ценную информацию для выявления и устранения систематических ошибок, что критически важно для принятия обоснованных инвестиционных решений и эффективного управления рисками.

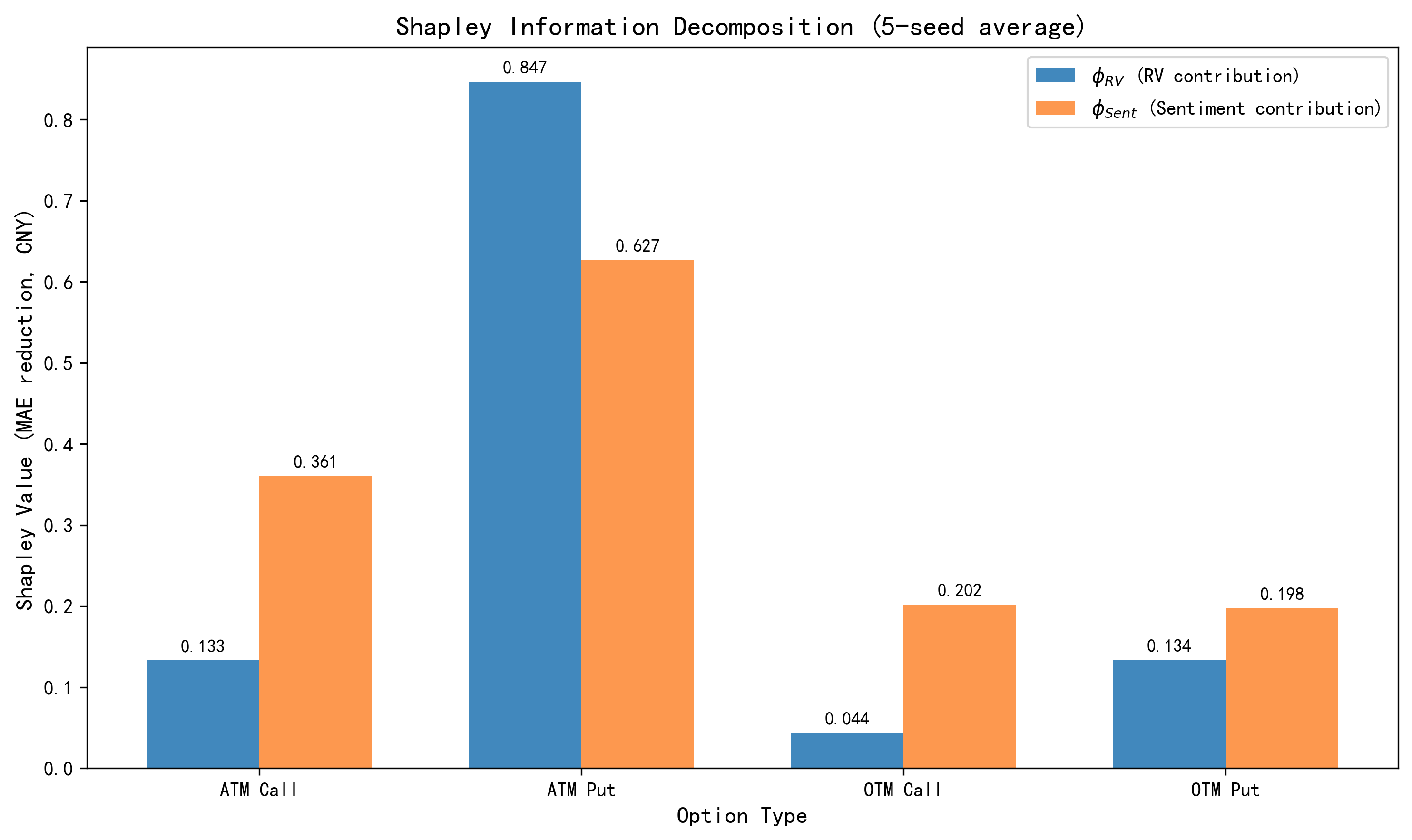
Понимание ключевых факторов, определяющих цены опционов, позволяет участникам рынка принимать более обоснованные решения и эффективно управлять рисками. Проведенный анализ выявил, что для опционов колл с ценой исполнения, равной текущей рыночной цене (ATM), рыночные настроения оказывают доминирующее влияние на прогноз цены, составляя 90,7%. В то же время, для опционов пут с ценой исполнения, равной текущей рыночной цене, определяющим фактором является траектория волатильности, вносящая 60,9% в конечную оценку. Данные результаты подчеркивают важность учета не только количественных показателей, но и качественных факторов, таких как общее настроение инвесторов, при формировании стратегий торговли опционами и оценке потенциальных рисков.

Разложение по значению Шепли позволяет оценить вклад каждого компонента в общую производительность системы.

Исследование демонстрирует, что попытки построения точных моделей ценообразования опционов сталкиваются с необходимостью учитывать не только волатильность, но и рыночные настроения. Авторы предлагают подход, основанный на глубоком обучении, который позволяет извлекать полезную информацию из траекторий волатильности и данных о настроениях инвесторов. Как однажды заметил Джон Локк: «Всякое знание есть, в сущности, знание причин». В данном случае, модель стремится выявить причинно-следственные связи между рыночными факторами и ценами опционов, что позволяет повысить точность прогнозов и обеспечить большую прозрачность процесса ценообразования, в отличие от традиционных, менее гибких методов.

Что дальше?

Представленная работа, безусловно, демонстрирует потенциал глубокого обучения в ценообразовании опционов. Однако, иллюзия точности, создаваемая сложными моделями, требует постоянного критического осмысления. Улучшение метрик — это лишь часть задачи; гораздо важнее — понимание природы возникающих ошибок. Истинную ценность имеет не столько предсказание цены, сколько оценка погрешности этого предсказания.

Перспективы дальнейших исследований лежат не только в усложнении архитектуры нейронных сетей, но и в интеграции с более фундаментальными моделями, учитывающими не только волатильность и настроения рынка, но и микроструктуру торгов, а также влияние макроэкономических факторов. Необходимо разработать методы, позволяющие выявлять и корректировать смещения, возникающие из-за неполноты или искажения данных.

В конечном счете, успех в этой области будет зависеть не от создания “черного ящика”, генерирующего точные числа, а от разработки прозрачной и интерпретируемой системы, позволяющей понимать, почему модель принимает те или иные решения. Иначе, рискуем вновь оказаться в ситуации, когда сложные алгоритмы лишь маскируют наше невежество.

Оригинал статьи: https://arxiv.org/pdf/2601.18804.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-28 13:47