Автор: Денис Аветисян
Исследователи предлагают использовать инструменты дифференциальной геометрии для анализа информационных потоков внутри нейронных сетей, открывая новые возможности для оптимизации и обрезки моделей.
Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.
Бесплатный Телеграм канал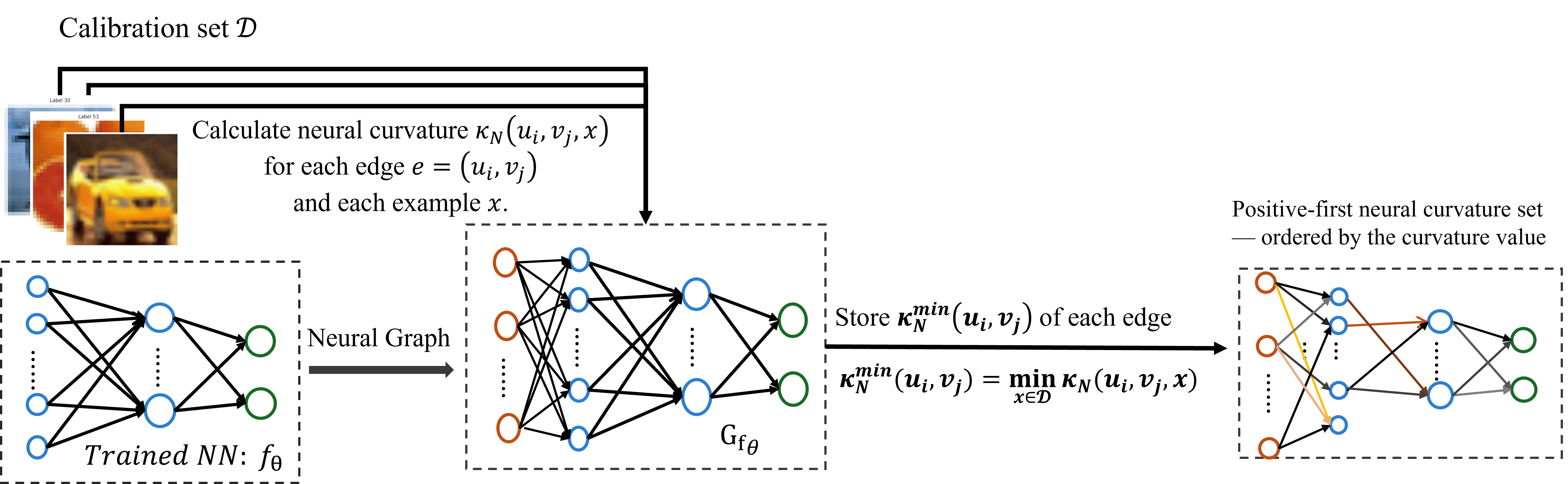
В статье представлен метод, основанный на теории графов и кривизне Риччи, для выявления критических связей и улучшения эффективности нейронных сетей.
Понимание потока информации в нейронных сетях, выявление наиболее значимых связей, остается сложной задачей. В работе ‘Analyzing Neural Network Information Flow Using Differential Geometry’ предложен новый подход к анализу этого потока, основанный на теории графов и дифференциальной геометрии, в частности, на понятии кривизны Олливье-Риччи. Показано, что вычисление кривизны позволяет ранжировать связи в сети по их важности, при этом связи с отрицательной кривизной являются критическими для функционирования модели, а положительные — менее значимыми. Может ли этот подход стать основой для более эффективных методов обрезки и анализа надежности нейронных сетей?
Нейронные сети: избыточность как неизбежный техдолг
Современные нейронные сети, несмотря на свою впечатляющую производительность, часто характеризуются избыточностью соединений. Это означает, что значительная часть параметров сети не вносит существенного вклада в конечный результат, являясь, по сути, резервными или дублирующими элементами. Избыточность напрямую влияет на вычислительные затраты и требования к памяти, что особенно критично при развертывании моделей на мобильных устройствах или в системах с ограниченными ресурсами. Каждое лишнее соединение требует дополнительных вычислений во время обучения и инференса, замедляя работу сети и увеличивая энергопотребление. Таким образом, выявление и устранение этих избыточных связей становится ключевой задачей для повышения эффективности и масштабируемости современных нейронных сетей.
Традиционные методы прореживания нейронных сетей, направленные на удаление неважных связей, часто сталкиваются с проблемой значительного снижения производительности. Попытки грубого удаления соединений, основанные на простых метриках, как правило, приводят к потере критически важной информации, необходимой для точной работы модели. Это особенно заметно в сложных архитектурах, где каждая связь может вносить свой вклад в общую функциональность. В результате, сети, подвергшиеся подобной прореживании, демонстрируют заметное ухудшение точности, что делает их непригодными для практического применения. Эффективное выявление и удаление избыточных параметров без ущерба для качества предсказаний остается сложной задачей, требующей разработки более интеллектуальных и адаптивных подходов к прореживанию.
Разработка интеллектуальных методов обрезки нейронных сетей становится критически важной задачей в связи с растущей потребностью в развертывании искусственного интеллекта на устройствах с ограниченными ресурсами. Традиционные подходы к сокращению числа параметров зачастую приводят к существенной потере точности, что делает их непригодными для практического применения. Новые алгоритмы, способные избирательно удалять наименее значимые связи, сохраняя при этом ключевую информацию, позволяют значительно уменьшить размер модели и вычислительные затраты без ущерба для производительности. Это особенно важно для мобильных устройств, встроенных систем и других платформ, где энергоэффективность и скорость обработки данных имеют первостепенное значение. В результате, более компактные и эффективные нейронные сети открывают возможности для широкого внедрения искусственного интеллекта в повседневную жизнь.
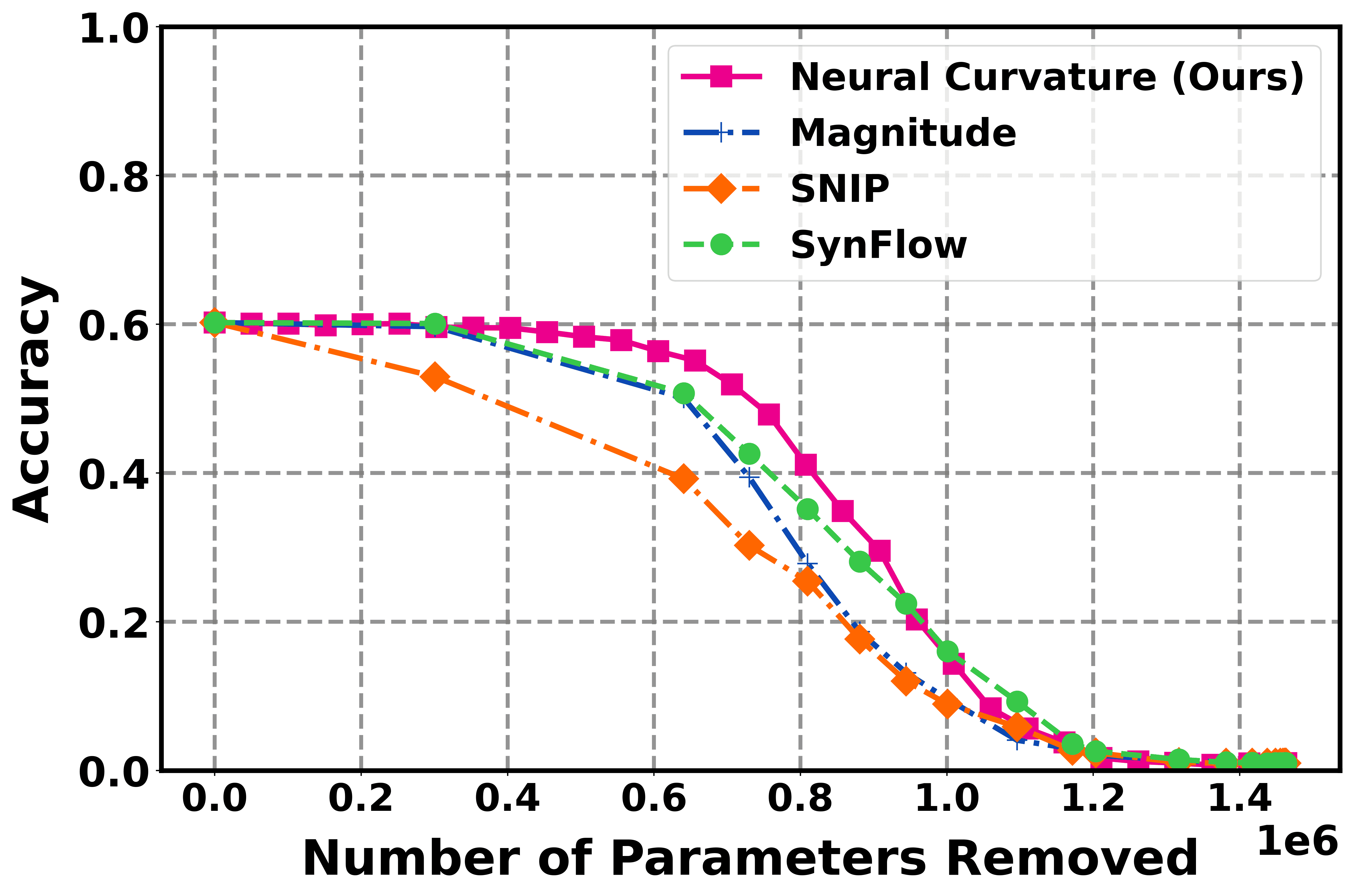
Существующие методы прореживания: ландшафт подходов
Метод обрезки на основе величины весов отличается простотой реализации, однако часто приводит к удалению критически важных связей в нейронной сети. Этот подход основывается исключительно на абсолютной величине весов, игнорируя их функциональную значимость и вклад в общую производительность модели. В результате, даже небольшие по величине веса, участвующие в важных вычислениях, могут быть удалены, что негативно сказывается на точности и обобщающей способности сети. Отсутствие учета функционального значения веса является основным недостатком данного метода по сравнению с более сложными подходами.
Методы, такие как SNIP и SynFlow, стремятся улучшить процесс прунинга, учитывая чувствительность функции потерь к удалению отдельных параметров. В отличие от прунинга на основе величины весов, которые удаляют параметры исключительно по их размеру, SNIP и SynFlow оценивают влияние каждого параметра на изменение функции потерь. Это достигается путем вычисления градиента функции потерь по отношению к каждому параметру, что позволяет определить, какие параметры оказывают наибольшее влияние на точность модели. Удаление параметров с наименьшей чувствительностью к функции потерь позволяет сохранить наиболее важные соединения и минимизировать снижение производительности после прунинга. Таким образом, SNIP и SynFlow обеспечивают более обоснованный и эффективный процесс прунинга по сравнению с более простыми подходами.
Несмотря на улучшения по сравнению с прунингом на основе величины весов, методы, такие как SNIP и SynFlow, по-прежнему используют приближения первого порядка для оценки важности нейронов. Это означает, что при вычислении влияния удаления конкретного соединения учитывается только линейная зависимость между изменением веса и изменением функции потерь. Такой подход может быть недостаточным для точной оценки в сложных нейронных сетях, где взаимодействия между нейронами носят нелинейный характер. В результате, важные для функционирования сети связи могут быть ошибочно удалены, так как их вклад в функцию потерь не будет учтен в полной мере при использовании только первого порядка приближения.

Нейронные сети как графы: новый взгляд на проблему
Рассмотрение нейронных сетей как графов позволяет применять инструменты теории графов для анализа связности сети и потока информации. В данном контексте, узлы графа представляют собой нейроны, а ребра — соединения между ними. Использование таких инструментов, как матрицы смежности и матрицы инцидентности, дает возможность количественно оценить структуру сети, определить центральность нейронов и выявить узкие места в потоке данных. Анализ связности позволяет определить, насколько устойчива сеть к повреждениям и как информация распространяется между нейронами. Кроме того, методы теории графов позволяют выявить кластеры нейронов, выполняющих схожие функции, что способствует лучшему пониманию архитектуры сети и ее способности к обобщению. Данный подход особенно полезен при анализе больших и сложных нейронных сетей, где традиционные методы анализа могут быть недостаточно эффективными.
В контексте представления нейронных сетей в виде графов, понятие Риччи-кривизны, заимствованное из дифференциальной геометрии, позволяет численно оценить значимость отдельных ребер (связей) в сети. Изначально определяемая для римановых многообразий, Риччи-кривизна адаптируется для графов путем рассмотрения локальной структуры соседних узлов. K(i) = \sum_{j \in N(i)} (d(i) - d(j)), где N(i) — множество соседей узла i, а d(i) — степень узла i. Отрицательные значения Риччи-кривизны указывают на ребра, критичные для поддержания связности и потока информации, поскольку их удаление может привести к фрагментации графа и ухудшению производительности сети. Положительные значения, напротив, указывают на избыточные связи, удаление которых может незначительно повлиять на общую функциональность.
Определение ребер с низкой кривизной Риччи позволяет выявлять критически важные соединения, обеспечивающие поддержание потока данных и функциональности нейронной сети. Низкое значение кривизны указывает на значительное влияние данного ребра на общую связность графа и, следовательно, на его роль в передаче информации. Идентифицируя такие ребра, можно оценить устойчивость сети к удалению соединений и определить узкие места, ограничивающие пропускную способность. \text{Кривизна Риччи} = R является мерой того, как локальная геометрия графа влияет на поток информации, и низкие значения указывают на ключевые связи для сохранения глобальной функциональности.

Количественная оценка важности: нейронная кривизна на практике
Вычисление риччиевского искривления напрямую требует значительных вычислительных ресурсов, что делает его непрактичным для анализа больших нейронных сетей. В связи с этим, для оценки искривления в контексте нейронных сетей используется аппроксимация Олливье-Риччи. Данный метод представляет собой дискретное приближение, основанное на анализе локальной геометрии данных и позволяет эффективно оценивать искривление для каждого соединения в сети, предоставляя возможность ранжировать их по значимости без чрезмерных вычислительных затрат. В отличие от точного вычисления, аппроксимация Олливье-Риччи оперирует с дискретными данными, что значительно снижает сложность вычислений.
Аппроксимация кривизны Олливье-Риччи основана на принципах теории информации и использует расстояние Вассерштейна для оценки расстояния между распределениями вероятностей. Расстояние Вассерштейна, также известное как расстояние Землекопа, определяет минимальную «стоимость» перемещения одной вероятностной массы в другую. В контексте нейронных сетей, распределения вероятностей формируются на основе активаций нейронов в локальных окрестностях. Вычисление расстояния Вассерштейна позволяет оценить, насколько сильно изменяется выходное распределение при небольшом изменении входных данных, что является ключевым аспектом при определении кривизны и, следовательно, важности связей в сети. W(P, Q) = \in f_{γ ∈ Π(P, Q)} E_{(x, y) \sim γ}[||x - y||], где Π(P, Q) — множество всех совместных распределений вероятностей, имеющих P и Q в качестве маргинальных распределений.
Комбинируя методы аппроксимации кривизны Олливье-Риччи с концепциями теории информации и расстоянием Вассерштейна, возможно эффективно вычислить показатель «кривизны нейронной сети» для каждой связи в сети. Этот показатель, представляющий собой скалярное значение, отражает локальную геометрию пространства параметров, определяемую распределением активаций и весов. Вычисление производится путем оценки расстояния Вассерштейна между эмпирическими распределениями активаций, полученными при небольших возмущениях входных данных. Затем, полученные значения используются для ранжирования связей по степени их важности: более низкие значения кривизны указывают на более важные связи, в то время как высокие значения могут свидетельствовать о избыточности или неэффективности. Данный подход позволяет идентифицировать критически важные соединения, которые оказывают наибольшее влияние на поведение сети и, следовательно, могут быть использованы для оптимизации архитектуры или сжатия модели.

За пределами эффективности: последствия и будущие направления
Применение метода обрезки, основанного на кривизне нейронной сети, к таким наборам данных, как MNIST, CIFAR-10 и CIFAR-100, продемонстрировало существенное сжатие моделей при минимальной потере точности. Эксперименты показали, что данный подход обеспечивает результаты, сопоставимые или превосходящие современные методы обрезки, позволяя значительно уменьшить размер моделей без существенного ухудшения их производительности. Особенно примечательно, что полученные модели сохраняют высокую точность даже после значительного сокращения числа параметров, что открывает новые возможности для развертывания глубокого обучения на устройствах с ограниченными ресурсами и в приложениях, требующих высокой скорости обработки данных. Такой подход позволяет не только оптимизировать существующие архитектуры, но и служит основой для разработки более эффективных и компактных моделей будущего.
Предложенный метод, основанный на анализе кривизны нейронной сети, обеспечивает принципиально новый подход к выявлению и удалению избыточных связей. В отличие от традиционных методов, полагающихся на эмпирические правила или случайный отбор, данный подход использует математическую основу для оценки вклада каждой связи в общую функцию сети. Это позволяет целенаправленно удалять наименее значимые соединения, существенно уменьшая размер модели без значительной потери точности. В результате получаются более компактные и эффективные модели, пригодные для развертывания на устройствах с ограниченными ресурсами, таких как мобильные телефоны или встроенные системы, и способные к более быстрой обработке данных.
Исследования показали, что предложенный метод обрезки нейронных сетей отличается высокой эффективностью при использовании ограниченного объема данных для калибровки. В частности, удалось добиться существенного сжатия моделей, удаляя избыточные связи, всего лишь с десятью обучающими примерами на каждую категорию. Такая способность к обучению на небольшом наборе данных открывает возможности для применения данной техники в условиях ограниченных ресурсов, где сбор и аннотация большого количества данных является затруднительным или невозможным. Это особенно актуально для задач, связанных с обработкой редких или специализированных данных, где получение большого набора примеров представляет значительную сложность.
Исследования в области применения анализа кривизны нейронных сетей планируют расширить горизонты за пределы текущих архитектур и задач. Предполагается, что данный подход позволит не только оптимизировать существующие модели, но и открыть возможности для создания принципиально новых, более эффективных алгоритмов глубокого обучения. В частности, особое внимание будет уделено применению к сложным задачам, требующим обработки больших объемов данных и высокой точности, таким как обработка естественного языка и компьютерное зрение. Ожидается, что дальнейшее развитие данной методики приведет к значительному снижению вычислительных затрат и энергопотребления, что особенно важно для развертывания моделей на мобильных устройствах и в системах с ограниченными ресурсами. Перспективы включают автоматизированный поиск оптимальных конфигураций нейронных сетей, адаптированных к конкретным задачам и аппаратным платформам, что позволит добиться существенного прогресса в области искусственного интеллекта.

Исследование потоков данных в нейронных сетях с помощью дифференциальной геометрии — занятная затея. Авторы пытаются применить серьёзный математический аппарат к области, где, будем честны, часто выживает сильнейший, а не самый элегантный. Анализ кривизны Риччи для определения критических связей — это как пытаться измерить хаос линейкой. Впрочем, если это поможет более эффективно обрезать ненужные соединения, то, возможно, и не такая уж и бессмысленная трата времени. Как сказал Андрей Колмогоров: «Математика — это искусство находить закономерности там, где их, казалось бы, нет». И в данном случае, закономерности эти ищутся в кажущемся хаосе весов нейронной сети.
Куда же это всё ведёт?
Предложенный анализ потоков данных в нейронных сетях посредством дифференциальной геометрии, безусловно, элегантен. Однако, как известно каждому, кто видел смерть идеальных диаграмм, любая абстракция рано или поздно умирает от продакшена. Выявление критических связей на основе кривизны Риччи — это хорошо, но стоит помнить: всё, что можно задеплоить — однажды упадёт. Вопрос не в том, чтобы найти идеальную сеть, а в том, как быстро и изящно она сломается.
Очевидным направлением является расширение применения этого подхода к более сложным архитектурам, таким как трансформеры, где графовое представление данных становится ещё более размытым. Впрочем, и здесь, вероятно, возникнут сложности с интерпретацией результатов, а упрощения неизбежно приведут к потере информации. CI/CD — это просто новый вид паники, только с графиками, и эта паника никуда не денется.
В конечном итоге, ценность этого исследования, скорее всего, будет заключаться не в создании принципиально новых алгоритмов обрезки, а в углублении понимания того, как информация течёт внутри чёрного ящика. И пусть этот поток окажется хаотичным и непредсказуемым, зато красиво умирает.
Оригинал статьи: https://arxiv.org/pdf/2601.16366.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- БИТКОИН ПРОГНОЗ. BTC криптовалюта
- ПРОГНОЗ ДОЛЛАРА К ШЕКЕЛЮ
- SOL ПРОГНОЗ. SOL криптовалюта
- ЭФИРИУМ ПРОГНОЗ. ETH криптовалюта
- SAROS ПРОГНОЗ. SAROS криптовалюта
- AXS ПРОГНОЗ. AXS криптовалюта
- FARTCOIN ПРОГНОЗ. FARTCOIN криптовалюта
- РИППЛ ПРОГНОЗ. XRP криптовалюта
- ДОГЕКОИН ПРОГНОЗ. DOGE криптовалюта
- ПРОГНОЗ ЕВРО К ШЕКЕЛЮ
2026-01-26 16:17