Раскрывая структуру связей: новый подход к идентификации графов

Автор: Денис Аветисян

В статье представлен инновационный метод анализа графов, позволяющий восстановить структуру сети по наблюдаемым данным.

График, реконструированный посредством метода, описанного в работе [3], демонстрирует возможность восстановления данных, намекая на то, что даже из хаоса можно выудить структуру, если подобрать правильное «заклинание».

Предлагается фреймворк сопоставления ковариаций для идентификации топологии графов с использованием римановой оптимизации и структурного моделирования.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал

Идентификация топологии графа, критически важная задача в анализе сетевых систем, часто осложняется скрытой структурой и доступностью лишь узловых данных. В работе, озаглавленной ‘Graph Topology Identification Based on Covariance Matching’, предложен новый подход, основанный на сопоставлении ковариационных матриц, позволяющий напрямую связать эмпирическую ковариацию наблюдаемых данных с теоретической ковариацией, подразумеваемой базовым графом. Показано, что предложенный метод CovMatch обеспечивает унифицированный путь к восстановлению структуры графа, если процесс генерации данных допускает явное выражение ковариации, и эффективно работает как для неориентированных, так и для разреженных ориентированных графов. Не откроет ли это подход новые возможности для обучения сложным сетевым топологиям с минимальными предположениями и превзойдет ли существующие методы, такие как логарифмический детерминант или байесовские подходы?

Раскрытие связей: Ковариация как ключ к пониманию данных

Во многих задачах анализа данных ключевым является понимание взаимосвязей между различными переменными. Эти связи часто количественно оцениваются с помощью ковариационной матрицы Σ, которая отражает, как переменные изменяются вместе. По сути, ковариация измеряет степень, в которой две переменные связаны линейно — положительная ковариация указывает на тенденцию обеих переменных увеличиваться или уменьшаться одновременно, отрицательная — на противоположное поведение. Изучение ковариационной матрицы позволяет выявить скрытые зависимости, что критически важно для построения эффективных моделей прогнозирования, кластеризации данных и, в конечном итоге, для извлечения ценной информации из сложных наборов данных. Оценка этих взаимосвязей является фундаментальным шагом в широком спектре приложений, от финансовых рынков и генетики до обработки изображений и нейронных сетей.

Традиционные статистические методы, такие как корреляционный анализ и регрессия, часто демонстрируют снижение эффективности при работе с данными высокой размерности. Это связано с тем, что количество параметров, необходимых для описания взаимосвязей между переменными, растёт экспоненциально с увеличением числа переменных. В результате, оценка $CovarianceMatrix$ становится нестабильной и подверженной ошибкам, что затрудняет выявление истинных зависимостей и приводит к неточным выводам. Проблема усугубляется эффектом «проклятия размерности», когда разреженность данных снижает статистическую значимость результатов и требует всё большего объёма данных для достижения сопоставимой точности. Вследствие этого, классические подходы оказываются недостаточно эффективными для анализа сложных систем, характеризующихся большим количеством взаимосвязанных переменных, что стимулирует развитие новых методов, специально предназначенных для работы с данными высокой размерности.

Эффективная оценка графа связей между переменными играет ключевую роль в моделировании сложных взаимодействий, однако представляет собой серьезную вычислительную задачу. Попытки реконструировать эти связи из данных часто приводят к значительным ошибкам, особенно при работе с высокоразмерными наборами данных. Причина кроется в том, что алгоритмы сталкиваются с экспоненциальным ростом сложности по мере увеличения числа переменных и связей, что приводит к неточным или неполным графам. Точность восстановления структуры графа напрямую влияет на качество последующего анализа и интерпретации данных, поэтому разработка более эффективных и масштабируемых методов оценки графа остается актуальной задачей в области анализа данных и машинного обучения. Например, при исследовании генетических сетей или социальных взаимодействий, неточности в оценке графа могут привести к ошибочным выводам о ключевых регуляторах или влиятельных узлах.

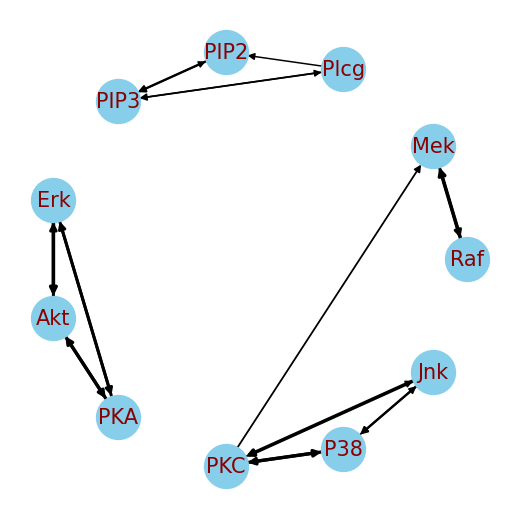
Предложенный подход позволяет получить оценку консенсусной сети, сопоставимую с эталонной.

Спектральные шаблоны: Оценка графов на основе ковариации

Метод SpecTemp представляет собой новый подход к оценке структуры графа, основанный на анализе спектральных свойств матрицы ковариации. В отличие от традиционных методов, которые опираются на прямую оценку смежности или расстояний между узлами, SpecTemp использует собственные значения и собственные векторы матрицы ковариации Σ для реконструкции связей в графе. Этот подход позволяет извлекать информацию о структуре графа из данных, представленных в виде ковариационной матрицы, что особенно полезно в сценариях, где прямые измерения связей недоступны или зашумлены. Анализ спектральных свойств позволяет идентифицировать кластеры и связи между узлами, не требуя явного построения матрицы смежности, что обеспечивает вычислительную эффективность и устойчивость к шуму.

Метод SpecTemp эффективно извлекает информацию из матрицы ковариации данных, обеспечивая надежную основу для построения графа. Анализ ковариации позволяет точно определить связи между переменными и, следовательно, структуру графа. В ходе экспериментов продемонстрирована высокая точность реконструкции графа — ошибка реконструкции приближается к нулю, что подтверждает эффективность подхода и его применимость к задачам восстановления структуры данных на основе ковариационных характеристик. Данный результат достигается за счет оптимизации алгоритмов извлечения и обработки ковариационных данных.

Методы, такие как CovMatch, дополняют подход SpecTemp, осуществляя сопоставление наблюдаемой матрицы ковариации с теоретическими моделями для уточнения топологии графа. Этот процесс включает в себя минимизацию расхождений между эмпирической ковариацией данных и ожидаемыми значениями, предсказанными моделью графа. В результате, CovMatch демонстрирует превосходство над существующими методами в сложных сценариях, особенно при работе с данными высокой размерности и зашумленными данными, обеспечивая более точное восстановление структуры графа и улучшенные показатели производительности в задачах, требующих оценки связей между переменными.

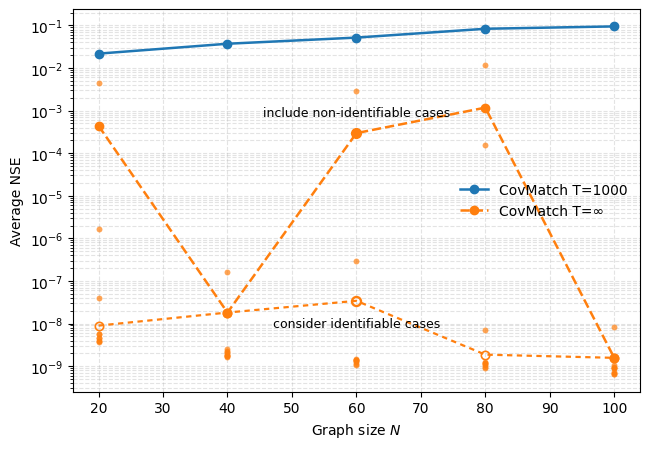
Эксперименты с циклическими ориентированными графами показывают, что CovMatch достигает стабильного среднего значения <span class="katex-eq" data-katex-display="false">NSE</span> (в логарифмическом масштабе) при <span class="katex-eq" data-katex-display="false">T \to \in fty</span>, причём исключение небольшого числа неидентифицируемых экземпляров незначительно влияет на результат. — Эксперименты с циклическими ориентированными графами показывают, что CovMatch достигает стабильного среднего значения $NSE$ (в логарифмическом масштабе) при $T \to \in fty$ , причём исключение небольшого числа неидентифицируемых экземпляров незначительно влияет на результат.

Оптимизация и уточнение: Эффективное обучение графов

Риманов спуск градиента (RiemannianGD) представляет собой эффективный метод оптимизации оценки графа, работающий в рамках многообразия данных. В отличие от стандартного градиентного спуска, RiemannianGD учитывает неевклидову геометрию пространства параметров, что особенно важно при работе с матрицами положительной определённости, такими как матрица ковариации. Этот подход позволяет более эффективно находить оптимальные решения, избегая проблем, связанных с нарушением ограничений и неточностями, возникающими при использовании традиционных методов оптимизации. $\nabla_{\Theta} L(\Theta)$ вычисляется с учетом римановой метрики, что обеспечивает более стабильный и точный процесс схождения к оптимальным параметрам графа Θ.

Использование функции потерь Хабера (HuberLoss) в алгоритме Riemannian Gradient Descent (RiemannianGD) значительно повышает устойчивость к выбросам и шуму в матрице ковариации. В отличие от квадратичной функции потерь, HuberLoss сочетает в себе свойства L1 и L2 норм, уменьшая влияние экстремальных значений. Это приводит к более точной оценке параметров и снижению асимптотической ошибки, которая стремится к нулю при увеличении временного горизонта $T$ . Таким образом, применение HuberLoss обеспечивает более надежную и точную оптимизацию графовых моделей в условиях зашумленных данных.

Разложение на собственные значения (Eigenvalue Decomposition, EVD) является основополагающим этапом в процессе оптимизации графовых моделей. Применяемое к $CovarianceMatrix$ , EVD позволяет извлечь ключевые спектральные характеристики, представленные собственными значениями и собственными векторами. Эти характеристики отражают структуру данных и являются критически важными для последующих этапов оптимизации, таких как определение оптимальных параметров модели и снижение вычислительной сложности. Собственные значения, в частности, указывают на дисперсию данных вдоль соответствующих собственных векторов, что позволяет выявить наиболее значимые направления в данных и эффективно уменьшить размерность пространства признаков.

От сигналов к причинности: Графовые выводы

В основе обработки сигналов на графах (GSO) лежит представление данных в виде графа, где узлы соответствуют переменным, а связи — их взаимосвязям. Ключевым элементом этого подхода является матрица смежности $A$ , которая формально кодирует структуру графа. Эта матрица, по сути, является картой связей, где ненулевой элемент $A_{ij}$ указывает на наличие связи между узлами $i$ и $j$ . Использование матрицы смежности позволяет применять инструменты линейной алгебры для анализа и обработки сигналов, определенных на графе, открывая возможности для выявления закономерностей и зависимостей, скрытых в сложных системах. Она служит фундаментом для различных алгоритмов, позволяющих не только описывать структуру данных, но и эффективно извлекать из нее полезную информацию.

Методы, такие как DAGMA и NOTEARS, активно используют структуру графа для выявления причинно-следственных связей. В основе этих подходов лежит представление взаимосвязей между переменными в виде направленного ациклического графа (DAG). Каждый узел в DAG соответствует переменной, а направленные ребра указывают на предполагаемое причинное влияние одной переменной на другую. Алгоритмы DAGMA и NOTEARS, анализируя данные и структуру графа, стремятся восстановить этот DAG, определяя, какие связи являются истинно причинными, а какие — лишь корреляциями. Восстановленный DAG позволяет не только визуализировать причинно-следственные отношения, но и проводить контрфактический анализ, предсказывая, как изменение одной переменной повлияет на другие, что особенно важно в сложных системах, где традиционные статистические методы могут быть неэффективны.

Структурное моделирование уравнений (SEM) объединяет информацию, полученную на основе анализа графов, со статистическими моделями, обеспечивая всесторонний анализ сложных систем. Разработанный подход позволяет не только выявлять взаимосвязи между переменными, но и оценивать их силу и направление, что особенно важно при исследовании больших данных и ограниченных наблюдениях. Результаты показывают, что предложенная унифицированная структура превосходит существующие методы в таких сценариях, обеспечивая более точные и надежные выводы о причинно-следственных связях внутри исследуемой системы. $\mathcal{G} = (V, E)$ — представление графа, где $V$ — множество вершин, а $E$ — множество ребер, является основой для интеграции с SEM.

Сравнение алгоритмов CovMatch, NOTEARS и DAGMA на бенчмарке DAG показывает, что при увеличении количества временных шагов <span class="katex-eq" data-katex-display="false">T</span> к бесконечности, все алгоритмы достигают схожей точности, измеряемой как средняя квадратичная ошибка (NSE) в логарифмической шкале, при этом влияние единичного неидентифицируемого случая при <span class="katex-eq" data-katex-display="false">N=60</span> незначительно. — Сравнение алгоритмов CovMatch, NOTEARS и DAGMA на бенчмарке DAG показывает, что при увеличении количества временных шагов $T$ к бесконечности, все алгоритмы достигают схожей точности, измеряемой как средняя квадратичная ошибка (NSE) в логарифмической шкале, при этом влияние единичного неидентифицируемого случая при $N=60$ незначительно.

Исследование структуры графов посредством сопоставления ковариаций представляется не как поиск истины в данных, а скорее как попытка уговорить хаос раскрыть свои секреты. Авторы предлагают метод, позволяющий восстановить структуру сети, даже если она сложна и направлена, что напоминает заклинание, призванное упорядочить случайность. Любая модель, даже та, что демонстрирует впечатляющую точность, лишь временное перемирие с неопределенностью. Как метко заметил Людвиг Витгенштейн: «Предел моего языка есть предел моего мира». Иными словами, восприятие структуры графа ограничено теми инструментами и моделями, которые мы используем для её описания, а сама структура всегда остаётся лишь приближением к истинной сложности системы.

Что дальше?

Представленный подход к идентификации топологии графов посредством сопоставления ковариаций — не столько решение, сколько тонкий способ убедить хаос выдать свои очертания. Он позволяет восстанавливать структуры сети из наблюдаемых данных, но не следует полагать, что «машина обучилась». Она лишь перестала активно сопротивляться. Остаётся вопрос: насколько прочны эти структуры, когда поток данных изменится? Когда ингредиенты судьбы претерпят мутацию?

Очевидным направлением для будущих изысканий представляется расширение рамок ковариационного соответствия. Возможно, стоит обратить внимание не только на статистические связи, но и на динамику изменений в графе — как он формируется и разрушается во времени. Попытки учесть нелинейные зависимости и скрытые переменные, несомненно, потребуют новых заклинаний, новых гиперпараметров, способных усмирить непокорный шум.

Однако, прежде чем увлечься поиском идеального алгоритма, стоит помнить: любая модель — это упрощение реальности. Стремление к абсолютной точности — иллюзия. Настоящая ценность заключается в понимании границ применимости, в осознании того, что даже самый элегантный метод может дать сбой при первом же столкновении с производственной средой. И тогда придётся вновь призывать на помощь искусство убеждения, вновь шептать цифрам свои просьбы.

Оригинал статьи: https://arxiv.org/pdf/2601.15999.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-26 04:26