Восстановление скрытых закономерностей: обучение нейронных операторов по неполным данным

Автор: Денис Аветисян

Новый подход позволяет эффективно решать уравнения в частных производных, используя лишь частичные наблюдения и моделирование скрытого пространства.

🐢

Ищешь ракеты? Это не к нам. У нас тут скучный, медленный, но надёжный, как швейцарские часы, фундаментальный анализ.

Бесплатный Телеграм канал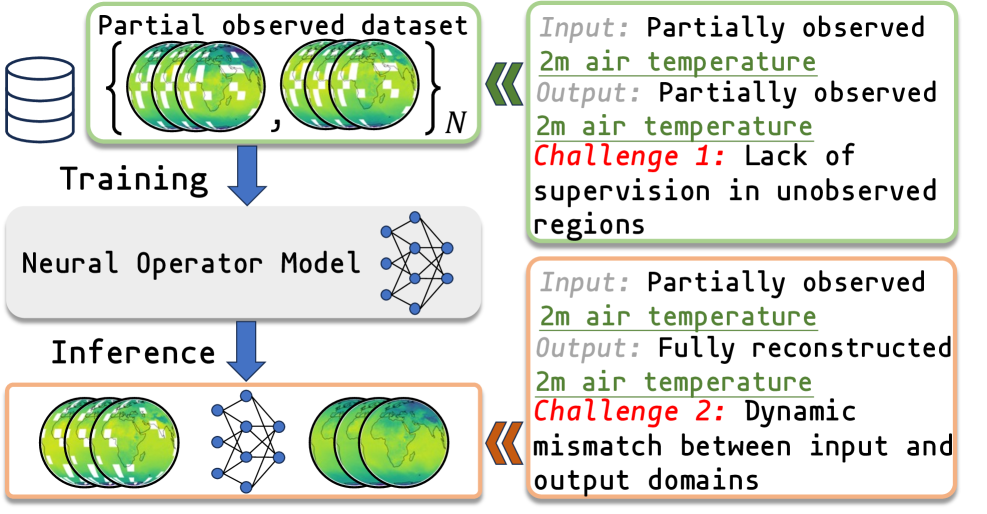

Обучение нейронного оператора при работе с частично наблюдаемыми данными уравнений в частных производных позволяет модели предсказывать решения на основе неполных входных данных, однако данная задача сопряжена с двумя ключевыми трудностями, определяющими эффективность и надежность предсказаний.

Представлен фреймворк LANO, сочетающий маскированное предсказание и авторегрессионную модель для обучения нейронных операторов по неполным данным.

Неполнота наблюдаемых данных является серьезным препятствием для применения современных методов решения уравнений в частных производных в реальных научных задачах. В данной работе, ‘Learning Neural Operators from Partial Observations via Latent Autoregressive Modeling’, предложен новый подход к обучению нейронных операторов на основе неполных наблюдений, сочетающий стратегию маскированного обучения и физически обоснованную авторегрессионную модель в латентном пространстве. Разработанный фреймворк LANO демонстрирует значительное улучшение точности решения задач, связанных с $\mathcal{PDE}$ , в условиях частичной наблюдаемости, достигая снижения относительной ошибки L2 на 18-69% на специализированном бенчмарке POBench-PDE. Сможет ли предложенный подход преодолеть разрыв между идеализированными исследовательскими условиями и сложностями реальных научных вычислений, особенно в задачах с высоким процентом пропущенных данных?

Пророчество Частичной Информации

Многие явления окружающего мира успешно моделируются с помощью уравнений в частных производных (УЧП), которые играют фундаментальную роль в симуляции процессов в физике и инженерии. От прогнозирования погоды и распространения тепла до анализа деформации материалов и динамики жидкостей — УЧП позволяют описывать эволюцию систем во времени и пространстве. $\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2}$ — типичный пример УЧП, описывающий уравнение теплопроводности, где $u$ представляет температуру, а α — коэффициент теплопроводности. Благодаря своей универсальности, УЧП являются незаменимым инструментом для разработки и оптимизации сложных технических систем, а также для проведения научных исследований в различных областях знания. Их применение позволяет создавать виртуальные прототипы, предсказывать поведение систем в экстремальных условиях и разрабатывать новые технологии.

В реальности, сбор полных данных для уравнений в частных производных (УЧП) зачастую является невозможной задачей. Это связано с различными факторами: техническими ограничениями сенсоров, экономической нецелесообразностью проведения измерений во всех точках пространства, или же физической недоступностью определенных областей. В результате, исследователи и инженеры сталкиваются с ситуациями частичного наблюдения, когда информация о решении УЧП известна лишь на ограниченной части границы или внутри рассматриваемой области. Такие сценарии существенно усложняют задачу определения решения, поскольку стандартные численные методы, разработанные для полных данных, оказываются неэффективными или приводят к неустойчивым и неточным результатам. Поэтому, разработка алгоритмов, способных эффективно работать с неполной информацией, является ключевой проблемой в моделировании широкого спектра явлений, от распространения тепла и гидродинамики жидкостей до электромагнитных процессов и прогнозирования погоды.

Традиционные численные методы решения уравнений в частных производных (УЧП), несмотря на свою эффективность в идеальных условиях, демонстрируют значительные трудности при работе с неполными данными. Недостаток информации о начальных или граничных условиях приводит к тому, что алгоритмы, разработанные для полных данных, либо выдают неточные решения, существенно отклоняющиеся от реального поведения системы, либо становятся неустойчивыми, генерируя нефизичные и быстро растущие погрешности. Это особенно критично в задачах моделирования сложных процессов, где даже небольшие ошибки могут накапливаться и приводить к непредсказуемым результатам, препятствуя надежному прогнозированию и управлению динамическими системами. Таким образом, разработка методов, способных эффективно обрабатывать частичные наблюдения и обеспечивать стабильные и точные решения УЧП, является ключевой задачей современной прикладной математики и инженерии.

Предложенная архитектура LANO использует маскированное предсказание следующего кадра (<span class="katex-eq" data-katex-display="false">MPT</span>) на основе траекторий, полученных из частичных наблюдений, и включает в себя новый физически обоснованный латентный прогностик (<span class="katex-eq" data-katex-display="false">PhLP</span>), реализующий гранично-ориентированный авторегрессионный подход. — Предложенная архитектура LANO использует маскированное предсказание следующего кадра ( $MPT$ ) на основе траекторий, полученных из частичных наблюдений, и включает в себя новый физически обоснованный латентный прогностик ( $PhLP$ ), реализующий гранично-ориентированный авторегрессионный подход.

Нейронные Операторы: Новый Взгляд на Моделирование

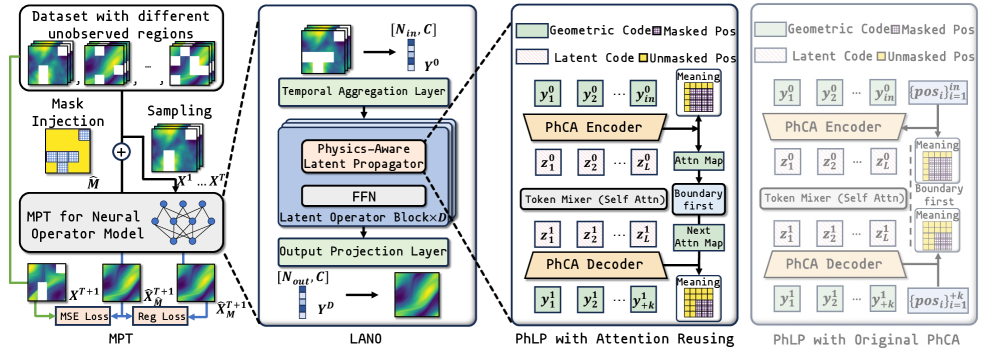
Нейронные операторы представляют собой альтернативный подход к решению задач, основанный на обучении отображению между функциями, заданными на входном и выходном пространствах, непосредственно из данных. В отличие от традиционных методов, требующих явной дискретизации пространства для представления функций, нейронные операторы позволяют избежать этого шага, что снижает вычислительные затраты и упрощает процесс моделирования. Этот подход позволяет обучать модель, которая аппроксимирует решение $u(x)$ на основе входных данных $f(x)$ без необходимости задавать сетку или использовать численные схемы для решения дифференциальных уравнений. Обучение происходит путем минимизации ошибки между предсказанным и истинным решением на наборе обучающих данных, что позволяет модели обобщать решение для новых входных данных без повторной дискретизации.

Нейронные операторы особенно эффективны при решении уравнений в частных производных (УЧП), поскольку позволяют неявно учитывать базовую физику задачи без значительных вычислительных затрат. Традиционные численные методы требуют дискретизации области решения, что приводит к увеличению объема вычислений и потенциальной потере точности. В отличие от них, нейронные операторы обучаются непосредственно на отображении между функциями, представляющими входные и выходные данные УЧП, что позволяет аппроксимировать решение без явного построения сетки. Это приводит к снижению вычислительной сложности и возможности решения задач, требующих высокой точности и скорости, особенно в задачах обратной задачи и оптимизации параметров УЧП. Такой подход позволяет эффективно работать с высокоразмерными данными и сложными граничными условиями, что делает нейронные операторы перспективным инструментом для моделирования различных физических явлений.

Архитектуры, такие как DeepONet, LNO и Transolver, представляют собой значительные достижения в разработке нейронных операторов. DeepONet использует архитектуру на основе слоев внимания для эффективного моделирования нелинейных взаимодействий между входными и выходными функциями. LNO (Linear Neural Operator) применяет свертки в частотной области для обеспечения линейности и эффективности вычислений, что особенно важно для решения задач с высокой размерностью. Transolver, в свою очередь, использует подход, основанный на трансформаторах, позволяя эффективно моделировать глобальные зависимости в данных и обеспечивая высокую точность при решении сложных задач, например, в области гидродинамики. Каждая из этих архитектур обладает уникальными преимуществами в зависимости от специфики решаемой задачи и структуры данных, что делает их ценными инструментами в арсенале исследователей и инженеров.

Несмотря на потерю до 25% данных, модель LANO демонстрирует производительность, сопоставимую или превосходящую результаты основополагающей работы FNO(2020), обеспечивая стабильное улучшение на 18.5-25.0% по сравнению с LNO(2024) в задачах моделирования уравнений Навье-Стокса.

Обучение в Условиях Неопределенности: Устойчивость через Неполноту

Обучение нейронных операторов на неполных данных является критически важным для обеспечения устойчивости и точности прогнозов в реальных приложениях. Неполнота данных — распространенное явление в различных областях, таких как медицинская визуализация, обработка изображений со спутников и мониторинг окружающей среды. Модели, обученные исключительно на полных наборах данных, часто демонстрируют значительное снижение производительности при столкновении с неполными наблюдениями. Использование неполных данных в процессе обучения позволяет модели выучить более надежные представления, устойчивые к пропущенным значениям, что существенно повышает ее обобщающую способность и надежность в условиях реального мира.

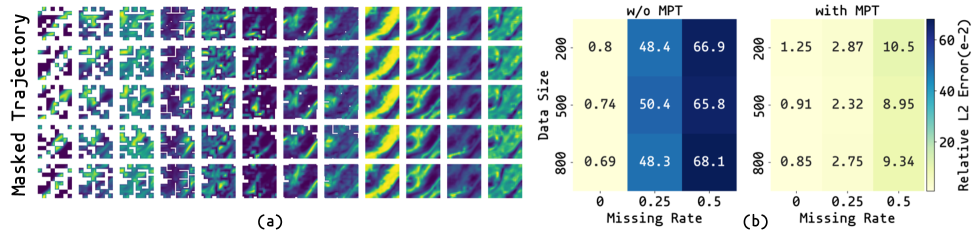
Стратегия Mask-to-Predict Training (MPT) заключается в искусственном создании пропусков в данных на этапе обучения нейронных операторов. В процессе обучения модели получают частично неполные входные данные, что вынуждает их формировать представления, устойчивые к неполным наблюдениям. MPT предполагает маскирование части входных данных и последующее предсказание скрытых значений, тем самым стимулируя модель к извлечению более надежных и общих признаков, не зависящих от полноты входных данных. Это позволяет значительно повысить робастность и точность прогнозов в реальных сценариях, где неполные данные являются распространенным явлением.

Метод Mask-to-Predict Training (MPT) демонстрирует улучшение обобщающей способности моделей на наборах данных с различными типами пропусков. В частности, при использовании MPT на данных с точечными пропусками (Point-wise Missingness) и блочными пропусками (Patch-wise Missingness) наблюдается снижение ошибки до 84.3% при уровне пропусков 50% и размере выборки 200 образцов. Данный результат указывает на эффективность MPT в обучении моделей, устойчивых к неполным данным и способных к точным прогнозам даже при значительной потере информации.

Визуализация распространения скрытых состояний в PhLP демонстрирует, как последовательное углубление слоев позволяет реконструировать траектории из неполных наблюдений, а применение стратегии Mask-to-Predict Training (MPT) значительно снижает погрешность восстановления данных в задачах диффузии-реакции, особенно при большом объеме пропущенных данных.

Стандартизация Оценки: Бенчмаркинг для Сложных Систем

Разработанный комплекс POBench-PDE представляет собой специализированный набор тестов, предназначенный для оценки эффективности решателей уравнений в частных производных (УЧП) в условиях частичного наблюдения. Данный комплекс обеспечивает стандартизированную и воспроизводимую среду тестирования, что критически важно для объективной оценки различных алгоритмов и методов. В отличие от существующих подходов, часто зависящих от конкретных реализаций и данных, POBench-PDE позволяет исследователям сравнивать производительность решателей УЧП в контролируемых условиях, устраняя влияние внешних факторов и обеспечивая надежные результаты. Такая стандартизация способствует более быстрому прогрессу в области численного моделирования и позволяет сосредоточиться на разработке более эффективных и надежных алгоритмов для решения сложных задач, возникающих в различных областях науки и техники.

В рамках разработанного инструментария POBench-PDE для оценки решателей уравнений в частных производных используются реалистичные сценарии, основанные на уравнениях Навье-Стокса и диффузионно-реакционных уравнениях. Эти уравнения широко применяются для моделирования сложных физических явлений, таких как динамика жидкости и перенос веществ. Уравнение Навье-Стокса $\nabla \cdot \mathbf{\sigma} + \mathbf{f} = 0$ описывает движение вязких жидкостей, в то время как диффузионно-реакционные уравнения моделируют процессы, включающие перенос вещества и химические реакции. Использование этих уравнений в качестве основы для бенчмарков позволяет адекватно оценить производительность решателей в задачах, близких к реальным, например, при моделировании потоков в трубопроводах, атмосферных процессов или химических реакторов. Такой подход позволяет выявить сильные и слабые стороны различных алгоритмов и способствует разработке более эффективных и надежных методов решения сложных задач гидродинамики и химического транспорта.

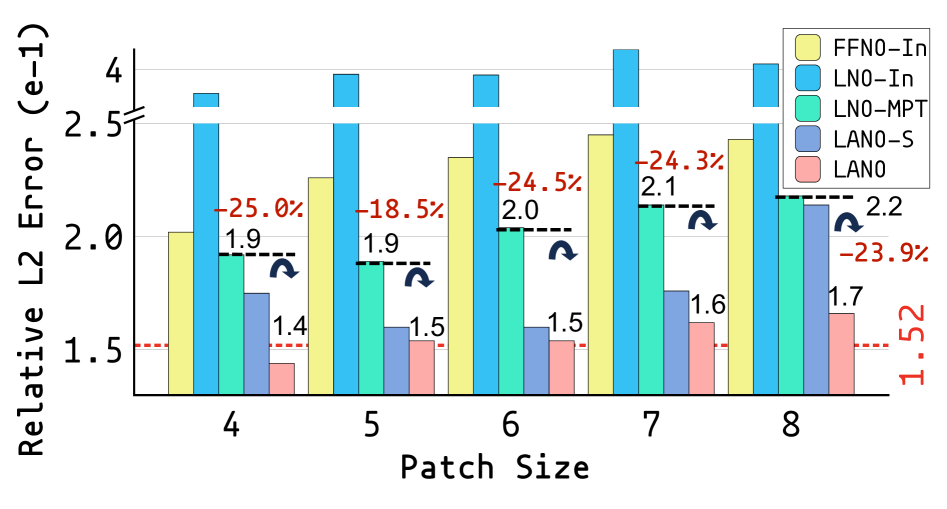
Разработанный фреймворк LANO демонстрирует значительное повышение точности при решении задач, описываемых уравнениями в частных производных (УЧП) при неполных наблюдениях. Исследования показали, что применение LANO позволяет снизить относительную ошибку до 68.7% по сравнению с существующими методами. Более того, фреймворк стабильно превосходит ближайший по эффективности аналог на 17.8%, что подтверждает перспективность использования нейронных операторов и надежных стратегий обучения для решения сложных задач, возникающих в реальных приложениях, таких как гидродинамика и транспорт химических веществ. Такой прогресс открывает новые возможности для моделирования и прогнозирования в различных областях науки и техники, где неполнота данных является распространенной проблемой.

Исследование демонстрирует, что попытки создания всеобъемлющих моделей, решающих уравнения в частных производных, часто сталкиваются с ограничениями неполных данных. Авторы предлагают подход, в котором модель не пытается восстановить недостающую информацию напрямую, а учится предсказывать её развитие во времени, используя латентное пространство и авторегрессивное моделирование. Это напоминает о словах Дональда Дэвиса: «Системы — это не инструменты, а экосистемы. Их нельзя построить, только вырастить». Вместо жёсткой конструкции, стремящейся к идеальной точности, предлагается позволить системе развиваться, адаптироваться и учиться на неполных данных, подобно тому, как растёт сложная экосистема. Акцент на предсказании развития, а не на мгновенном восстановлении, позволяет обойти ограничения, связанные с неполными наблюдениями, и приблизиться к созданию более устойчивой и гибкой системы.

Куда же дальше?

Представленная работа, как и любая попытка обуздать хаос дифференциальных уравнений, скорее раскрывает пропасти незнания, чем заполняет их. Обучение операторов из неполных данных — это не решение, а лишь искусно завуалированное признание собственной неспособности видеть систему целиком. Модель LANO, безусловно, демонстрирует способность к экстраполяции, но каждая успешная предсказание — это лишь отсрочка неминуемого столкновения с реальностью, где данные всегда будут неполными, зашумленными и противоречивыми.

Будущее, вероятно, лежит не в усложнении архитектур, а в принятии принципиальной неопределенности. Вместо того чтобы стремиться к построению «идеального» оператора, стоит сосредоточиться на разработке систем, способных к самовосстановлению и адаптации к новым, непредсказуемым условиям. Представьте себе модель, которая не просто предсказывает, а ожидает ошибку, и заранее подготавливает план её смягчения. Это уже не наука о предсказании, а искусство управления неизбежным.

В конечном счете, вся эта работа — лишь напоминание о том, что системы — это не инструменты, а экосистемы. Их нельзя построить, только взрастить. И каждый архитектурный выбор — это пророчество о будущем сбое. Остается лишь надеяться, что этот сбой будет достаточно элегантным.

Оригинал статьи: https://arxiv.org/pdf/2601.15547.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-24 20:18