Предвидение в языковых моделях: новый взгляд на генерацию текста

Автор: Денис Аветисян

Исследователи предлагают принципиально новый подход к декодированию больших языковых моделей, основанный на теории мартингейлов, для повышения эффективности и надёжности генерации.

☕️

Читаем отчёты, пьём кофе, ждём дивиденды. Если тебе надоел хайп и ты ищешь скучную, но стабильную гавань — добро пожаловать.

Бесплатный Телеграм канал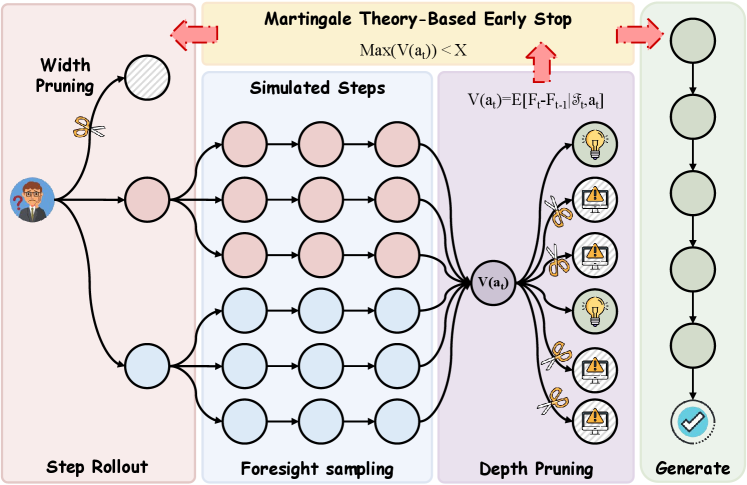

Предложенный алгоритм MFS демонстрирует принципиальную схему прогнозирующего декодирования, визуализированную в рамках одного шага с использованием ширины луча, равной трем, и тремя итерациями развертки, что позволяет эффективно планировать действия.

В статье представлена методика Foresight Sampling, использующая концепции оптимальной остановки и разложения Дуба для улучшения процесса декодирования.

Авторегрессионное декодирование в больших языковых моделях (LLM) зачастую страдает от недальновидности, упуская глобально оптимальные пути рассуждений из-за пошаговой генерации. В настоящей работе, озаглавленной ‘Martingale Foresight Sampling: A Principled Approach to Inference-Time LLM Decoding’, предложен принципиально новый подход, основанный на теории мартингалов, рассматривающий задачу декодирования как идентификацию оптимального стохастического процесса. Этот метод заменяет эвристические механизмы принципами теории вероятностей, используя, в частности, теорему Дуба для оценки преимуществ пути и теорию оптимальной остановки для отсеивания неоптимальных кандидатов. Позволит ли такое переосмысление декодирования LLM значительно повысить точность и эффективность рассуждений, открывая новые горизонты в области искусственного интеллекта?

За пределами предсказания токенов: Ограничения современных LLM

Современные большие языковые модели демонстрируют впечатляющую способность предсказывать следующее слово в последовательности, однако, эта сила часто оказывается недостаточной при решении задач, требующих последовательных, многошаговых рассуждений. Несмотря на кажущуюся беглость речи и способность генерировать связные тексты, модели испытывают трудности с планированием и пониманием долгосрочных последствий действий, что ограничивает их возможности в областях, где необходимо логическое мышление и стратегическое предвидение. В то время как модели успешно справляются с задачами, требующими мгновенного ответа, более сложные сценарии, требующие анализа взаимосвязей и построения логических цепочек, часто оказываются им непосильными, что подчеркивает фундаментальное ограничение, присущее текущей архитектуре языковых моделей.

Существенное ограничение современных больших языковых моделей, получившее название «близрукости декодирования», заключается в неспособности к планированию и предвидению долгосрочных последствий. Модели, обученные предсказывать следующее слово в последовательности, демонстрируют трудности в задачах, требующих последовательности действий и учета отдаленных результатов. Вместо того чтобы разрабатывать стратегию и прогнозировать влияние каждого шага, они фокусируются исключительно на непосредственной вероятности следующего токена, что приводит к ошибкам в сложных сценариях, где важна целостная картина и долгосрочная перспектива. Это не недостаток вычислительной мощности, а принципиальное ограничение архитектуры, ориентированной на краткосрочное предсказание, а не на стратегическое планирование и анализ последствий.

Несмотря на то, что метод «пошагового рассуждения» призван смягчить проблему ограниченности больших языковых моделей, он представляет собой лишь поверхностное решение, не затрагивающее фундаментальные архитектурные недостатки. Данный подход, заключающийся в последовательном разложении сложной задачи на более простые шаги, позволяет моделям генерировать более правдоподобные ответы, однако не решает проблему отсутствия у них способности к долгосрочному планированию и предвидению последствий. Фактически, это скорее трюк, маскирующий неспособность модели к истинному рассуждению, и не предполагает принципиальных изменений в способе обработки информации. Для преодоления этой ограниченности необходимы более глубокие архитектурные инновации, позволяющие моделям формировать и поддерживать внутреннее представление о контексте и целях, выходящее за рамки простого предсказания следующего токена.

Мартингейльный подход к ранней остановке, демонстрируемый на примере GSM8K, позволяет эффективно отсекать неперспективные траектории и сокращать генерацию токенов, определяя порог остановки на основе разницы между кандидатами, что обеспечивает баланс между эффективностью и качеством решения.

Рассуждение как поиск: Внедрение дальновидности и древовидного мышления

Метод “Дерево Мысли” развивает принцип пошагового рассуждения, представляя процесс решения задачи как поиск по дереву решений. В отличие от последовательного генерирования одного варианта ответа, данный подход позволяет исследовать несколько возможных путей развития мысли. На каждом шаге алгоритм генерирует множество потенциальных следующих шагов, оценивает их перспективность и выбирает наиболее многообещающие ветви для дальнейшего развития. Это позволяет моделировать различные сценарии и находить оптимальное решение, учитывая множество факторов и альтернатив, что значительно повышает надежность и качество получаемого результата.

Метод “Прогнозирующей выборки” расширяет принцип “Дерева мыслей”, активно оценивая перспективность каждого шага в процессе рассуждений. Вместо простого предсказания следующего токена, система моделирует вероятные исходы, возникающие при реализации каждого потенциального действия. Это достигается путем симуляции нескольких вариантов развития событий, позволяя оценить ценность каждого шага в контексте достижения конечной цели. Оценка производится на основе прогнозируемых результатов, что позволяет выбирать наиболее перспективные пути решения задачи и избегать тупиковых ветвей рассуждений. Фактически, система “заглядывает в будущее”, чтобы определить, какие шаги наиболее вероятно приведут к успеху.

Традиционные языковые модели, как правило, ориентированы на предсказание следующего токена в последовательности, что ограничивает их способность решать сложные задачи, требующие планирования и анализа. Методы, такие как Tree-of-Thought и Foresight, принципиально меняют этот подход, переходя от простого предсказания к активному поиску оптимального пути решения. Вместо генерации последовательности токенов, модель конструирует и оценивает различные варианты развития событий, рассматривая их как узлы в дереве решений. Это позволяет ей не только прогнозировать вероятные исходы, но и выбирать наиболее перспективные направления, что значительно повышает эффективность решения задач, требующих многошагового планирования и анализа последствий.

Математическая основа: Мартингалы и оптимальная остановка

Теория мартингалов предоставляет мощный математический аппарат для анализа и управления стохастической природой декодирования больших языковых моделей (LLM). В контексте LLM, каждый токен, сгенерированный моделью, можно рассматривать как случайную величину. Последовательность этих случайных величин формирует стохастический процесс. Мартингал — это процесс, где математическое ожидание следующего значения, при условии всех предыдущих значений, равно текущему значению. Это свойство позволяет формально описывать и прогнозировать поведение LLM, оценивать вероятность различных путей генерации текста и разрабатывать стратегии для оптимизации процесса декодирования, такие как улучшение методов поиска $Beam Search$ или разработка новых алгоритмов сэмплирования.

Теорема Дуба о разложении позволяет представить стохастический процесс в виде суммы предсказуемой (детерминированной) компоненты и мартингала, представляющего случайную составляющую. Предсказуемая компонента $μ_t$ отражает ожидаемое изменение процесса, известное на момент времени $t$ , в то время как мартингальная часть $M_t$ описывает непредсказуемые колебания. Разделение процесса таким образом упрощает анализ, поскольку предсказуемая часть может быть вычислена напрямую, а мартингальная часть характеризуется нулевым математическим ожиданием, что позволяет оценивать вероятность различных путей и разрабатывать более точные алгоритмы принятия решений, особенно в контексте декодирования языковых моделей.

Теория оптимальной остановки позволяет разработать принципиальный метод отсечения неоптимальных путей при использовании алгоритма ‘Beam Search’, что повышает эффективность процесса декодирования. В рамках данного подхода, каждый шаг ‘Beam Search’ рассматривается как потенциальная точка остановки. Применяя критерии, основанные на ожидаемой будущей награде (например, вероятности последовательности), можно определить, является ли продолжение текущего пути выгодным. Если ожидаемая награда ниже определенного порога, путь отсекается, освобождая вычислительные ресурсы и фокусируясь на более перспективных вариантах. Это позволяет существенно сократить время декодирования и снизить потребление памяти без значительной потери качества генерируемого текста. $E[X_T | \mathcal{F}_t] \ge X_t$ — ключевое неравенство, определяющее оптимальность остановки в момент времени t.

MFS: Мартингальное прогностическое сэмплирование в действии

Алгоритм MFS (Martingale Foresight Sampling) представляет собой практическую реализацию теоретической основы, объединяющей прогностические возможности с математической строгостью теории мартингалов. В его основе лежит принцип оценки и отсеивания путей поиска на основе вероятностной модели, использующей концепцию ‘предсказуемого преимущества’. Применение теории мартингалов обеспечивает математическую гарантию сходимости алгоритма к оптимальному решению, поскольку позволяет отслеживать кумулятивное вознаграждение или ‘дефицит’ на каждом шаге поиска, что, в свою очередь, позволяет эффективно управлять процессом принятия решений и избегать неперспективных направлений. Это позволяет MFS динамически оценивать перспективность различных путей рассуждений и, таким образом, повышать эффективность поиска оптимального решения.

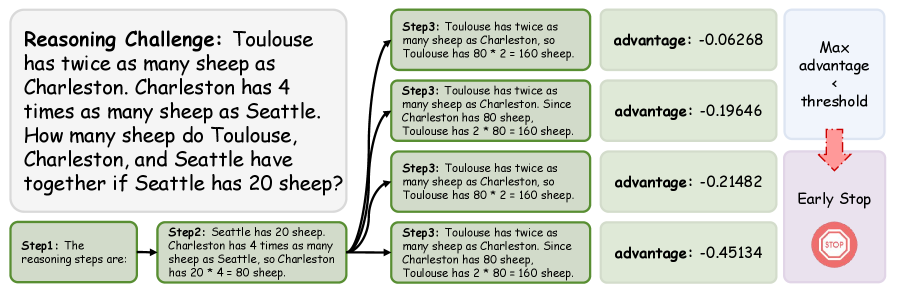
Алгоритм MFS (Martingale Foresight Sampling) использует понятия ‘Предсказуемого Преимущества’ и ‘Процесса Дефицита’ для динамической оценки и отсечения путей поиска. Экспериментальные данные показывают, что для корректных путей рассуждений предсказуемое преимущество находится в диапазоне от -0.458 до -0.458, в то время как для некорректных путей этот показатель составляет от -1.027 до -1.027. Данная разница позволяет алгоритму эффективно выделять перспективные пути и отбрасывать заведомо ложные, оптимизируя процесс поиска оптимального решения.

Теорема о сходимости Мартингала гарантирует сходимость алгоритма к оптимальному решению, обеспечивая надежность его работы. Подтверждением этого служит наблюдение, что правильные пути рассуждений демонстрируют значительно меньшую дисперсию значений шагов (0.249) по сравнению с ошибочными путями (0.994). Низкая дисперсия на корректных путях указывает на предсказуемость и стабильность процесса принятия решений, в то время как высокая дисперсия на ошибочных путях свидетельствует о непредсказуемости и вероятности отклонения от оптимального решения. Это различие в дисперсии является ключевым показателем эффективности алгоритма в выявлении и выборе наиболее перспективных путей рассуждений.

За пределами текущих ограничений: Будущее принципиального рассуждения

Метод Формального Прогнозирования (MFS) значительно расширяет возможности логического мышления больших языковых моделей (LLM) за счет объединения прогностических способностей с надежной математической базой. Вместо простой генерации текста, MFS позволяет LLM предвидеть потенциальные последствия своих действий и оценивать их в рамках четко определенной математической модели. Этот подход позволяет модели не просто отвечать на вопросы, а планировать последовательность шагов для достижения поставленной цели, учитывая возможные препятствия и оптимизируя свои действия. $P(A|B) = \frac{P(B|A)P(A)}{P(B)}$ — подобный расчет вероятностей становится ключевым элементом в процессе принятия решений, что обеспечивает более глубокое и осмысленное взаимодействие с информацией. В результате LLM приобретают способность к более сложному и надежному решению задач, приближаясь к уровню человеческого мышления.

В рамках процесса ϕ-Декодирования, разработанные показатели — “Оценка Соответствия” и “Оценка Преимущества” — предоставляют количественную возможность оценки не только логической последовательности, но и качества генерируемых решений. “Оценка Соответствия” определяет, насколько ответ соответствует исходным требованиям и ограничениям задачи, в то время как “Оценка Преимущества” позволяет сравнивать различные решения, выделяя наиболее оптимальное с точки зрения заданных критериев. Данный механизм, основанный на математическом анализе, позволяет отслеживать прогресс в решении сложных задач и выявлять потенциальные ошибки или несоответствия, обеспечивая более надежный и прозрачный процесс рассуждений искусственного интеллекта. $\phi = (A_c, A_p)$ , где $A_c$ — Оценка Соответствия, а $A_p$ — Оценка Преимущества.

Представленный подход знаменует собой принципиальный сдвиг в парадигме искусственного интеллекта, отходя от простого генерирования текста к целенаправленному, основанному на логике рассуждению. Вместо пассивного воспроизведения информации, системы, использующие подобные методы, способны к активному анализу, планированию и достижению поставленных целей. Это открывает перспективы создания более надёжных и заслуживающих доверия ИИ-агентов, способных не только генерировать связный текст, но и обосновывать свои решения, предвидеть последствия и действовать в соответствии с заданными принципами. Подобный переход к целенаправленному рассуждению является ключевым шагом на пути к созданию искусственного интеллекта, который действительно может решать сложные задачи и быть полезным инструментом для человека.

Исследование, представленное в статье, стремится к упрощению процесса декодирования больших языковых моделей, что находит отклик в философии ясности как высшей формы любви. Авторы предлагают подход, основанный на теории мартингалов, стремясь выявить оптимальный стохастический процесс. Это напоминает стремление к удалению всего лишнего, к поиску структуры смысла. Как однажды заметил Дональд Дэвис: «Сложность — это тщеславие. Ясность — милосердие». Использование принципов оптимальной остановки в контексте LLM декодирования демонстрирует стремление к элегантности и эффективности, к минимизации неопределенности и повышению надежности вывода. Подобный подход к декодированию, основанный на математической строгости, позволяет отделить существенное от несущественного, обеспечивая более четкий и осмысленный результат.

Что дальше?

Предложенный подход, опираясь на теорию мартингейлов, не решает проблему неоптимальности декодирования языковых моделей, но переформулирует её. Абстракции стареют, принципы — нет. Идея о поиске оптимальной стохастической процедуры выглядит элегантно, однако, практическая реализация, требующая оценки и управления мартингейльными характеристиками, таит в себе значительные вычислительные издержки. Каждая сложность требует алиби.

Перспективы связаны не с усложнением модели, а с её упрощением. Необходимо исследовать, как принципы оптимальной остановки могут быть применены для динамического отсечения нерелевантных путей декодирования, снижая вычислительную нагрузку без существенной потери качества. Довольно ли эффективна эта стратегия в сценариях, где требуется генерация длинных и сложных текстов?

Ключевым вопросом остаётся оценка субоптимальности. До сих пор неясно, как измерить «упущенную выгоду» от выбора определённой стратегии декодирования. Реальное продвижение потребует не просто улучшения метрик, а понимания фундаментальных ограничений, присущих процессу генерации текста.

Оригинал статьи: https://arxiv.org/pdf/2601.15482.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-24 13:37